
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Произведение комплексных чисел.Содержание книги
Поиск на нашем сайте
Произведением комплексных чисел z1 = a + bi и z2 = c + di называется комплексное число (ac - bd)+(ad + bc)i. Определение произведения устанавливается с таким расчетом, чтобы (a + bi) и (c + di) можно было перемножить как алгебраические двучлены, считая при этом, что i*i = -1. Произведение комплексных чисел обладает свойствами: коммутативности: z1 * z2 = z2 * z1 ассоциативности: (z1 * z2) * z3 = z1 * (z2 * z3) дистрибутивности: z1 * (z2 + z3) = z1 * z2 + z1 * z3 На основании определения произведения комплексных чисел можно определить натуральную степень комплексного числа: zn = z * z *... * z n раз.
Разность комплексных чисел. Разностью комплексных чисел z1 = a + bi и z2 = c + di называется комплексное число z = z1 - z2 = (a - c) + (b - d)i. Частное. Частным от деления комплексного числа z1 на комплексное число z2 называется такое число z, которое удовлетворяет условию z? z2 = z2? z= = z1.
Билет 29. Геометрическое изображение комплексных чисел. Модуль и аргумент.
Действительные числа можно изобразить точками прямой линии, как показано на рисунке, где точка A изображает число 4, а точка B число -5. Эти же числа можно изображать также отрезками OA, OB, учитывая не только их длину, но и направление. Каждая точка M числовой прямой изображает некоторое действительное число (рациональное, если отрезок OM соизмерим с единицей длины, и иррациональное если несоизмерим). Таким образом, на числовой прямой не остается места для комплексных чисел.
Но комплексные числа можно изображать на числовой плоскости. Для этого мы выбираем на плоскости прямоугольную систему координат, с одинаковым масштабом на обеих осях. Комплексное число a + b·i изображается точкой M, у которой абсцисса x равна абсциссе a комплексного числа, а ордината y равна ординате b комплексного числа.
Длина вектора, изображающего комплексное число, называется модулем комплексного числа. Модуль любого комплексного числа, не равного нулю, есть положительное число. Модуль комплексного числа a + b·i обозначается |a + b·i |, а также буквой r. Из чертежа видно, что: Модуль действительного числа, совпадает с его абсолютным значением. Сопряженные комплексные числа a + b·i и a - b·i имеют один и тотже модуль.
Угол φ между осью абсцисс и вектором OM, изображающим комплексное число a + b·i, называется аргументом комплексного числа a + b·i
Каждое не равное нулю комплексное число имеет бесчисленное множество аргументов, отлючающихся друг от друга на целое число полных оборотов (т.е. на 360°·k, где k - любое целое число). Аргумент комплексного числа связан с его координатами следующими формулами:
Однако ни одна из этих формул в отдельности не позволяет найти аргумент. Для того чтобы найти аргумент комплексного числа, эти формулы надо использовать в совокупности, а также учитывать номер четверти, на координатной плоскости, в которой находится комплексное число.
Билет 30. Тригонометрическая форма комплексного числа. Формула Муавра.
Абсцисса a и ордината b комплексного числа a + b·i выражаются через модуль r и аргумент φ формулами:
Поэтому всякое комплексное число можно представить в виде: a+b*i = r*(cos (φ) + i*sin (φ)) Это так называемая, нормальная тригонометрическая форма, или просто, тригонометрическая форма комплексного числа. В противоположность тригонометрической форме выражение вида a + b·i называется алгебраической или координатной формой комплексного числа.
Формула Муавра для комплексных чисел
Формула Муавра сразу следует из формулы Эйлера Открыта французским математиком Абрахамом де Муавро
Билет 31. Корень n-ой степени из комплексного числа. Корнем n -ой степени из комплексного числа называется такое комплексное число, n-я степень которого равна подкоренному числу. Из этого определения следует, что из равенства Из равенства комплексных чисел следует
В этой формуле число k может принимать всевозможные целые значения, но различных значений корня будет только n и они соответствуют значениям k = 0, 1, 2, …, n - 1.
Докажем этот факт. Действительно, правые части в этой формуле различны тогда, когда аргументы
Пусть теперь k3– целое число, не входящее в эту последовательность подряд взятых значений k. Это число можно представить в виде k3= gn + ki, где g – целое число, а ki – одно из чисел этого ряда, поэтому Вывод: корень n -ой степени из комплексного числа имеет n различных значений. Исключением из этого правила является лишь частный случай, когда извлекается корень из нуля. В этом случае все значения корня равны нулю.
Основные определения и задачи линейного программирования. Задачи оптимального планирования, связанные с отысканием оптимума заданной целевой функции (линейной формы) при наличии ограничений в виде линейных уравнений или линейных неравенств относятся к задачам линейного программирования. Линейное программирование - наиболее разработанный и широко применяемый раздел математического программирования. Это объясняется следующим:
Итак, Линейное программирование – это направление математического программирования, изучающее методы решения экстремальных задач, которые характеризуются линейной зависимостью между переменными и линейным критерием. Необходимым условием постановки задачи линейного программирования являются ограничения на наличие ресурсов, величину спроса, производственную мощность предприятия и другие производственные факторы. Сущность линейного программирования состоит в нахождении точек наибольшего или наименьшего значения некоторой функции при определенном наборе ограничений, налагаемых на аргументы и образующих систему ограничений, которая имеет, как правило, бесконечное множество решений. Каждая совокупность значений переменных (аргументов функции F), которые удовлетворяют системе ограничений, называется допустимым планом задачи линейного программирования. Функция F, максимум или минимум которой определяется, называется целевой функцией задачи. Допустимый план, на котором достигается максимум или минимум функции F, называется оптимальным планом задачи. Система ограничений, определяющая множество планов, диктуется условиями производства. Задачей линейного программирования (ЗЛП) является выбор из множества допустимых планов наиболее выгодного (оптимального). В общей постановке задача линейного программирования выглядит следующим образом:
Имеются какие-то переменные х = (х1, х2, … хn) и функция этих переменных f(x) = f (х1, х2, … хn), которая носит название целевой функции. Ставится задача: найти экстремум (максимум или минимум) целевой функции f(x) при условии, что переменные x принадлежат некоторой области G:
В зависимости от вида функции f(x) и области G и различают разделы математического программирования: квадратичное программирование, выпуклое программирование, целочисленное программирование и т.д. Линейное программирование характеризуется тем, что Математическая модель любой задачи линейного программирования включает в себя:
Или
Задачи. Общей задачей линейного программирования называется задача, которая состоит в определении максимального (минимального) значения функции
при условиях
где Определение 2. Функция (8) называется целевой функцией (или линейной формой) задачи (8) – (11), а условия (9) – (11) – ограничениями данной задачи. Определение 3. Стандартной (или симметричной} задачей линейного программирования называется задача, которая состоит в определении максимального значения функции (8) при выполнении условий (9) и (11), где k = m и l = n. Определение 4. Канонической (или основной) задачей линейного программирования называется задача, которая состоит в определении максимального значения функции (8) при выполнении условий (10) и (11), где k = 0 и l = п. Определение 5. Совокупность чисел Определение 6. План Значение целевой функции (8) при плане Х будем обозначать через Указанные выше три формы задачи линейного программирования эквивалентны в том смысле, что каждая из них с помощью несложных преобразований может быть переписана в форме другой задачи. Это означает, что если имеется способ нахождения решения одной из указанных задач, то тем самым может быть определен оптимальный план любой из трех задач.
Чтобы перейти от одной формы записи задачи линейного программирования к другой, нужно уметь, во-первых, сводить задачу минимизации функции к задаче максимизации; во-вторых, переходить от ограничений-неравенств к ограничениям-равенствам и наоборот; в-третьих, заменять переменные, которые не подчинены условию неотрицательности. В том случае, когда требуется найти минимум функции Ограничение-неравенство исходной задачи линейного программирования, имеющее вид “
преобразуется в ограничение-равенство
а ограничение-неравенство
– в ограничение-равенство
В то же время каждое уравнение системы ограничений
можно записать в виде неравенств:
Число вводимых дополнительных неотрицательных переменных при преобразовании ограничений-неравенств в ограничения-равенства равно числу преобразуемых неравенств. Вводимые дополнительные переменные имеют вполне определенный экономический смысл. Так, если в ограничениях исходной задачи линейного программирования отражается расход и наличие производственных ресурсов, то числовое значение дополнительной переменной в плане задачи, записанной в форме основной, равно объему неиспользуемого соответствующего ресурса. Отметим, наконец, что если переменная
Билет 33. Графический метод решения задач линейного программирования. Графический метод основан на геометрической интерпретации задачи линейного программирования и применяется в основном при решении задач двумерного пространства и только некоторых задач трёхмерного пространства, так как довольно трудно построить многогранник решений, который образуется в результате пересечения полупространств. Задачу пространства размерности больше трёх изобразить графически вообще невозможно. Пусть задача линейного программирования задана в двумерном пространстве, то есть ограничения содержат две переменные. Найти минимальное значение функции
При
Допустим, что система (2) при условии (3) совместна и её многоугольник решений ограничен. Каждое из неравенств (2) и (3), как отмечалось выше, определяет полуплоскость с граничными прямыми:
Значения
Алгоритм графического метода решения задач линейного программирования с двумя переменными: 1. Построить область допустимых решений. 2. Если область допустимых решений является пустым множеством, то задача не имеет решения ввиду несовместности системы ограничений. 3. Если область допустимых решений является непустым множеством, построить нормаль линий уровня n = (c1, c2) и одну из линий уровня, имеющую общие точки с этой областью. 4. Линию уровня переместить до опорной прямой в задаче на максимум в направлении нормали, в задаче на минимум - в противоположном направлении. 5. Если при перемещении линии уровня по области допустимых решений в направлении, соответствующем приближению к экстремуму целевой функции, линия уровня уходит в бесконечность, то задача не имеет решения ввиду неограниченности целевой функции. 6. Если задача линейного программирования имеет оптимальное решение, то для его нахождения нужно решить систему уравнений для прямых, ограничивающих область допустимых решений и имеющих общие точки с соответствующей опорной прямой. Если целевая функция задачи достигает максимума (минимума) в двух угловых точках, то задача имеет бесконечное множество решений. Оптимальным решением является любая выпуклая линейная комбинация этих точек.
|
|||||||||
|
Последнее изменение этой страницы: 2019-12-15; просмотров: 213; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.219.81.129 (0.007 с.) |








 , заданная в тригонометрической форме — формула
, заданная в тригонометрической форме — формула
 и правила для экспонент
и правила для экспонент  , верного, если b — целое число. (Если b — не целое, то
, верного, если b — целое число. (Если b — не целое, то  — многозначная функция переменной a и
— многозначная функция переменной a и  — одно из её значений.)
— одно из её значений.) следует равенство
следует равенство  .
. , а аргументы отличаются на число, кратное
, а аргументы отличаются на число, кратное 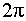 ;. Отсюда
;. Отсюда  ,
,  . Здесь
. Здесь  есть арифметическое значение корня, а k – любое целое число. Таким образом, получается формула
есть арифметическое значение корня, а k – любое целое число. Таким образом, получается формула .
. и
и 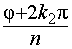 отличаются на величину, не кратную
отличаются на величину, не кратную  не может быть кратна
не может быть кратна  , то есть значению k3 соответствует то же значение корня, что и значению ki.
, то есть значению k3 соответствует то же значение корня, что и значению ki.
 (8)
(8)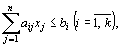 (9)
(9) (10)
(10) (11)
(11) - заданные постоянные величины и
- заданные постоянные величины и  .
. ,удовлетворяющих ограничениям задачи (9) – (11), называется допустимым решением (или планом).
,удовлетворяющих ограничениям задачи (9) – (11), называется допустимым решением (или планом). , при котором целевая функция задачи (8) принимает свое максимальное (минимальное) значение, называется оптимальным.
, при котором целевая функция задачи (8) принимает свое максимальное (минимальное) значение, называется оптимальным. . Следовательно, X*– оптимальный план задачи, если для любого Х выполняется неравенство
. Следовательно, X*– оптимальный план задачи, если для любого Х выполняется неравенство  [соответственно
[соответственно  ].
]. , можно перейти к нахождению максимума функции
, можно перейти к нахождению максимума функции  , поскольку
, поскольку 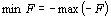 .
. ”, можно преобразовать в ограничение-равенство добавлением к его левой части дополнительной неотрицательной переменной, а ограничение-неравенство вида “
”, можно преобразовать в ограничение-равенство добавлением к его левой части дополнительной неотрицательной переменной, а ограничение-неравенство вида “  ” – в ограничение-равенство вычитанием из его левой части дополнительной неотрицательной переменной. Таким образом, ограничение-неравенство
” – в ограничение-равенство вычитанием из его левой части дополнительной неотрицательной переменной. Таким образом, ограничение-неравенство
 (12)
(12)
 (13)
(13)
 (14)
(14) , не подчинена условию неотрицательности, то ее следует заменить двумя неотрицательными переменными
, не подчинена условию неотрицательности, то ее следует заменить двумя неотрицательными переменными  и
и  , приняв
, приняв  .
.

 . Линейная функция (1) при фиксированных значениях
. Линейная функция (1) при фиксированных значениях  является уравнением прямой линии:
является уравнением прямой линии:  . Построим многоугольник решений системы ограничений (2) и график линейной функции (1) при
. Построим многоугольник решений системы ограничений (2) и график линейной функции (1) при  . Тогда поставленной задаче линейного программирования можно дать следующую интерпретацию. Найти точку многоугольника решений, в которой прямая
. Тогда поставленной задаче линейного программирования можно дать следующую интерпретацию. Найти точку многоугольника решений, в которой прямая  возрастают в направлении вектора
возрастают в направлении вектора  , поэтому прямую
, поэтому прямую  . Прямая дважды становится опорной по отношению к многоугольнику решений (в точках
. Прямая дважды становится опорной по отношению к многоугольнику решений (в точках  и
и  ), причем минимальное значение принимает в точке
), причем минимальное значение принимает в точке  находим, решая систему уравнений прямых
находим, решая систему уравнений прямых  и
и  .
.


