Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Формула для приращения функции. Дифференциал функции.
Формула малых приращений Подставив (2) в (1) и отбросив ω (x - x 0), получаем формулу малых приращений: Δ f (x 0) ≈ df (x 0) или f (x) ≈ f (x 0) + f' (x 0)(x - x 0), (4) позволяющую при малых значениях x - x 0 приближенно вычислять значения функции f в точках x, близких к точке x 0, где значения функции f и ее производной известны.
Формула конечных приращений
Формула конечных приращений или теорема Лагра́нжа о среднем значении утверждает, что если функция
Геометрически это можно переформулировать так: на отрезке Механическое истолкование: Пусть Для функции одной переменной: Введем функцию
Правила дифференцирования функций Если скалярные величины u и v дифференцируемы, то: а) б) в) г) Если вектор-функции u и v дифференцируемы, то а) d (u ± v) = d u ± d v; б) d (u, v) = (d u, v) + (u, d v); в) d (λ u) = u d λ + λ d u (λ - скалярная функция). Если u и v - скалярные дифференцируемые функции, то d (u ± iv) = du ± i dv, i 2 = -1. Если A, B - дифференцируемые матричные функции, u - дифференцируемая вектор-функция, то а) d (A ± B) = dA ± dB; б) d (A u) = (dA) u + A d u; в) d (AB) = (dA) B + A dB.
Инвариантность формы и геометрический смысл первого дифференциала Понятие дифференциала Пусть функция y = f (x) дифференцируема при некотором значении переменной x. Следовательно, в точке x существует конечная производная
Тогда по определению предела функции разность
является бесконечно малой величиной при
(величина Если
оно является бесконечно малой того же порядка малости, что и
Поэтому говорят, что первое слагаемое формулы (2) является главной, линейной относительно
Эту главную часть приращения функции называют дифференциалом данной функции в точке x и обозначают
или
Следовательно,
или
Итак, дифференциал функции y = f (x) равен произведению её производной на приращение независимой переменной. Замечание. Нужно помнить, что если x – исходное значение аргумента,
- наращенное значение, то производная в выражении дифференциала берётся в исходной точке x; в формуле (5) это видно из записи, в формуле (4) – нет. Дифференциал функции можно записать в другой форме:
или
Геометрический смысл дифференциала. Дифференциал функции y = f (x) равен приращению ординаты касательной, проведённой к графику этой функции в точке (x; y), при изменении x на величину
Свойства дифференциала. Инвариантность формы дифференциала В этом и следующем параграфах каждую из функций будем считать дифференцируемой при всех рассматриваемых значениях её аргументов. Дифференциал обладает свойствами, аналогичными свойствам производной:
Формулы (8) – (12) получаются из соответствующих формул для производной умножением обеих частей каждого равенства на Рассмотрим дифференциал сложной функции. Пусть
Дифференциал
этой функции, используя формулу для производной сложной функции, можно записать в виде
Но
т.е.
Здесь дифференциал записан в том же виде, как и в формуле (7), хотя аргумент
Подчеркнём, что в формуле (13) нельзя заменить
для любой функции
|
||||||
|
Последнее изменение этой страницы: 2019-12-15; просмотров: 349; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.139.72.78 (0.015 с.) |

 непрерывна на отрезке
непрерывна на отрезке  и дифференцируема в интервале
и дифференцируема в интервале  , то найдётся такая точка
, то найдётся такая точка 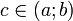 , что
, что .
.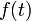 — расстояние точки в момент
— расстояние точки в момент  от начального положения. Тогда
от начального положения. Тогда  есть путь, пройденный с момента
есть путь, пройденный с момента  до момента
до момента 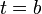 , отношение
, отношение  — средняя скорость за этот промежуток.
— средняя скорость за этот промежуток. . Для нее выполнены условия теоремы Ролля: на концах отрезка ее значения равны
. Для нее выполнены условия теоремы Ролля: на концах отрезка ее значения равны 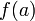 . Воспользовавшись упомянутой теоремой, получим, что существует точка
. Воспользовавшись упомянутой теоремой, получим, что существует точка  , в которой производная функции
, в которой производная функции  равна нулю:
равна нулю:

 ;
;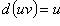
 ;
;
 ;
;
 ;
;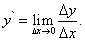
 (1)
(1)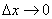 . Выразив из равенства (1) приращение функции, получим
. Выразив из равенства (1) приращение функции, получим (2)
(2) не зависит от
не зависит от  , т. е. остаётся постоянной при
, т. е. остаётся постоянной при  , то в правой части равенства (2) первое слагаемое
, то в правой части равенства (2) первое слагаемое  линейно относительно
линейно относительно  - бесконечно малая более высокого порядка малости, чем первое, так как их отношение
- бесконечно малая более высокого порядка малости, чем первое, так как их отношение  стремится к нулю при
стремится к нулю при
 (3)
(3)

 (4)
(4) (5)
(5)
 (6)
(6)
 .
. (С – постоянная величина) (8)
(С – постоянная величина) (8) (9)
(9) (10)
(10) (11)
(11) (12)
(12) .
. - сложная функция
- сложная функция 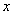 :
:

 есть дифференциал функции
есть дифференциал функции  , поэтому
, поэтому ,
, (13)
(13) на
на  , так как
, так как