
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Вопрос. Направление вогнутости. Точки перегиба.Содержание книги
Поиск на нашем сайте
Пустьфункция f (x)дваждыдифференцируема(имеет вторую производную) наинтервале (a, b), тогда: если f'' (x)>0 для любого x если f'' (x)<0 для любого x Точка,припереходе через которую функция меняет выпуклость на вогнутость или наоборот, называется точкойперегиба. Отсюда следует,чтоесли в точкеперегиба x 0существует вторая производная f'' (x 0), то f'' (x 0) = 0. Дифференцируемая функция называется выпуклой вниз на интервале Х, если ее график расположен не ниже касательной к нему в любой точке интервала Х.
Билет 57. Правило Лопиталя. Правило Лопиталя представляет собой метод вычисления пределов, имеющих неопределенность типа
Пусть a является некоторым конечным действительным числом или равно бесконечности. - Если - Если
Правило Лопиталя можно также применять к неопределенностям типа Правило Лопиталя справедливо также и для односторонних пределов.
Билет 58. Формулы Тейлора и Маклорена. Разложение функций в степенные ряды.
Пусть функция f(x) определена на интервале (а; b) и имеет в точке х0 Разложение функций в степенной ряд имеет большое значение для решения различных задач исследования функций, дифференцирования, интегрирования, решения дифференциальных уравнений, вычисления пределов, вычисления приближенных значений функции. Возможны различные способы разложения функции в степенной ряд. Такие способы как разложение при помощи рядов Тейлора и Маклорена были рассмотрены ранее. Существует также способ разложения в степенной ряд при помощи алгебраического деления. Это – самый простой способ разложения, однако, пригоден он только для разложения в ряд алгебраических дробей.
59. Функции спроса и предложения. Равновесная цена и равновесный объем. Закон спроса устанавливает, что существует отрицательная связь между количеством какого-либо блага, которые люди будут покупать, и ценой, т. е. при более высоких ценах купят меньше, при более низких больше. Следовательно, тангенс угла наклона графика спроса будет отрицательным. Функция предложения (закон предложения) – соотношение между ценой и количеством товара, выставленного на продажу. Закон предложения устанавливает, что существует положительная связь между количеством товара и ценой. Следовательно, тенгенс угла наклона графика предложения положителен. В простейшем случае эти функции линейны. Закон спроса обозначен через D, закон предложения – через S, x – количество товара, p – цена на этот товар. Уравнение спроса можно составить, если заданы две точки, лежащие на его графике. Для этого нужно использовать уравнение прямой, проходящей через две заданные точки: р-р1=(р2-р1/х2-х1)(х-х1) Точка пересечения кривых спроса и предложения (х0, р0) наз. точкой рыночного равновесия. Соответственно р0 называется равновесной ценой, а х0 – равновесным количеством (объемом продаж). Рассмотрим, что происходит с графиками спроса и предложения в случае, если правительство вводит налог t или предоставляют субсидию s. При использовании линейных моделей предполагается, что спрос определяется только ценой товара на рынке рD, а предложение - только ценой рS, получаемой поставщиками. Эти цены связаны между собой следующими уравнениями: pD=pS+t; PD=pS-s где t и s – соответственно налог и субсидия на единицу товара. Т. о. при введении налога или субсидии уравнение спроса D не изменится. График фнкции предложения поднимется на t единиц вверх или опустится на s единиц вниз. Вместо субсидии иногда вводится минимальная цена. В этом случае правительство скупает излишек продукции, равный хS -хD. Некоторые налоги, например НДС, пропорциональны цене. В этом случае остается той же точка пересечения графика предложения с осью Ох и меняется угол наклона графика к оси Ох. Точка рыночного равновесия наз. устойчивой, если при малых отклонениях от равновесного значения цена стремится к этому равновесному значению. Пусть р > р0, тогда хS > xD. Поскольку предложение превышает спрос, то цена падает и р→р0. Если р < р0, то хS < < xD. Поскольку спрос превышает предложение, то цена растет и р → р0. Следовательно точка рыночного равновесия устойчива.
Билет 60. Функции многих переменных в экономике. Производственные функции. Изокванта.
В экономике часто рассматривается и используется многофакторные функции, или функции нескольких переменных. Например, производственные функции, в которых независимых переменных бывает несколько. производственные функции описывают взаимосвязь между объектами вовлечения и получения благ в ходе деятельности предприятия. Часто вовлекаемые блага называются факторами производства, «вход» или исходными продуктами. К выпускаемым благам относятся полуфабрикаты и готовые изделия, промежуточная и готовая продукция, они называются выпуском продукции или «выход» Например, производственная функция Кобба-Дугласа имеет вид: Y= Y0* Kα * L1- α, где Y – величина общественного продукта L – затраты труда K – объём производственных фондов Y0 и α – постоянные – 0<α<1 K и L – аргументы, Y – функция двух переменных..
Изокванта - кривая, демонстрирующая различные варианты комбинаций факторов производства, которые могут быть использованы для выпуска данного объема продукта. Изокванты иначе называют кривыми равных продуктов, или линиями равного выпуска. Наклон изокванты выражает зависимость одного фактора от другого в производственном процессе. При этом увеличение одного фактора и уменьшение другого не вызывает изменений в объеме выпускаемой продукции.
Положительный наклон изокванты означает, что увеличение применения одного фактора потребует увеличения применения другого фактора, чтобы не сократить выпуск продукции. Отрицательный наклон изокванты показывает, что сокращение одного фактора (при определенном объеме производства) всегда будет вызывать увеличение другого фактора.
Кривизна изокванты иллюстрирует эластичность замещения факторов при выпуске заданного объема продукта и отражает то, насколько легко один фактор может быть заменен другим. В том случае, когда изокванта похожа на прямой угол, вероятность замещения одного фактора другим крайне невелика. Если же изокванта имеет вид прямой линии с наклоном вниз, то вероятность замены одного фактора другим значительна.
Билет 61. Предел и непрерывность функции многих переменных.
1. Постоянное число А называется пределом функции f(x) при x®a, если для всякой последовательности {xn} значений аргумента, стремящейся к а, соответствующие им последовательности {f(xn)} имеют один и тот же предел А. Это определение называют определением предела функции по Гейне, или “ на языке последовательностей ”. 2. Постоянное число А называется пределом функции f(x) при x®a, если, задав произвольное как угодно малое положительное число e, можно найти такое d >0 (зависящее от e), что для всех x, лежащих в d-окрестности числа а, т.е. для x, удовлетворяющих неравенству Это определение называют определением предела функции по Коши, или “на языке e - d“. Функция f(x) называется непрерывной справа в точке xo, если
и непрерывной слева в точке xo, если
Непрерывность функции в точке xo равносильна ее непрерывности в этой точке одновременно и справа и слева 62 56. Коэффициенты эластичности функции многих переменных. В экономике очень часто вместо обычной производной используется так называемая относительная производная, или эластичность, которая для функции у=f(х) определяется и обозначается следующим образом: Ex(y)=lim∆x→0(∆y/∆x)*x/y Для обозначения эластичности функции у=f(х) существуют и другие символы: Еух(х), Еу(х), εf(x), Elxf(x), Elxy. Используя определение производной, эластичность можно задать формулой: Eх(у)=у’ * x/y Говорят также, что Eх(у) – это коэффициент эластичности у по х. Понятие эластичности было введено Аланом Маршаллом в связи с анализом функции спроса. Это понятие может применятся при анализе любых дифференцируемых функций. Из определения эластичности вытекает, что при достаточно малых ∆x выполняется приближенное равенство ∆y/у≈ Eх(у)* ∆x/х Отсюда следует, что эластичность Eх(у) – это коэффициент пропорциональности между относительными изменениями величин у и х. Если например х увеличивается на 1 %, то у увеличивается (уменьшается) приблизительно на Eх(у) процентов. Эластичность в экономике используется достаточно часто еще и потому, что эта величина является безразмерной и не зависит от выбора единиц измерения величин у и х. Это утверждение следует из безразмерности и независимости от выбора единиц измерения отношений ∆y/у, ∆x/х.
63 Дифференциал ф-иимногих переменных
|
|||||||
|
Последнее изменение этой страницы: 2019-12-15; просмотров: 206; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.145.73.167 (0.007 с.) |

 (a, b),тофункция f (x) является вогнутой наинтервале (a, b);
(a, b),тофункция f (x) является вогнутой наинтервале (a, b); или
или  .
. и
и  , то
, то 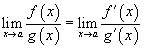 ;
;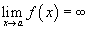 и
и  , то аналогично
, то аналогично  . Первые две неопределенности
. Первые две неопределенности  можно свести к типу
можно свести к типу  сводятся к типу
сводятся к типу  с помощью соотношения
с помощью соотношения
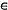 (а; b)
(а; b) 



 ,
, .
. Если Δz представлено в виде:
Если Δz представлено в виде:
 где A, B - постоянные (не зависящие от Δx, Δy),
где A, B - постоянные (не зависящие от Δx, Δy),  - расстояние между M и M0, α(Δ x,Δy) - бесконечно малая при Δx
- расстояние между M и M0, α(Δ x,Δy) - бесконечно малая при Δx  0, Δy
0, Δy  называется полным дифференциалом функции z =f(х;у) в точке M0.
Теорема 1.1. Если z =f(х;у) дифференцируема в точке M0, то
называется полным дифференциалом функции z =f(х;у) в точке M0.
Теорема 1.1. Если z =f(х;у) дифференцируема в точке M0, то
 Доказательство
Так как в (1.16) Δx, Δy - произвольные бесконечно малые, то можно взять Δy =0, Δx≠0, Δx
Доказательство
Так как в (1.16) Δx, Δy - произвольные бесконечно малые, то можно взять Δy =0, Δx≠0, Δx  после чего из (1.16) следует
после чего из (1.16) следует
 Тогда
Тогда
 Аналогично доказывается, что
Аналогично доказывается, что
 и теорема 1.1. доказана.
Замечание: из дифференцируемости z =f(х,у) в точке M0 следует существование частных производных. Обратное утверждение неверно (из существования частных производных в точке M0 не следует дифференцируемость в точке M0).
В итоге, с учётом теоремы 1.1 формула (1.18) примет вид:
и теорема 1.1. доказана.
Замечание: из дифференцируемости z =f(х,у) в точке M0 следует существование частных производных. Обратное утверждение неверно (из существования частных производных в точке M0 не следует дифференцируемость в точке M0).
В итоге, с учётом теоремы 1.1 формула (1.18) примет вид:
 Следствие. Функция, дифференцируемая в точке M0, непрерывна в этой точке (так как из (1.17) следует, что при Δx
Следствие. Функция, дифференцируемая в точке M0, непрерывна в этой точке (так как из (1.17) следует, что при Δx  где
где
 Используя геометрический смысл (рис.1.3) частных производных
Используя геометрический смысл (рис.1.3) частных производных  и
и  можно получить следующее уравнение (1.24) касательной плоскости πкас s к поверхности: z =f(х,у) в точке C0(x0,y0,z0), z0=z(M):
можно получить следующее уравнение (1.24) касательной плоскости πкас s к поверхности: z =f(х,у) в точке C0(x0,y0,z0), z0=z(M):
 Из сравнения (1.24) и (1.21) получаем геометрический смысл полного дифференциала функции двух переменных:
Из сравнения (1.24) и (1.21) получаем геометрический смысл полного дифференциала функции двух переменных:
 - приращение аппликаты z при движении точки С по касательной плоскости из точки С0 в точку
- приращение аппликаты z при движении точки С по касательной плоскости из точки С0 в точку
 где
где  находится из (1.24).
Уравнение нормали Lн к поверхности: z =f(х,у) в точке С0 получается, как уравнение прямой, проходящей через С0 перпендикулярно к касательной плоскости:
находится из (1.24).
Уравнение нормали Lн к поверхности: z =f(х,у) в точке С0 получается, как уравнение прямой, проходящей через С0 перпендикулярно к касательной плоскости:




