
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Вопрос. Частные производные и дифференциалы высших порядков. Матрица Гессе.
Если функция Мы определили частные производные второго порядка. Третьи частные производные есть производные по соответствующим переменным от вторых производных. Вторые или третьи частные производные часто обозначаются следующим образом: Возникает вопрос о том, влияет ли порядок дифференцирования на вычисленную частную производную. В общем случае влияет, но если функция удовлетворяет некоторым условиям, то нет. Сформулируем соответствующую теорему для случая функции двух переменных. Теорема (Шварца). Если функция
Дифференциалы высших порядков. Пусть в области
где Видим, что Приращения Запишем формулу второго дифференциала для функции двух переменных
Если первый дифференциал символически записать следующим образом
то второй будет иметь вид
Можно показать, что аналогичная формула справедлива для дифференциалов любого порядка:
Формула Тейлора. Теорема. Если функция
Матрица Гессе.
Билет 65. Экстремум функции двух переменных. Функция Необходимое условие экстремума: если дифференцируемая функция Точки, в которых частные производные равны нулю, называются стационарными точками. Стационарные точки и точки, в которых производные не существуют и которые лежат внутри области определения функции, называются критическими точками. Не всякая критическая точка является точкой экстремума. Пусть если если если
|
|||||
|
Последнее изменение этой страницы: 2019-12-15; просмотров: 439; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.137.218.215 (0.007 с.) |
 , определенная в некоторой области
, определенная в некоторой области  , имеет частную производную
, имеет частную производную  по переменной
по переменной  , то эта частная производная вновь является некоторой функцией, которая в свою очередь может иметь частную производную
, то эта частная производная вновь является некоторой функцией, которая в свою очередь может иметь частную производную  . Эта функция называется второй производной функции
. Эта функция называется второй производной функции  по переменным
по переменным  и обозначается символом
и обозначается символом  . Аналогичным образом определяются частные производные
. Аналогичным образом определяются частные производные  .
.
 и так далее.
и так далее. непрерывна вместе со своими вторыми частными производными в некоторой окрестности
непрерывна вместе со своими вторыми частными производными в некоторой окрестности 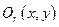 , точки
, точки  , то
, то .
. , имеющая непрерывные частные производные первого порядка. Тогда она будет дифференцируема в этой области, и ее дифференциал имеет вид
, имеющая непрерывные частные производные первого порядка. Тогда она будет дифференцируема в этой области, и ее дифференциал имеет вид ,
, - произвольные приращения независимых переменных
- произвольные приращения независимых переменных  .
. также является функцией от
также является функцией от  , то можно говорить о дифференциале от первого дифференциала
, то можно говорить о дифференциале от первого дифференциала  , который называется дифференциалом второго порядка от
, который называется дифференциалом второго порядка от 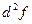 .
. при этом рассматриваются как постоянные и остаются одними и теми же при переходе от одного дифференциала к следующему.
при этом рассматриваются как постоянные и остаются одними и теми же при переходе от одного дифференциала к следующему.

 .
. ,
,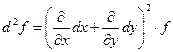 .
.
 определена и непрерывна вместе со своими частными производными до порядка
определена и непрерывна вместе со своими частными производными до порядка  справедлива формула
справедлива формула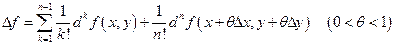 .
.
 имеет максимум (минимум) в точке
имеет максимум (минимум) в точке  , если значение функции в этой точке больше (меньше), чем ее значение в любой другой точке
, если значение функции в этой точке больше (меньше), чем ее значение в любой другой точке  некоторой окрестности точки
некоторой окрестности точки  , то есть
, то есть  (соответственно
(соответственно  ) для всех точек
) для всех точек  ,
,  .
. ,
, 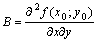 ,
,  и составим дискриминант
и составим дискриминант  . Тогда:
. Тогда: , то функция имеет в точке
, то функция имеет в точке  (или
(или  ) и максимум, при
) и максимум, при  (или
(или  );
);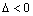 , то в точке экстремума нет;
, то в точке экстремума нет;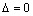 , то требуется дальнейшее исследование (сомнительный случай).
, то требуется дальнейшее исследование (сомнительный случай).


