Программа MORE формирует предположительные значения коэффициентов следующим образом.

Предположим, что неисправность D проявляется в виде симптома S₁ а появление симптома S₁ влечет за собой и появление симптома S₂. В таком случае программа MORE предполагает, что отрицательный коэффициент уверенности, назначенный правилу, которое связывает симптом S₁ с гипотезой D, будет больше или равен отрицательному коэффициенту, назначенному правилу, которое связывает симптом S₂ с гипотезой D. В схеме модели событий на рис. 12.2 ожидается, что С₁= > С₂. Здесь коэффициентом С, оценивается связь между симптомом S₁ и гипотезой D, а коэффициентом С₂ — связь между симптомом S₂ и гипотезой D.

Почему предполагается такое соотношение между значениями коэффициентов, интуитивно понятно. Если отсутствие симптома S₁ является более веским аргументом против гипотезы D, то отсутствие симптома S₂ не меняет положения дел. Если вновь вернуться к модели событий на рис. 12.1, то отрицательная связь между притоком воды и повышением уровня содержания неэмульсионной воды должна быть более "сильной", чем связь между притоком воды и повышением вязкости.

Диагностическая значимость симптома является величиной, обратной количеству гипотез, в которых учитывается наличие этого симптома. В модели событий, схема которой представлена на рис. 12.3, программа MORE предполагает, что С₁ > С₂, поскольку появление симптома S₁ может быть вызвано только неисправностью (гипотезой) D₁, a появление симптома S₂ может быть вызвано и другими неисправностями.

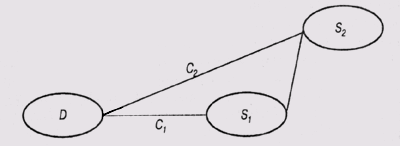
Рис. 12.2. Отрицательные коэффициенты достоверности в цепочке причинно-следственной связи

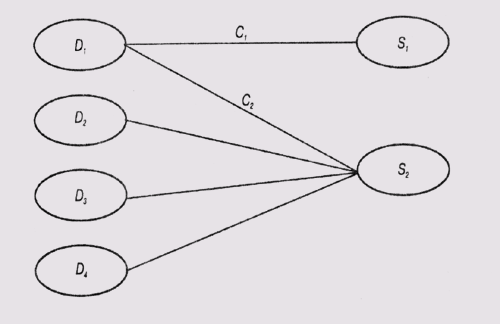
Рис. 12.3. Положительные коэффициенты достоверности в случае множественной связи симптома с гипотезами

Программа MORE также оценивает и отношения между значениями коэффициентов в правилах одного семейства (т.е. в правилах, делающих одинаковое заключение или, что то же самое, относящихся к одной и той же гипотезе). Например, если в семейство правил добавляется новое условие проявления симптома, которое увеличивает условную достоверность симптома, это скажется на тех правилах, которые имеют большие отрицательные значения коэффициентов, чем составные правила. (Напомним, что составными называются правила, расширенные при добавлении нового условия.) Рациональность этих предположений заключается в том, что чем больше мы рассчитываем на появление определенного симптома при данной гипотезе (при данной неисправности), тем сильнее будет наше недоверие к этой гипотезе при отсутствии такого симптома.

Каждое из таких предположений основано на стремлении сохранить взаимную согласованность коэффициентов в правилах одного семейства.

Опыт эксплуатации системы MORE

В одной из своих ранних работ, посвященных созданию системы MYCIN, Шортлифф обратил внимание на необходимость разработки такого механизма извлечения знаний, который помогал бы эксперту назначать порождающим правилам коэффициенты уверенности [Shortliffe, 1976]. В сборнике [Buchanan and Shortliffe, 1984, Chapter 10, Section 5] собрано множество статей, в которых обсуждается ряд вопросов, связанных с этой проблемой. В этих статьях, в частности, обсуждается, как добавлять новые правила в существующий набор и как модифицировать ранее сформулированные правила.

Тот подход, который использован в программе MORE, достаточно прозрачен и понятен. Но в этой программе совершенно не затрагивается вопрос о независимости значений коэффициентов, который был в свое время поднят Шортлиффом. В главе 6 мы видели, что применение теоремы Байеса требует, чтобы свидетельства в пользу гипотез были независимыми, если мы собираемся комбинировать их параметры с помощью простой мультипликативной схемы.

Шортлифф предложил сгруппировать зависимые свидетельства в одном правиле, а не распределять их по множеству и рассматривать такую группу свидетельств в качестве "суперсимптома". Оценку весомости этого суперсимптома можно сделать на основе аппроксимации конъюнкции весов индивидуальных свидетельств. В программе MORE это предложение не реализовано, но в ней имеется вся необходимая для этого информация, представленная в модели событий. Анализ функционирования системы подтвердил предположение, что при нарушении независимости свидетельств коэффициенты уверенности отклоняются в значительно большем диапазоне, чем вероятности (см. об этом в [Buchanan and Shortliffe, 1984, Chapter 11, Section 5]).

Кан обратил внимание на другие проблемы, обнаруженные при эксплуатации прототипа системы MORE.