Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Решение обыкновенных дифференциальныхСодержание книги Похожие статьи вашей тематики
Поиск на нашем сайте
Соломатин А.С. С60 Моделирование гидравлических и теплообменных процессов с применением пакета MATLAB: учеб. пособие / А. С. Соломатин, В. Н. Калинкин, Т. Н. Гартман, Д. К. Новикова; под ред. проф. Т.Н. Гартмана. - М.: РХТУ им. Д. И. Менделеева, 2011. – 129 с.:ил. ISBN
Представлены примеры решения некоторых типовых задач моделирования процессов в гидравлических и теплообменных системах с применением математического пакета MATLAB. Для удобства пользования учебным пособием приводится краткое описание пакета MATLAB. Результаты расчетов представлены в табличном и графическом виде. Материал изложен в доступной форме и содержит наглядные иллюстрации и тексты программ. Предназначено для студентов химико-технологических специальностей вузов. УДК 66.011.001:662.95 ББК © Российский Химико-Технологический Университет им. Д. И. Менделеева, 2011
ОГЛАВЛЕНИЕ Предисловие…………………………………………………….4 Глава 1. Краткие основы работы в MATLAB…………….5 1.1. Интерфейс. …………………………………………………………5 1.2. Редактирование М-файлов …………………………………...8 1.3. Построение графиков……………………………………………12 1.4. Построение поверхности………………………………………13 1.5. Операции с матрицами. ……………………………………….14 1.6. Нелинейные уравнения и системы…………………………...15 1.7. Интегрирование……………………………………………………16 Решение обыкновенных дифференциальных уравнений и систем………………………………………18 1.9. Поиск экстремума функции одной переменной…………...21 1.10. Поиск экстремума функции нескольких переменной…..21 ГЛАВА 2. Моделирование простых гидравлических систем…………………………...23 2.1. Стационарный режим движения жидкости ……………….23 2.2. Нестационарный режим движения жидкости …………….47 ГЛАВА 3. Моделирование стационарных режимов Процессов теплопередачи в теплообменниках различных типов………………………………………….68 3.1. Теплообменник типа смешение–смешение…………………70 3.2. Теплообменник типа смешение–вытеснение ……………..82 Прямоточный теплообменник типа труба в трубе (решение задачи Коши)………………99 Противоточный теплообменник типа труба в трубе (решение краевой задачи) ………….112 Предисловие Методы математического моделирования широко применяются в настоящее время при проектировании и управлении химико-технологическими процессами. Важнейшим аспектом стратегии математического моделирования является компьютерная реализация разработанных моделей протекающих в аппаратах процессов, которая тесно связана с применением различных математических пакетов программ, таких, например, как MATLAB. Основная задача настоящего учебного пособия на простых примерах научить студентов применять пакет MATLAB для построения расчетных модулей химико-технологических процессов. С этой целью решаются задачи моделирования гидравлических процессов и процессов теплопередачи в простейших типовых аппаратах химической технологии. При этом подробно представлены последовательные этапы компьютерного моделирования: постановка задачи, анализ систем уравнений математического описания, разработка и выбор алгоритмов решения, составление программ расчета и программная реализация вычислительных алгоритмов, табличная и графическая интерпретация промежуточных и конечных результатов вычислений. анализ параметрической чувствительности моделей, а также их статических и динамических характеристик. Для контингента студентов, имеющих недостаточный опыт работы с пакетом MATLAB, в отдельной главе изложены его основные функциональные возможности. Приведенные в пособии коды программных модулей включают многочисленные комментарии и могут использоваться при решении практических задач оптимизации химико-технологических процессов. Авторы настоящего учебного пособия с благодарностью отнесутся к замечаниям и предложениям по улучшению его смыслового содержания. Глава 1. Краткие основы работы в MATLAB Интерфейс.
Рис. 1.1. Интерфейс. Основное окно.
В рабочей области находится знак >> после которого расположен курсор. Эту строку называют командной строкой. В нее с клавиатуры вводятся команды. Нажатие Enter заставит выполнить команду и вывести результат в том же окне. (см. рис. 1.1.) Так как текст в окне по мере работы смещается (уступает место новым командам и выводимым данным) то для просмотра выехавшей за окно части текста используют полосы прокрутки или клавиши Page Up, Page Down. Клавиши ↑ и ↓ позволяют вернуть в командную строку ранее введенные команды или другую входную информацию (она вся обязательно автоматически хранится и всегда доступна). Кнопка ↑ помещает в командную строку предыдущую команду, а если еще раз ее нажать то еще предыдущую и так далее. Кнопка ↓ выводит команды (ранее набранные) в обратном порядке. Видимая часть информации (то есть то что поместилось в окне) называется зоной просмотра, а командная строка зоной редактирования. В зоне просмотра ничего нельзя исправить или ввести. Можно только выделить мышкой для копирования. Если команда заканчивается; то результат ее выполнения не отображается в командной строке. Иначе, то есть если строка не заканчивается на; то результат сразу же после нажатия на Enter выводится в окне ниже этой команды. (см. рис. 1.1) Значения всех переменных, вычисленные в течение работы, сохраняются в специальной области памяти, называемой Workspace. (см. на рис. 1.1) Определения всех переменных и функций и их последние перед закрытием программы значения можно сохранить на диск в файл с расширением.mat но само содержание Command Window при выключении МАТЛАБа не сохраняется никаким способом. Примеры выполнения арифметических операций показаны на рис.1.1. Для строк символов необходимо текст помещать в ‘одинарные кавычки’. Для сложения строк символов используется операция strcat, как показано на рис.1.1. В главном меню (см. рис.1.1) следует обратить внимание на команду Desktop (настройка среды МАТЛАБ). При нажатии раскроется список, содержащий Desktop Layout который предлагает на выбор: · Default устанавливает настройку принятую по умолчанию, то есть открывает окна Command Window, Workspace, Command History, Current Directory. · Command Window Only открывает только окно Command Window. · History and Command Window открывает соответствующие окна. · All Tabbet показывает окно справки, окно управления М-файлами и внизу ярлычки рабочих окон, которые можно выбрать щелчком. Также работа может осуществляться в программном режиме, то есть в командной строке указывается имя М-файла (файл с расширением.m), который содержит программу действий (алгоритм) и может рассматриваться как функция, то есть при указании его имени (без указания расширения) в командной строке выполняются запрограммированные в нем операции. (см.рис.1.2). Как выгладит содержимое М-файла, см. рис.1.3. Числовые переменные могут быть с плавающей точкой (тогда указывается порядок, например 6.4713e+003) или с фиксированной точкой (например 81.5000). Текстовые комментарии начинаются со знака % (см.рис.1.2). Все функции разделяются на встроенные и определенные пользователем. Встроенные, например, это y=sin(x); y=atan(x); y=exp(x); y=log(x) натуральный логарифм, а вот y=log10(x) десятичный логарифм, y=fix(x) округление до ближайшего целого в сторону нуля, y=floor(x) округление до ближайшего целого в сторону отрицательной бесконечности, y=ceil(x) округление до ближайшего целого в сторону положительной бесконечности, y=round(x) обычное округление Массив задается так: ИМЯ_МАССИВА = НАИМЕНЬШ_ЭЛ-Т_МАСС: ШАГ_ИЗМЕН_ЭЛ-ТА_МАСС: НАИБОЛЬШ_ЭЛ-Т_МАСС; (см. рис.1.2). Обращение к элементу массива y=x_mas(2); где в скобках указывается порядковый номер (индекс) элемента массива (см. рис.1.2). Редактирование М-файлов «File»—«New»--«M-file» позволяет открыть окно Editor то есть Редактор М-файлов. В этом окне напечатать текст программы, которая должна быть выполнена, когда имя этого М-файла будет указано в командной строке в Command Window. Иначе можно запустить командой “Debug”—“Run” в меню редактора.
Рис. 1.4. Сохранение М-файла (то есть описанная в нем программа считается функцией и ее описание начинается с указания какого-нибудь имени этой функции, под которым она дальше и будет вызваться для исполнения). (см.рис.1.4.) Если какие-то М-файлы уже созданы ранее то их можно посмотреть командой File—Open и выбрать тот который нужен. При написании программы можно писать комментарии начиная их со знака %. (см.рис.1.3). Function y=f(x) %функция вычисляется от одного аргумента и возвращает одно %значение, или от вектора аргумента и возвращает вектор, каждый %элемент которого вычислен от соответствующего элемента вектора %аргумента y=(x+2).*(x-4); %поэтому перед знаком *умножения стоит.точка.* %если не ставить;точку с запятой в конце строки то произойдет вывод на %экран end символьная переменная в М-файле: str=’P I Pupkin’ ее символьное содержимое заключается в кавычки. Ввод: xleft=input('введите левую границу интервала поиска '); Вывод: disp('ВВОД ИСХОДНЫХ ДАННЫХ края диапазона поиска, точность по аргументу ИЛИ по функции '); disp(string); Построение графиков % подготовка к построению графика h=0.1; x1=xleft:h:xright; % создан массив точек для графика y1=f(x1); % создан массив точек для графика plot(x1,y1,’k-‘); grid on; % покрыт сеткой title('y=(x+2)(x-4)'); % подпись наверху xlabel('X'); % подпись к оси ylabel('Y'); text(x,y,’\leftarrow Minimum’);%подпись Minimum к стрелке влево, %которая будет указывать на точку с координатами x,y. zeroMas=x1*0; hold on; %обеспечивает построение нового графика в том же окне plot(masx,masy,’r.’); % график построен legend(‘plot with minimal step’,’plot with your step’,0); hold on; plot(x1,zeroMas,’k-‘,zeroMas,y1,’k-‘); % построены оси результат этих действий смотри ниже на рис.1.5. В результате обращения к функции plot(x,y) будет создано окно с именем Figure 1 (так обычно по умолчанию) в котором будет построен график функции У от Х если заранее заданы массив Х и соответствующий ему массив значений функции У. Тип линии указывается в кавычках plot(x1,y1,'k-'); ‘k-‘ Черная сплошная линия. ‘r.’ Круглые красные маркеры без линии. hold on блокирует создание нового окна то есть новый график будет построен поверх старого на тех же координатных осях.
Рис. 1.5. Пример построения графика Построение поверхности Обеспечивается следующим текстом программы (см. рис. 1.6) % подготовка к построению графика masx=xleft:hx:xright; masy=yleft:hy:yright; masz=fz_xy2(masx,masy); построены массивы координат для точек %графика mesh(masx,masy,masz); %построена сеточная поверхность grid on; title(‘z=-sqrt(256-x.^2-y.^2)’); xlabel(‘X’); ylabel(‘Y’); zlabel(‘Z’); text(x,y,z,’\leftarrow Minimum’); legend(‘z(i,j)=-sqrt(256-x(i)*x(i)-y(j)*y(j))’,0); где команда mesh(masx,masy,masz); строит сеточную поверхность.
Рис. 1.6. Пример построения поверхности
Операции с матрицами. Пусть даны две матрицы. (Если не даны, зададим их. Пусть A=[1 2 3; 5 67 89; 34 21 5]; B=[3 4 5; 54 32 12; 6 7 8]; Тогда имеем две матрицы 3х3 элемента). Транспонировать матрицу можно так A_transp=A’; где знак ’ обеспечивает транспонирование матрицы А. Умножение матриц выполняется так C_res_mult=A*B; где C_res_mult результат умножения матриц. Обратная матрица находится так А_obr=A^(-1); Или так: A_obr=inv(A); Поэлементное сложение матриц C=A+B; Определитель D=det(A); Решение системы линейных уравнений, где А матрица системы, столбец b столбец свободных членов, столбец х столбец неизвестных: x=linsolve(A,b); Интегрирование Для решения определенного интеграла методом трапеций предусмотрена функция trapz. Пример для вышеописанной функции func (см. рис.1.8), (где для обработки вектора аргументов поставлена точка перед знаком возведения в степень y=0.2*exp(x) -2*(x-1).^2;) при пределах интегрирования [0 1] с шагом разбиения 0,1 приведен на рис.1.9. Вполне очевидно, что с ростом числа точек разбиения по х (числа шагов, то есть при уменьшении шага по х) будет расти точность вычисления интеграла. На рис.1.9 наглядно показано разбиение интервала интегрирования по х с заданным шагом, а также вектор значений функции в точках разбиения по х (то есть при данных значениях аргумента).
Рис. 1.9. Интегрирование
Рис. 1.11. функция ode113 строит график решения
Используем функцию ode23 решающую методом Рунге-Кутта 2-3 порядка. Ее вызов [T, Y]=ode23(@syst, [0 10], [0 0]); Рис. 1.12. функция syst(t,y) где явно указаны выходные параметры вектор Т и матрица Y, а также указаны интервал [0 10] и начальные значения [0 0].
Рис. 1.13. график решения
Рис. 2.1. Простая гидравлическая система Для системы, изображенной на рис. 2.1, будут справедливы два уравнения массового баланса (третье возможное балансовое уравнение – уравнение общего баланса – получается сложением двух других, т. е. будет линейно-зависимым):
Формула для определения скорости
где k – коэффициент пропускной способности клапана, Р вх, Р вых – давления жидкости на входе и на выходе из клапана. Более строгая запись формулы (3) имеет вид:
где sgn(x) – функция знака и может принимать только три значения: –1, 0, +1 в соответствии со схемой: sgn(x) = – 1, если х < 0; sgn(x) = 0, если х = 0; (5) sgn(x) = +1, если х > 0. При этом знак скорости потока жидкости становится отрицательным, если направление ее движения будет противоположным направлению, указанному на рис. 2.1. Так как гидравлическая система содержит 5 клапанов, то приведенных формул (3) в системе уравнений математического описания должно быть 5. По аналогии, должно быть две группы уравнений, определяющих давление жидкости внизу закрытой емкости и давление газа над поверхностью жидкости. При этом принимаются допущения: · об идеальном поведении газа в емкости; · о цилиндрической форме закрытой емкости с площадью поперечного сечения S и геометрической высотой НG; · об одинаковом давлении газа РN в емкостях, не заполненных жидкостью. В соответствии со следствием из закона Паскаля давление жидкости Р жидк внизу емкости определяется по формуле: Р жидк. = P газ + r gH, (6) где Р газ – давление газа над поверхностью жидкости; r – плотность жидкости; Н – уровень жидкости в емкости. Для определения давления газа Р газ используется соотношение для идеального газа: где В результате будет справедливо: Р газ S (HG – H) = PN S HG или
Формулы для определения давления жидкости Р жидк (6) и давления газа Р газ (8) используются для описания поведения двух закрытых емкостей в гидравлической системе, изображенной на рис. 2.1. Программа расчета процесса Программа расчета процесса Рис. 3.2. Трубчатый теплообменник
В настоящем разделе приведены алгоритмы поверочно-оценочного расчётов стационарных режимов типовых фрагментов поверхностных теплообменников, в которых учитываются только процессы теплопередачи. Рис. 3.4. Схематическое изображение теплообменника типа смешение–смешение Представленная на рис. 3.4 схема теплообменника включает в себя два потока теплоносителей – например, охлаждаемый поток c начальной температурой (на входе в аппарат) Для упрощения построения математического описания рассматриваемого процесса принимаются следующие допущения: · стационарный режим теплопередачи; · модель идеального смешения для обоих потоков теплоносителей; · происходит только процесс теплопередачи. Программа расчета процесса Рис. 3.7. Схематическое изображение теплообменника смешение–вытеснение Представленная схема змеевикового теплообменника включает в себя два потока теплоносителей – поток в резервуаре c начальной температурой (на входе в аппарат) Для построения математического описания данной модели примем следующие допущения: · поток, проходящий через резервуар, описывается гидродинамической моделью идеального смешения; · поток в змеевике описывается гидродинамической моделью идеального вытеснения; · рассматривается стационарный режим работы теплообменника; · коэффициент теплопередачи считается постоянным; · кроме теплопередачи никаких процессов не происходит; · теплоёмкости теплоносителей одинаковы и не меняются с изменением температуры. Рис. 3.9. Зависимость температуры теплоносителя в змеевике от длины змеевика Уравнение 2 системы (41) для решения на компьютере представляется в конечно-разностной форме согласно нумерации системы (41 – это будет уравнение
где Уравнение 1 (корректирующее уравнение) – это внешний цикл решения задачи; уравнение 2 – цикл решения дифференциального уравнения, внутренний цикл решения задачи. Корректирующее уравнение 1 представляется в следующем виде:
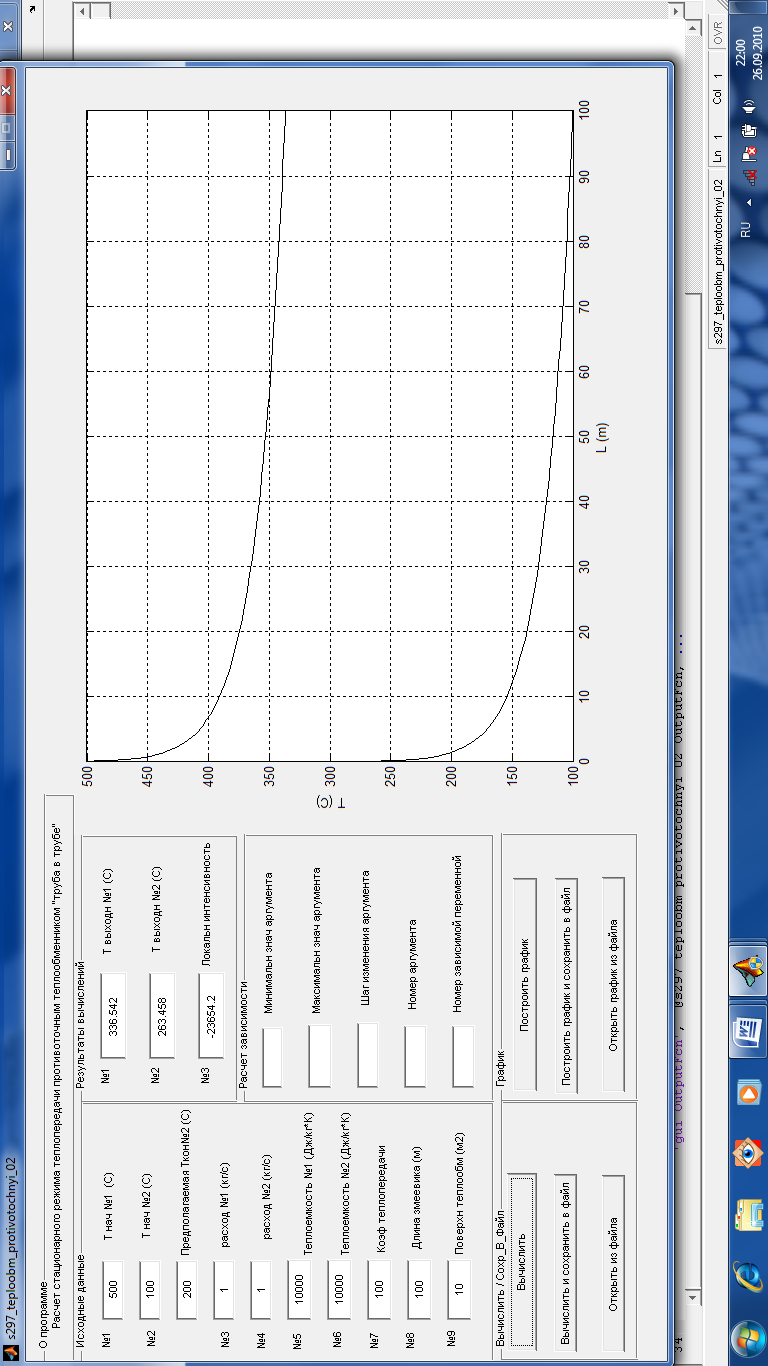
где Во внешнем цикле решения может быть применен, например, метод половинного деления для решения одного уравнения (44). Во внутреннем цикле решается дифференциальное уравнение (37) или соответственно (43) (например, методом Эйлера) при каждом очередном приближении Т 1. Рис. 3.10. Блок-схема алгоритма поверочно-оценочного расчёта стационарного режима процесса в теплообменнике типа смешение–вытеснение Программа расчета процесса Рис. 3.11. Ввод исходных данных и получение расчетных результатов, в том числе графика зависимости температуры в змеевике от продольной координаты
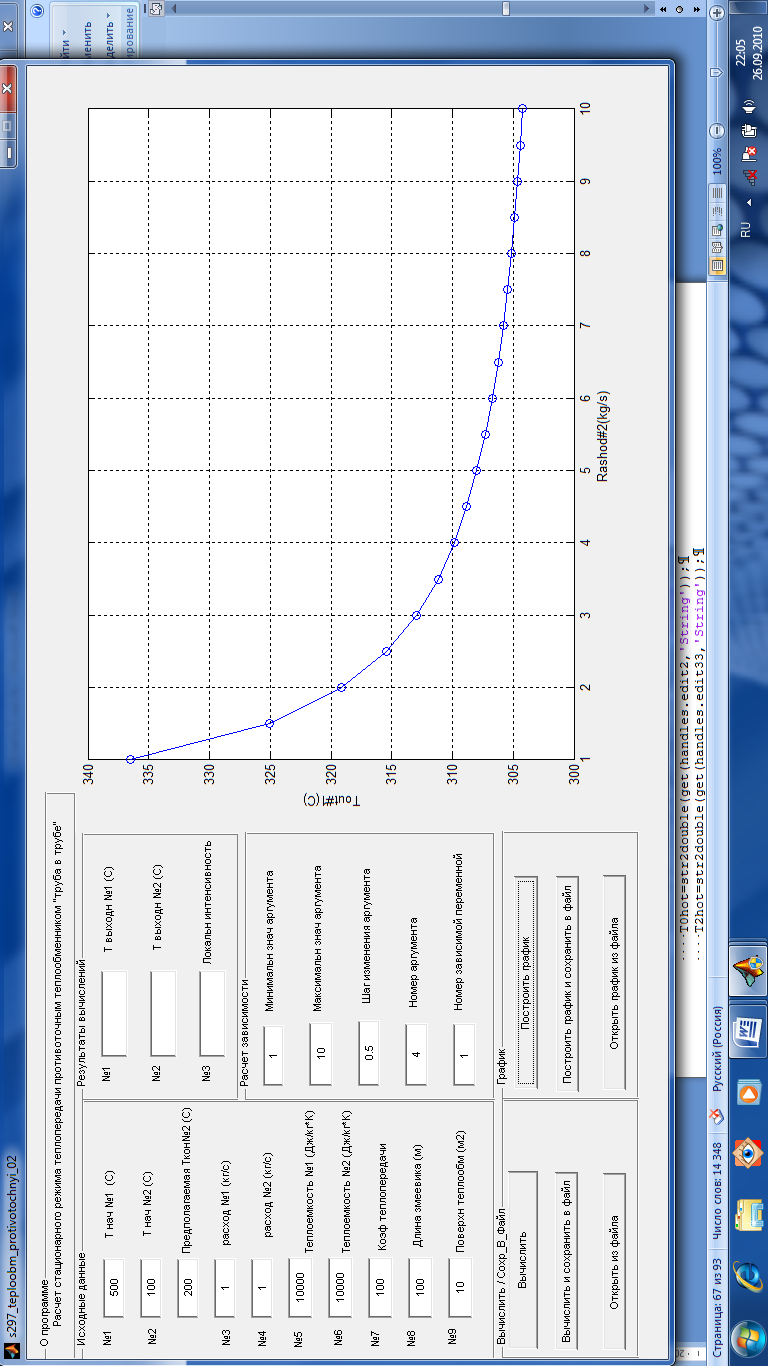
Рис. 3.12. Построение графика: зависимость температуры потока №1 на выходе из теплообменника от расхода
Рис. 3.13. Схематическое изображение прямоточного теплообменника типа труба в трубе
Представленная схема теплообменника включает в себя два потока теплоносителей – например, охлаждаемый поток c начальной температурой (на входе в аппарат) Для построения системы уравнений математического описания процесса в прямоточном теплообменнике типа труба в трубе принимаются следующие допущения: · рассматривается стационарный режим процесса теплопередачи; · не происходит никаких других процессов, только процесс теплопередачи; · коэффициент теплопередачи постоянен и известен; · теплоёмкость потоков теплоносителей постоянна; · поверхность теплообмена равномерно распределена вдоль участка длины теплообменника; · движение первого и второго потоков теплоносителей описывается гидродинамической моделью идеального вытеснения. Рис. 3.14. Изменение температур теплоносителей по длине теплообменника типа труба в трубе (прямоток)
Программа расчета процесса Рис. 3.18. Схематическое изображение противоточного теплообменника типа труба в трубе Представленная схема противоточного теплообменника включает в себя два потока теплоносителей – например, охлаждаемый поток c начальной температурой (на входе в аппарат) Основные допущения для построения этой модели нужно принять такими же, как в случае прямоточного теплообменника «труба в трубе».
Программа расчета процесса Рис. 3.20. Блок-схема алгоритма поверочно-оценочного расчёта стационарного режима в противоточном теплообменнике типа труба в трубе
Москва
Учебное издание
СОЛОМАТИН Алексей Сергеевич Соломатин А.С. С60 Моделирование гидравлических и теплообменных процессов с применением пакета MATLAB: учеб. пособие / А. С. Соломатин, В. Н. Калинкин, Т. Н. Гартман, Д. К. Новикова; под ред. проф. Т.Н. Гартмана. - М.: РХТУ им. Д. И. Менделеева, 2011. – 129 с.:ил. ISBN
Представлены примеры решения некоторых типовых задач моделирования процессов в гидравлических и теплообменных системах с применением математического пакета MATLAB. Для удобства пользования учебным пособием приводится краткое описание пакета MATLAB. Результаты расчетов представлены в табличном и графическом виде. Материал изложен в доступной форме и содержит наглядные иллюстрации и тексты программ. Предназначено для студентов химико-технологических специальностей вузов. УДК 66.011.001:662.95 ББК © Российский Химико-Технологический Университет им. Д. И. Менделеева, 2011
ОГЛАВЛЕНИЕ Предисловие…………………………………………………….4 Глава 1. Краткие основы работы в MATLAB…………….5 1.1. Интерфейс. …………………………………………………………5 1.2. Редактирование М-файлов …………………………………...8 1.3. Построение графиков……………………………………………12 1.4. Построение поверхности………………………………………13 1.5. Операции с матрицами. ……………………………………….14 1.6. Нелинейные уравнения и системы…………………………...15 1.7. Интегрирование……………………………………………………16 Решение обыкновенных дифференциальных уравнений и систем………………………………………18 1.9. Поиск экстремума функции одной переменной…………...21 1.10. Поиск экстремума функции нескольких переменной…..21
|
||||
|
Последнее изменение этой страницы: 2017-02-19; просмотров: 574; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.15.26.184 (0.013 с.) |








 Напишем М-функцию syst (см. рис.1.12)
Напишем М-функцию syst (см. рис.1.12)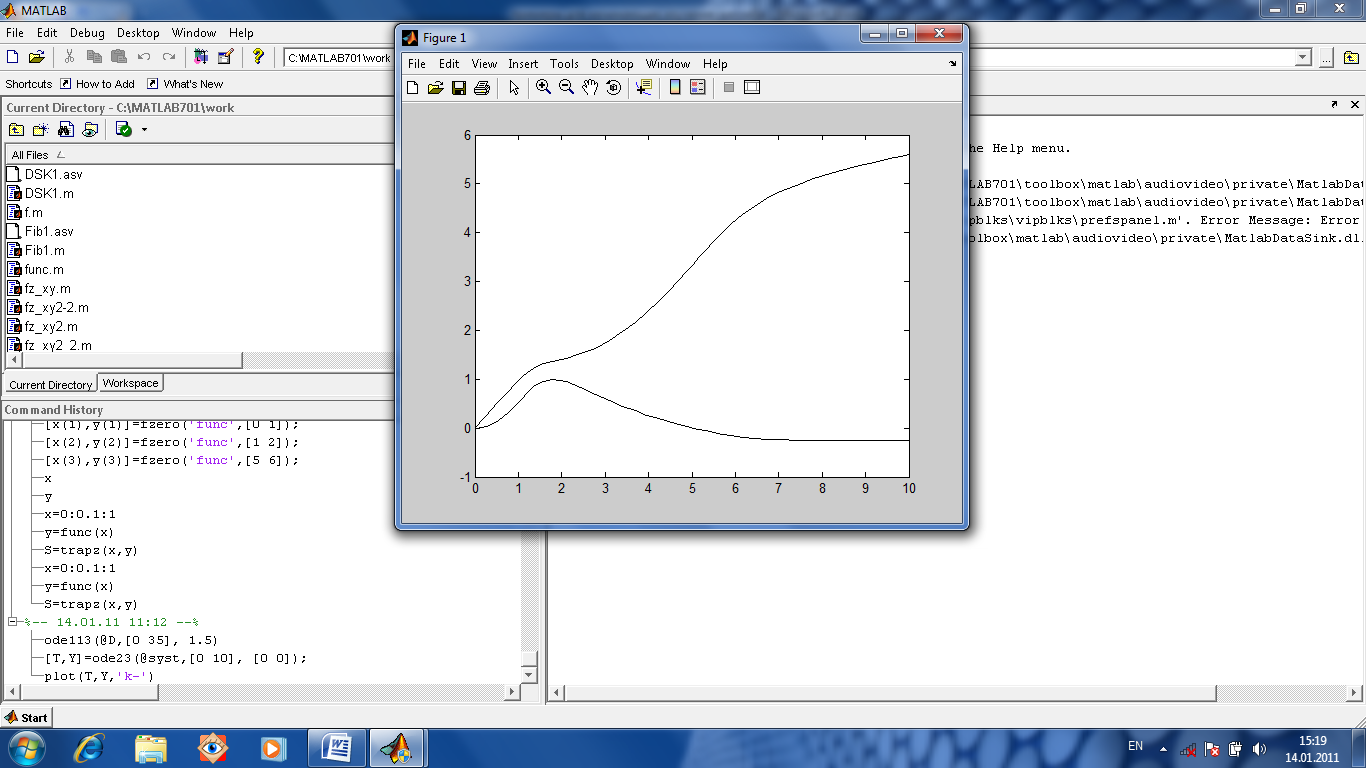 Затем формируем график решения plot(T,Y,’k-‘). Получаем график (см.рис.1.13)
Затем формируем график решения plot(T,Y,’k-‘). Получаем график (см.рис.1.13)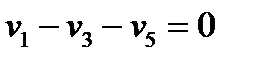 ; (1)
; (1)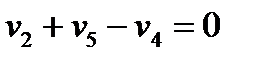 . (2)
. (2)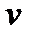 протекания жидкости через клапан в соответствии с уравнением Бернулли для суммарной удельной энергии элементарной струи идеальной жидкости при установившемся движении и с учетом допущений о простой гидравлической системе имеет вид:
протекания жидкости через клапан в соответствии с уравнением Бернулли для суммарной удельной энергии элементарной струи идеальной жидкости при установившемся движении и с учетом допущений о простой гидравлической системе имеет вид: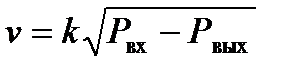 , (3)
, (3)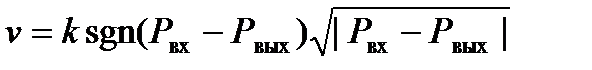 , (4)
, (4)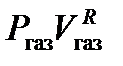 =
= 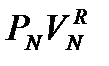 =const, (7)
=const, (7)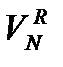 – объем пустой емкости, т. е. не заполненной жидкостью,
– объем пустой емкости, т. е. не заполненной жидкостью, 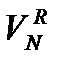 = S × HG;
= S × HG; 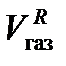 – объем газа в закрытой емкости,
– объем газа в закрытой емкости, 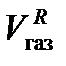 = S (HG – H).
= S (HG – H).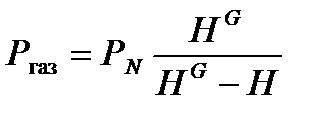 . (8)
. (8) Рис. 3.3. Змеевиковый теплообменник
Рис. 3.3. Змеевиковый теплообменник , конечной температурой (на выходе)
, конечной температурой (на выходе)  , расходом
, расходом  , теплоёмкостью
, теплоёмкостью  и нагреваемый поток c начальной температурой (на входе в аппарат)
и нагреваемый поток c начальной температурой (на входе в аппарат)  , конечной температурой (на выходе)
, конечной температурой (на выходе) 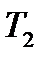 , расходом
, расходом 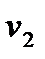 , теплоёмкостью
, теплоёмкостью  . Поверхность теплообмена имеет площадь
. Поверхность теплообмена имеет площадь 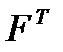 . Коэффициент теплопередачи обозначен
. Коэффициент теплопередачи обозначен  .
. , расходом
, расходом  :
:
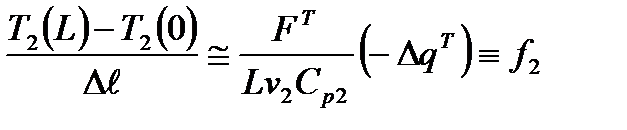 , (43)
, (43) – правая часть дифференциального уравнения (37) и конечно-разностного уравнения (43), расчет которой необходим для определения дискретных значений функции
– правая часть дифференциального уравнения (37) и конечно-разностного уравнения (43), расчет которой необходим для определения дискретных значений функции 
 .
.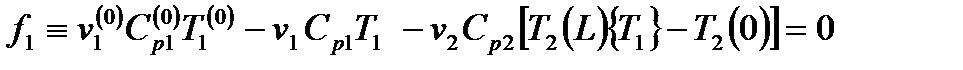 , (44)
, (44) – функция этого уравнения, решаемого относительно
– функция этого уравнения, решаемого относительно  .
.


 , расходом
, расходом 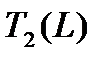 , расходом
, расходом  , конечной температурой (на выходе)
, конечной температурой (на выходе)  , конечной температурой (на входе)
, конечной температурой (на входе)  , расходом
, расходом