Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Фундаментальное уравнение адсорбции ГиббсаСодержание книги Похожие статьи вашей тематики
Поиск на нашем сайте
Адсорбции в координатах «A-p/Pf (а) и линейной формы уравнения (4.21)(б) теризует отношение интегральной теплоты (а не ее изменение) к изменению адсорбции от Л, до А2. В начале процесса при формировании первого адсорбционного слоя дифференциальная теплота адсорбции достигает максимального значения. С ростом А интегральная теплота адсорбции увеличивается, а дифференциальная теплота адсорбции может уменьшаться, увеличиваться или оставаться неизменной в зависимости от природы адсорбата и адсорбента. Упражнения 1. Какую часть от абсолютной адсорбции составляет избыточная адсорбция, если в результате адсорбции концентрация адсорбата увеличилась в 17раз? Согласно условию задачи концентрация адсорбата в адсорбционном слое св = 17с. На основании равенств (4.1) и (4.2) можно определить избыточную адсорбцию: Г = А-сп = cBh - ch = (св - c)h. Отношение избыточной и абсолютной адсорбции 1А c*h 17c 17 Избыточная адсорбция составляет 0,941 часть, или 94,1% от абсолютной адсорбции. 2. Как соотносится адсорбция, выраженная в моль/м2г и моль/кг,на порошке с диаметром частиц 70 мкм и плотностью 1,25-Ю3 м3/кг? Воспользуемся формулами (1.1), (1.4) и (4.4): = Г"—-
В MBva
ар 70-10 6 1,25-103 3. Твердое тело поместили в газовую среду. Химическиий потенциал вещества в
4. Энергия связи между адсорбатом и адсорбентом составляет 215 кДж/ Высокое значение энергии связи свидетельствует о том, что протекает хе-мосорбция. Г л а в a 5
На границе раздела жидкость — газ (вода — воздух) могут самопроизвольно адсорбироваться молекулы поверхностно-активных веществ (ПАВ). Они формируют пограничные адсорбционные слои, которые способны радикально изменять свойства поверхности раздела фаз и дисперсных систем. Систематическое изучение свойств растворов и адсорбции ПАВ было начато еще в 20-х годах П.А.Ребиндером. В настоящее время эти исследования продолжаются и углубляются, в том числе последователями и учениками П.А.Ребиндера.
С с а б Рис. 5.1. Изотермы поверхностного натяжения (а) и адсорбции (б): / — для поверхностно-активных веществ; 2 — для поверхностно-инактивных веществ; 3 — касательная для определения поверхностной активнности; ст() — поверхностное натяжение чистого растворителя (5-1) где g — поверхностная активность вещества. Размерность поверхностной активности определяется размерностью поверхностного натяжения (Дж/м2 или Н/м) и концентрации (моль/м3), т.е. она может выражаться в Джм/моль или Нм2/моль. Значение поверхностной активности графически может быть определено как тангенс угла наклона касательной (прямая 5на рис 5.1, а) к изотерме поверхностного натяжения (кривая 1) в точке, которая соответствует поверхностному натяжению чистого растворителя, т.е. g = tga. Знак поверхностной активности и характеризует адсорбцию различных веществ. В случае адсорбции ПАВ поверхностная активность g > 0, и согласно условию (5.1) производная da/dc < 0. На основании уравнения (4.18) гиббсовская адсорбция для ПАВ равна Г>0, а изотерма адсорбции (см. рис. 5.1, б) графически аппроксимируется кривой 7. Адсорбция ПАВ на границе раздела раствор вещества — газ (водный раствор вещества — воздух) заключается в самопроизвольном переходе значительной части растворенного вещества на межфазовую поверхность, то есть протекает процесс, в котором интенсивная величина — концентрация — не выравнивается, а становится различной. В результате адсорбции концентрация вещества в адсорбционном слое св поверхности жидкости превышает его концентрацию в объеме с. В случае адсорбции поверхностно-инактивных веществ производная da/dc > 0, и с увеличением концентрации этих веществ поверхностное натяжение возрастает (см. рис. 5.1, я, кривая 2). В соответствии с уравнением (4.18) Г<0, отрицательное значение гиббсовской адсорбции для поверхностно-инактивных веществ означает, что растворенного вещества в объеме находится больше, чем в адсорбционном поверхностном слое. Этот процесс можно рассматривать как десорбцию вещества из поверхностного слоя в объем. Изотерма адсорбции в этом случае проходит ниже оси абсцисс (см. рис. 5.1, б, кривая 2). К поверхностно-инактивным веществам относятся некоторые водные растворы электролитов (кислот, щелочей и солей), которые способны диссоциировать на ионы и молекулы которых по сравнению с молекулами воды более полярны. Увеличение поверхностного натяжения и соответственно снижение адсорбции растворов поверхностно-инактивных веществ происходит менее резко, чем изменение этих же параметров для растворов ПАВ (сравним кривые / и 2 на рис. 5.1). При отрицательной адсорбции концентрация веществ в поверхностном слое будет меньше, чем в объеме, поэтому поверхностное натяжение разбавленных растворов инактивных веществ незначительно отличается от поверхностного натяжения чистого растворителя.
Адсорбция ПАВ Молекулы ПАВ имеют асимметричное, или дифильное, строение. Рассмотрим строение молекулы ПАВ на примере валериа- новой кислоты (рис 5.2, а). Длинная часть молекулы 2 представляет собой углеводородный радикал. Этот радикал неполярен и гидрофобен, он не обладает сродством к воде. Другая часть молекулы ПАВ, обычно меньшая, содержит гидрофильную полярную группу 7, которая обладает сродством к воде. В случае валериановой кислоты это карбоксильная группа —СООН. Схематически молекулу ПАВ изображают в виде кружка (гидрофильная полярная группа) и черточки (гидрофобная нсполярная группа). Кроме карбоксильной группы гидрофильную часть молекул ПАВ могут составлять другие группы, обладающие значительным дипольным моментом и сродством к воде. К числу таких групп относятся — ОН, -СНО, -NH2, -SH, -CNS, -SO2H, -CN, -NO и др. Натриевая соль стеариновой кислоты, которая входит в состав мыла, также является ПАВ. Но в отличие от валериановой кислоты, которая практически не диссоциирует в воде и не образует ионы, стеарат натрия диссоциирует в водном растворе, образуя поверхностно-активный анион: образуется монослой, т.е. один ряд адсорбированных молекул (см. рис. 5.2, б). Особенности адсорбции ПАВ, в том числе стеарата натрия, рассмотрены в гл. 20. В результате адсорбции ПАВ снижается поверхностное натяжение. Так, поверхностное натяжение воды при температуре 293 К составляет 72,75 мДж/м2, а для 0,24%-го раствора валериановой кислоты оно составляет 42,1 мДж/м2; поверхностное натяжение 510~3 моль/л водного раствора стеарата натрия равно примерно 30 мДж/м2. Поверхностное натяжение сырого молока колеблется в пределах 45—60 мДж/м2, т.е. оно ниже, чем у воды. Причиной снижения поверхностного натяжения являются фосфолипиды — ПАВ, содержащие несколько функциональных гидрофильных групп. В состав молока входят также жирные карбоновые кислоты и другие вещества, обладающие поверхностно-активными свойствами. Эфиры сахарозы, которые образуются в процессе производства сахара, применяют в различных отраслях пищевой промышленности; 0,1%-й раствор эфиров сахарозы снижает поверхностное натяжение воды до 30 мДж/м2. ПАВ в состоянии изменять не только поверхностные, но и объемные свойства жидкости (см. гл. 21).
C17H35COONa С17Н35СОО Na+,
анион С17Н35СОО~ имеет длинный углеводородный радикал. Если гидрофобная часть молекулы ПАВ длинная, то ее изображают ломаной линией, как это показано в нижней части рис. 5.2, а. Более подробно строение и свойства ПАВ рассмотрены в гл. 21. Вследствие дифильного строения молекулы ПАВ адсорбируются на границе раздела фаз вода — воздух, ориентируясь при этом определенным образом. Гидрофильная часть молекул, обладающая сродством к полярным молекулам воды, взаимодействует с водой, а неполярная гидрофобная часть выталкивается в неполярную фазу (воздух).
При определенной концентрации раствора валериановой кислоты достигается предельная адсорбция и на поверхности воды
Рис. 5.2. Строение молекулы валериановой кислоты (а) и адсорбционный слой ПАВ на границе раздела жидкость-газ (б) Адсорбтива
Да = а0 - а = - Л77Чп(1 - Г/TJ. (5.8) Если уравнение Шишковского (5.2) связывает поверхностное натяжение с концентрацией адсорбтива, а уравнение Ленгмюра (4.34) — адсорбцию с концентрацией, то уравнение Фрумкина определяет изменение поверхностного натяжения в зависимости от адсорбции. Фундаментальное уравнение Гиббса (4.18) связывает все параметры, которые характеризуют адсорбцию (а, с, Г) Предельная адсорбция Величину Г^ которая согласно условию (4.3) равна А^ входящую в уравнение Ленгмюра (4.34), называют предельной адсорбцией. Увеличение концентрации ПАВ приводит к росту адсорбции, но после достижения определенной концентрации ПАВ адсорбция перестанет возрастать и будет оставаться постоянной, так как поверхностный слой целиком заполнен. Это есть предельная адсорбция — адсорбция в момент образования монослоя адсорбата, состоящего из молекул ПАВ. По значению предельной адсорбции Г^ можно определить параметры адсорбционного слоя: Во — площадь, занимаемую одной молекулой ПАВ, и 5 — толщину адсорбционного слоя (см. рис. 5.2, б). Если обозначить число молекул насыщенного адсорбционного слоя площадью 1м2 через ято, то площадь, занимаемая одной молекулой, будет определяться по формуле Во = Х/п^ = 1/(/jVa), (5.9) где NA — число Авогадро. Зная плотность растворенного вещества р и его молекулярную массу М, можно рассчитать толщину предельного адсорбционного слоя, которая будет соответствовать длине молекул (вследствие вертикальной ориентации молекул в мономолекулярном слое). Произведение Г^М эквивалентно массе адсорбата на 1 м2: моль/м2кг/моль = кг/м2 Эту же массу можно выразить через произведение 5р(м • кг/м3 = кг/м2), т.е. = 5р; 5 = Г^М/р. (5.10) Таким образом, предельная адсорбция позволяет определить размеры молекул ПАВ в насыщенном адсорбционном слое. Предельная адсорбция определяет площадь, занимаемую гидрофильной частью молекул ПАВ, которая не зависит от длины углеводородного радикала, т.е. гидрофобной части молекулы. Так, например, гидрофильная часть алифатических спиртов определяется гидроксильной группой ОН, и их предельная адсорбция (выраженная в молях
на м2) будет одинакова/В соответствии с уравнением (5.9) площадь в адсорбционном слое одной молекулы всех спиртов будет также одинакова и равна 0,25 нм2, или 0,25 • 10~18 м2. Для всех жирных кислот (например, уксусной, пропионовой, масляной, валериановой, капроновой, гептановой), несмотря на различие углеводородной части, площадь поперечного сечения молекул в адсорбционном насыщенном слое составляет 0,20 нм2, или 0,20 • 10~18 м2. По значению предельной адсорбции с помощью уравнений (5.9) и (5.10) в 1919 г. коллоидно-химическими методами впервые удалось определить размеры молекул. По мере развития науки размеры молекул стали определять другими методами, результаты которых подтвердили достоверность полученных ранее данных. Предельную адсорбцию Гж, которая является важнейшей характеристикой мономолекулярной адсорбции, можно определить графическим путем. Для этой цели уравнение (4.34) представляют в следующем виде:
\ + Ьс
(5.11)
Ть + г (5.12) В координатах «1/Т— 1/с» уравнение (5.12) описывается прямой (линия 1 на рис. 5.4). Тангенс угла наклона этой прямой есть величина, обратная предельной адсорбции, т.е. tga = \/FJb. Отрезок, отсекаемый на оси ординат, характеризует величину \/Гх, первое слагаемое правой части уравнения (5.12), т.е. величину, обратную предельной адсорбции, что позволяет найти предельную адсорбцию /\ По тангенсу угла наклона прямой 1 можно определить значение FJb, а по ранее известной 1/Гж — численное значение константы Ь. Так, например, рассчитанные по описанному выше методу значения предельной адсорбции для гексилового СН3(СН2)4СН ОН и гептилового СН3(СН2)5СН2ОН спиртов совпадают и равны 1- 10~~5 моль/м2. Таким образом, по изотерме адсорбции Г =f(c) можно определить не только значение предельной адсорбции, но и константу b уравнения Ленгмюра [уравнение (4.34)]. В соответствии с уравнением (4.29) b характеризует константу равновесия процессов адсорбции и десорбции, когда адсорбция не достигла предельного значения, а снижение поверхностного натяжения определяется поверхностной активностью g [см. формулу (5.1) и рис. 5.1]. Иными словами, константа равновесия адсорбционного процесса связана с поверхностной активностью g. Рассмотрим рис. 5.5. На рис. 5.5, а изображены изотермы адсорбции, а на рис. 5.5, б показано снижение поверхностного натяжения по мере увеличения концентрации пропилового С3Н7ОН (кривая 1), бутилового С4Н9ОН (кривая 2) и пентилового С5НПОН (кривая 3) спиртов. Поверхностная активность g в соответствии с формулой (5.1) есть производная функции da/dc при с —> 0 и определяется тангенсом угла наклона кривых /, 2 и 3. Поверхностная активность различных спиртов неодинакова; из рис. 5.5, б следует, что —tga3 > —tga2 > —tga,, (da/dc)3 > (da/dc)2 ,; g3 > g2> (5.13)
Рис. 5.4. Графическое
определение Г. [к уравнению (15.12)]
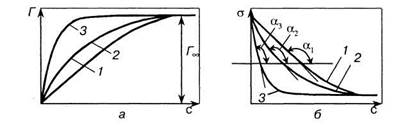
Условие (5.13) означает, что с увеличением длины углеводородного радикала, характеризующего гидрофобную часть молекулы ПАВ, поверхностная активность увеличивается. Чем больше величина поверхностной активности, тем круче изотерма адсорбции (сравним кривые 1 и 3 на рис. 5.5, а) и быстрее достигается предельная адсорбция.
Поверхностная активность зависит от длины углеводородного радикала, и согласно эмпирическому правилу Траубе-Дюкло при удлинении углеводородного радикала на одно звено (группу) СН2 поверхностная активность увеличивается примерно в 3—3,5 раза. Это правило соблюдается для водных растворов некоторых ПАВ при небольшой длине углеводородного радикала и комнатной температуре. Константа Ь, входящая в уравнение (4.34), увеличивается (как и поверхностная активность) примерно в 3—3,5 раза при удлинении на одну группу СН2 углеводородной части молекул ПАВ данного гомологического ряда. Константа b для гексилового спирта С6Н13ОН равна 1,1 • 10~3, а для гептилового С7Н15ОН — 3,3 • 10~3, т.е. увеличивается в 3,3 раза при удлинении углеводородной цепи на одну группу СН2; в данном случае соблюдается правило Дюкло-Траубе. Гидрофобные взаимодействия Термин «гидрофобные взаимодействия» был предложен Лен-гмюром еще в 1916 г. при выводе уравнения изотермы мономолекулярной адсорбции. Они возникают только в водных растворах в результате взаимодействия полярных молекул воды с неполярными гидрофобными частицами, молекулами (углеводородами) или неполярными радикалами молекул, в частности неполярными радикалами молекул ПАВ.
Фундаментальное уравнение адсорбции Гиббса Адсорбция относится к поверхностным явлениям и протекает самоЬроиЗвольно. Концентрация веществ на поверхности раздела фаз происходит до достижения равновесия между процессами адсорбции и десорбции (см. рис. 4.1). Для нахождения условий протекания самопроизвольного равновесного процесса обратимся к основам химической термодинамики. Адсорбция идет самопроизвольно, когда имеет место уменьшение энергии Гиббса, т.е. dC < 0. Согласно условию (2.1) для изобарно-изотермического процесса в отсутствие изменений площади поверхности раздела фаз и заряда поверхности (6Т = О, dp = О, dB = О и dq = 0) можно записать
dG< Для однокомпонентной системы получим dG<Ajnd«, или AG < A\idn. (4.7) Если обозначить химический потенциал /-го компонента в объеме адсорбтива через (\x.v) и на поверхности адсорбента (ц.*), то согласно согласно (4.7) изменение энергии Гиббса определится по формуле; AG < (iiB - ^)dnf. (4.8) Для самопроизвольных процессов (dG < 0) из условия (4.8) получим цГ>цД (4.9)
Химический потенциал является фактором интенсивности любого физико-химического процесса, в том числе и адсорбции. Согласно условию (4.9) химический потенциал вещества в объе- превышает химический потенциал этого же вещества на поверхности \х Процесс адсорбции будет протекать до тех пор, пока будут достигнуты равновесные условия, т.е. до достижения состояния, когда AG = 0, что, согласно условию (4.8), соответствует равенству химических потенциалов адсорбтива и адсорбата (ц.к= ju/6). В условиях равновесия скорости адсорбции и десорбции становятся равными. На основании этого адсорбцию можно определить как процесс выравнивания химического потенциала, приводящего к росту концентрации компонентов на границе раздела фаз по сравнению с их концентрацией в объеме.
В случае адсорбции только одного компонента уравнение (4.13) упрощается:
-da = /Иц; Г = -da/dju.
(4.10) Это уравнение связывает поверхностное натяжение с процессами, протекающими на границе раздела фаз. В нем экстенсивные величины стоят под знаком дифференциала (dni и dB). Для однородной функции первой степени относительно экстенсивных величин можно воспользоваться теоремой Эйлера, которая позволяет интегрировать это уравнение при постоянных значениях коэффициентов интенсивных величин (\х. и а) при дифференциалах. Напомним, что согласно теореме Эйлера любая однородная функция степени к, имеющая непрерывные частные производные, удовлетворяет равенству fx(x,y,z)x-+fy(x,y,z)y +fz(x,y,z)z=kj{x,y,z). Однородной называется функция, если при умножении всех ее аргументов на множитель она приобретает этот же множитель в к-й степени, т.е. Atxr..., txj = f(xp..., xj. Таким образом, если состав поверхностного слоя не изменяется, что соответствует конечному значению В и п., то можно записать (4.10, а) Полный дифференциал от всех переменных уравнения (4.10, а) выглядит так: Уравнения (4.13) и (4.14) справедливы для всех видов адсорбции; они показывают, что при адсорбции происходит самопроизвольное снижение удельной свободной поверхностной энергии (поверхностного натяжения) по мере изменения химического потенциала. Адсорбция определяется избытком концентрации адсорбива с и обусловлена изменением поверхностного натяжения а, которое зависит от температуры (см. параграф 2.3). Все величины, определяющие адсорбцию, взаимосвязаны, т.е. Г=/(с, а, 7). Для нахождения этой зависимости воспользуемся уравнениями (4.13), в которых da характеризует уменьшение поверхностного натяжения в результате самопроизвольного процесса при адсорбции; Г. определяет адсорбцию количественно, а dju. показывает возможность и интенсивность самопроизвольного процесса в результате изменения химического потенциала. Используя уравнения (4.13), определим адсорбцию одного i- го компонента из смеси веществ:
Г. = - (Эа/Эц.) Адсорбция одного компонента /согласно условию (4.15) есть частная производная от поверхностного натяжения (удельной свободной поверхностной энергии) по изменению химического потенциала при постоянных химических потенциалах других компонентов. Для нахождения химического потенциала воспользуемся следующим соотношением:
И,- <Ц + S л, Ф, + odB + Bdo = 0. ' 1 Из уравнения (4.11) вычтем уравнение (4.10), в результате получим Х2/Фг (4.12) Используя уравнение (4.4) для выражения адсорбции, вместо формулы (4.12) можно записать -da=5>M; S^^-da/Sdn, (4.13) г =1 i =1 i =1 Это уравнение называют фундаментальным уравнением адсорбции Гиббса.
RTlnc, где ц,., ц/3 — равновесный и стандартный химический потенциал адсорбтива; с — концентрация адсорбтива. Если адсорбтив является сильным электролитом и его концентрация значительна, то вместо концентрации в этом уравнении следует использовать активность а. Дифференцируя уравнение (4.16) и учитывая, что jn;° есть величина постоянная, получим djLX. = RTdlnc = RT{dc/c). (4.17) Заменив d^i. в уравнении (4.13), подставив полученное выражение для d\x. в уравнение (4.17), получим Г= ~ (c/RT)(da/dc). (4.18)
3—766
Уравнение (4.18) непосредственно следует из фундаментального уравнения адсорбции Гиббса (4.14) и характеризует влияние на избыточную адсорбцию концентрации адсорбтива и температуры, а также изменение поверхностного натяжения (удельной свободной поверхностной энергии) в зависимости от концентрации адсорбтива. Оно справедливо для всех видов адсорбции. Таким образом, уравнение (4.18) связывает между собой основные параметры, характеризующие адсорбцию (Г, с, Ти а), и определяет результат самопроизвольного процесса за счет снижения поверхностного натяжения. Обычно рассматривают зависимость адсорбции от концентрации адсорбтива, что и будет использовано в дальнейшем.
|
|||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2017-02-10; просмотров: 619; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.17.165.196 (0.014 с.) |

 Так как ]ы.к < \itB, самопроизвольно будет протекать десорбция.
Так как ]ы.к < \itB, самопроизвольно будет протекать десорбция.


 Г Г„Ъс Г ГЬс ГЪс
Г Г„Ъс Г ГЬс ГЪс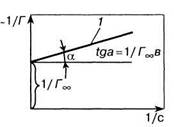
 Для изобарно-изотермического процесса, когда <\Т = 0, dp = О, dq = О, с учетом всех компонентов системы в условиях равновесия (dG = 0) из уравнения (2.1) получим
Для изобарно-изотермического процесса, когда <\Т = 0, dp = О, dq = О, с учетом всех компонентов системы в условиях равновесия (dG = 0) из уравнения (2.1) получим