
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Формула полной вероятности. Формула БайесаСодержание книги Похожие статьи вашей тематики
Поиск на нашем сайте
Определение полной группы событий. Полной группой Полная группа событий (гипотез) должна иметь отношение к рассматриваемому испытанию, при котором возможно некоторое случайное событие Формула полной вероятности. Формула Байеса.
Задача 12. Три завода выпускают один вид продукции. Объемы выпуска заводов относятся как 2: 3: 5. Доля некачественной продукции для заводов составляет, соответственно, N, N+5, N+10 процентов (N-номер варианта). Продукция поступает на общий склад, с которого произвольно распределяется по торговым точкам. Найти вероятность, что купленная единица продукции окажется некачественной. Купленная единица продукции оказалась качественной, найти вероятность ее изготовления на том или ином заводе.
Пример решения задачи 12. Три завода выпускают один вид продукции. Объемы выпуска заводов относятся как 1: 2: 3. Доля некачественной продукции для заводов составляет, соответственно, 0,1; 0,4; 0,2 процентов. Продукция поступает на общий склад, с которого произвольно распределяется по торговым точкам. 1) Найти вероятность, что купленная единица продукции окажется некачественной. 2) Купленная единица продукции оказалась качественной, найти вероятность ее изготовления на том или ином заводе.
Решение: Определим случайные события:
Гипотезы
Здесь 1) Применяя формулу полной вероятности, получаем
Заметим, что требование полноты на языке вероятности можно записать как
2) Поскольку для противоположных событий имеет место свойство
найдем вероятность покупки единицы качественной продукции
Найдем теперь, что эта единица качественной продукции куплена на заводе №1, №2, №3. Применяем для этого трижды формулу Байеса:
Здесь опять было использовано свойство для противоположных событий, но которое теперь записывалось в форме:
В качестве проверки 2) части примера можно сложить три последние условные вероятности, сумма должна равняться единице ввиду полноты полной группы событий. Задача 13. Надежность работы (вероятность безотказной работы) каждого станка первой экспериментальной партии станков равна N/(N+5). Найти вероятность, что из десяти станков выйдут из строя: а) пять станков; б) не более трех станков; в) все станки; г) хотя бы один станок.
Пример решения задачи 13. Надежность работы (вероятность безотказной работы) каждого прибора равна 0,2. Найти вероятность, что из пяти приборов выйдут из строя: а) два; б) не более трех; в) все; г) хотя бы один. Решение: Решение проводим с помощью формулы Бернулли:
Интересующее нас случайное событие
a) Найдем вероятность, что из пяти приборов при их испытании надежно работать будут только два прибора (cобытие A наступит только два раза)
б) Найдем вероятность, что из пяти приборов при их испытании надежно работать будут не более трех приборов. Поскольку при этом
где
в) Найдем вероятность, что из пяти приборов при их испытании надежно работать будет все приборы. Поскольку при этом
г) Найдем вероятность, что из пяти приборов при их испытании надежно работать будет хотя бы один прибор. Поскольку при этом
Тогда искомая вероятность могла бы быть найдена аналогично случаю б) как
Однако мы поступим иначе и вычислим искомую вероятность не таким громоздким методам. Действительно, используя уже вычисленное значение
СЛУЧАЙНЫЕ ВЕЛИЧИНЫ Определение дискретной случайной величины. Дискретной случайной величиной
Задача 14*. Баскетболист бросает мяч в корзину до первого попадания. Вероятность попасть в корзину при каждом броске считать постоянной и равной N/(N+5). Найти закон распределения случайной величины числа бросков. Найти математическое ожидание числа бросков. (Воспользоваться методом интегрирования степенных рядов. См задачу 15 Задания Интегрирование). Пример решения задачи 14*. Футболист бьет мяч по воротам до первого попадания. Вероятность забить гол при каждом ударе постоянна и равна 0,2. Найти закон распределения случайной величины Решение: Введем систему элементарных несовместных случайных событий:
Тогда значения случайной величины
Вероятности этих значений случайной величины находим по формуле вероятности произведения несовместных случайных событий
Таким образом, закон распределения случайной величины
Найдем математическое ожидание случайной величины
Здесь сумма ряда, стоящего в скобках обозначена как
Для нахождения суммы числового ряда (1) сначала вместо 0,8 поставим значение x, тогда получается степенной ряд (2):
при этом очевидно равенство
Сравним ряд (2) с известным сходящимся рядом (4)
который представляет собой сумму бесконечно убывающей геометрической прогрессии со знаменателем Проинтегрируем почленно ряд (2) по области его сходимости
и после интегрирования получаем
Сравнивая полученный результат с формулой (4), получаем равенство
Полученное равенство представляет собой интегральное уравнение относительно неизвестной функции
откуда получаем необходимое значение
Таким образом, искомое математическое ожидание случайной величины
И, следовательно, по смыслу математического ожидания, в среднем наш футболист для попадания в ворота должен сделать пять попыток. Убедимся теперь, что найденный выше закон распределения случайной величины
Действительно, имеем равенство
что и доказывает выполнимость указанного свойства. Здесь была использована формула (4) для суммы бесконечно убывающей геометрической прогрессии. Задача 15. Группа из 30 студентов сдала экзамен. Для случайной величины X– полученной на экзамене оценки наудачу выбранным студентом, имеет место закон распределения (N- номер варианта)
Найти, округляя, a) число студентов, получивших те или иные оценки; б) средний балл на экзамене; с) математическое ожидание и дисперсию случайной величины X.
Пример решения задачи 15. В группе из 100 человек для случайной величины X–цвет волос наудачу выбранного человека, имеет место закон распределения
Найти, округляя, a) число человек с тем или иным цветом волос; б)в среднем каков цвет волос у членов группы?; с) математическое ожидание и дисперсию случайной величины X.
Решение: а) По смыслу вероятности, распределение людей по цвету волос представим таблицей
б) В среднем цвет волос характеризуется математическим ожиданием случайной величины X:
Другими словами «средний» цвет волос – чуть темнее желтого. с) Дисперсию найдем по упрощенной формуле, учитывая, что математическое ожидание случайной величины уже найдено
Найдем среднее значение квадрата случайной величины
Подставляя найденное значение в формулу для дисперсии, окончательно получаем
Определение непрерывной случайной величины. Непрерывной случайной величиной Вероятность же попасть в конечный интервал Имеет место условие нормировки вероятности на единицу: Вероятность попасть в конечный интервал
Задача 16. Для непрерывной случайной величины Х, имеющей плотность распределения a) нормировочную постоянную b) функцию распределения c) построить графики плотности и функции распределения d) математическое ожидание и дисперсию случайной величины Х; e) вероятность попадания случайной величины Х в интервал
Пример решения задачи 16. Для непрерывной случайной величины Х, имеющей плотность распределения a) нормировочную постоянную b) функцию распределения c) Построить графики плотности и функции распределения; d) математическое ожидание и дисперсию случайной величины Х; e) вероятность попадания случайной величины Х в интервал -
Решение: a) Для нахождения нормировочной постоянной A нужно воспользоваться условием нормировки вероятности на единицу, что соответствует площади по кривой
Таким образом нормировочная постоянная
При этом плотность распределения оказывается равной
b) По определению функцией распределения называется величина
и поскольку 1)Так для первого участка
2) Для второго участка
3) Для третьего участка
4) И, наконец, для четвертого участка
С учетом выражений (8-11) функция распределения окончательно может быть записаны в виде кусочной функции
c) Построим графики плотности и функции распределения
0,5
-1 2 х
-1 2 х d) Найдем математическое ожидание случайной величины Х; Для непрерывной случайной величины, какой и является величинв X, математическое ожидание находим, используя ее определение:
Найдем дисперсию случайной величины Х. Несмотря на то, что случайная величина X является непрерывной величиной формула для дисперсии остается прежней:
Найдем среднее значение квадрата случайной величины, теперь с учетом непрерывности случайной величины, используем формулу
Теперь окончательно получаем значение дисперсии случайной величины
e) Находим вероятность попадания случайной величины Х в интервал
Задача 17. Для непрерывной случайной величины Х, имеющей функцию распределения где a) нормировочную постоянную b) вероятность попадания случайной величины Х в интервал с) плотность распределения d) построить графики функций e) математическое ожидание и дисперсию случайной величины Х;
Пример решения задачи 17. Для непрерывной случайной величины Х, имеющей функцию распределения найти: a) нормировочную постоянную b) вероятность попадания случайной величины Х в интервал c).плотность распределения d) построить графики функций е) математическое ожидание и дисперсию случайной величины Х. Решение: a) Для нахождения нормировочной постоянной A воспользуемся свойством функции распределения
откуда необходимо положить
Таким образом, функция распределения приобретает окончательный вид
b) Найдем вероятность попадания случайной величины Х в интервал
Таким для искомой вероятности получаем значение:
c). Для нахождения плотности распределения
тогда, дифференцируя каждую ветвь функции распределения
График функции распределения
х
e) Математическое ожидание и дисперсию случайной величины Х может быть найдена как и в предыдущем примере с помощью плотности распределения
Интеграл может быть вычислен методом интегрирования по частям в соответствии с формулой
То, что математическое ожидание (среднее значение случайной величины) равно Дисперсию X будем опять находить по формуле
Среднее значение квадрата случайной величины найдем отдельно:
Интеграл вычисляется двукратным интегрированием по частям:
Подставляя найденную величину, получаем окончательно значение дисперсии случайной величины X:
· Дискретные двумерные случайные величины Двумерная случайная величина
Каждая их компонент
со своими числовыми характеристиками
Если компоненты
Для зависимых компонент
где условный закон распределения
Аналогично для условного закона распределения
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2017-02-08; просмотров: 718; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.189.182.15 (0.014 с.) |

 случайных событий называется такая совокупность попарно несовместных случайных событий, т.е.
случайных событий называется такая совокупность попарно несовместных случайных событий, т.е.  при
при  которая, кроме того - полна, т.е. имеет место равенство
которая, кроме того - полна, т.е. имеет место равенство  (На языке вероятности, что эквивалентно:
(На языке вероятности, что эквивалентно:  при
при  ).
). , происходящее только одновременно с одним из событий
, происходящее только одновременно с одним из событий 
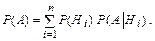

 купленная единица продукции окажется некачественной.
купленная единица продукции окажется некачественной.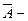 купленная единица продукции окажется некачественной.
купленная единица продукции окажется некачественной. , образуют полную группу событий, т.е. они должны удовлетворять двум требованиям (требование полноты и попарной несовместности):
, образуют полную группу событий, т.е. они должны удовлетворять двум требованиям (требование полноты и попарной несовместности): ,
, 
 купленная единица продукции изготовлена на заводе №1;
купленная единица продукции изготовлена на заводе №1; купленная единица продукции изготовлена на заводе №2;
купленная единица продукции изготовлена на заводе №2; купленная единица продукции изготовлена на заводе №3.
купленная единица продукции изготовлена на заводе №3. достоверное событие; - невозможное случайное событие
достоверное событие; - невозможное случайное событие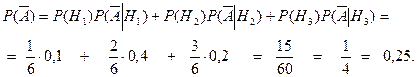
 .
.



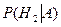

 .
. .
.

 , искомое событие
, искомое событие  (надежная работа не более трех приборов) представим суммой несовместных случайных событий
(надежная работа не более трех приборов) представим суммой несовместных случайных событий ,
, надежная работа приборов в количестве i штук. Тогда Искомая вероятность
надежная работа приборов в количестве i штук. Тогда Искомая вероятность
 , искомая вероятность
, искомая вероятность
 , искомое событие
, искомое событие  (надежная работа хотя бы одного прибора) представим суммой несовместных случайных событий
(надежная работа хотя бы одного прибора) представим суммой несовместных случайных событий ,
,
 в пункте а), имеет место равенство
в пункте а), имеет место равенство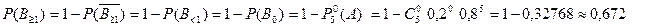
 называется величина, принимающая в результате испытания дискретные значения
называется величина, принимающая в результате испытания дискретные значения  , каждое из которых является случайным событием. Как следствие
, каждое из которых является случайным событием. Как следствие 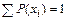 .
. – числа выполненных ударов. Найти математическое ожидание числа выполненных ударов.
– числа выполненных ударов. Найти математическое ожидание числа выполненных ударов. футболист забивает мяч при k-ом ударе;
футболист забивает мяч при k-ом ударе; футболист не забивает мяч при k-ом ударе.
футболист не забивает мяч при k-ом ударе. , представляющие собой случайные события- возможное число ударов мяча (индекс соответствует числу выполненных ударов) можно выразить через элементарные события в виде
, представляющие собой случайные события- возможное число ударов мяча (индекс соответствует числу выполненных ударов) можно выразить через элементарные события в виде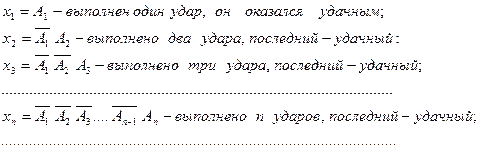
 .
.









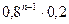



 .
. . (1)
. (1) (2)
(2) . (3)
. (3)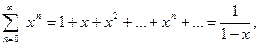 (4)
(4) .
.

 . (5)
. (5) . (6)
. (6) , которую легко можно найти, продифференцировав равенство:
, которую легко можно найти, продифференцировав равенство: ,
, .
. .
. . (7)
. (7)
 ,
, .
.

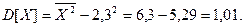
 называется величина, принимающая в результате испытания свои значения из заданного интервала
называется величина, принимающая в результате испытания свои значения из заданного интервала  . Вероятность, что значения
. Вероятность, что значения  в окрестности точки
в окрестности точки  , определяется плотностью вероятности
, определяется плотностью вероятности  и имеет вид
и имеет вид  .
. тогда можно представить как
тогда можно представить как 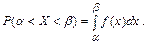
 . Границы интервала
. Границы интервала  как
как  где
где 
 где
где 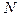 - номер варианта, найти:
- номер варианта, найти:



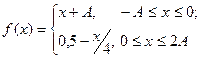 найти:
найти: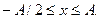
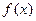 , равной единице. Таким образом, имеем равенство
, равной единице. Таким образом, имеем равенство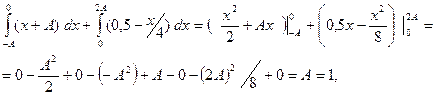

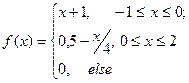 .
. ,
, плотность распределения является кусочной функцией, состоящей из четырех участков
плотность распределения является кусочной функцией, состоящей из четырех участков  , для каждого участка найдем значение функции распределения:
, для каждого участка найдем значение функции распределения: функция распределения равна:
функция распределения равна:
 функция распределения равна:
функция распределения равна:
 функция распределения равна:
функция распределения равна:

 функция распределения равна:
функция распределения равна:


 f(x) График плотности распределения
f(x) График плотности распределения



 F(x) График функции распределения
F(x) График функции распределения





 0,5
0,5










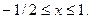 Эта вероятнось равна площади под кривой плотности распределения
Эта вероятнось равна площади под кривой плотности распределения 


 ,
, номер варианта, найти:
номер варианта, найти: ;
; .
.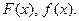
 ,
,
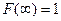 ,
,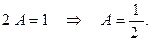
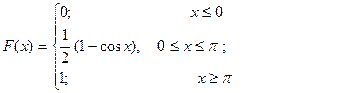
 . Используя свойство функции распределения можно
. Используя свойство функции распределения можно 

 , связывающим обе функции:
, связывающим обе функции:

 d) построим графики функций
d) построим графики функций 



 1
1


 х
х

 .
. :
:
 можно было ожидать исходя из рисунка плотности распределения
можно было ожидать исходя из рисунка плотности распределения 
 .
.

 задается своим законом распределения
задается своим законом распределения .
. имеет свой закон распределения
имеет свой закон распределения ,
, .
. -,
-,  -математическими ожиланиями,
-математическими ожиланиями,  -дисперсиями,
-дисперсиями,  -среднеквадратическими отклонениями
-среднеквадратическими отклонениями ;
; .
. независимы, то
независимы, то
 .
. ,
, при условии
при условии  можно представить как
можно представить как ,
,  .
. получаем
получаем ,
, ,
,  .
.


