
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Сборник типовых заданий по высшей математикеСодержание книги Поиск на нашем сайте
Д. Н. КАЧЕВСКИЙ
ТЕОРИЯ ВЕРОЯТНОСТЕЙ
СБОРНИК ТИПОВЫХ ЗАДАНИЙ ПО ВЫСШЕЙ МАТЕМАТИКЕ
Учебное пособие для студентов вузов Экономических и технических специальностей Издание второе
Чебоксары «ДНК» 2008
К 30 УДК 517.3 Качевский Дмитрий Николаевич К 30 Теория вероятностей. Сборник типовых заданий по высшей математике,- Чебоксары: ДНК, 2008, 36 с., ил. Учебное пособие по высшей математике для студентов вузов экономических и технических специальностей. Содержит типовые контрольные задания по теории вероятностей для самостоятельной работы. Задания разбиты по вариантам и включают разделы: случайные события, случайные величины. Каждая задача снабжена примером решения. Для основных понятий дается краткая теоретическая справка. Пособие может быть использовано студентами всех форм обучения.
© Чебоксары, «ДНК», 2008.
Предисловие ко второму изданию Учебное пособие предназначено для самостоятельной работы студентов вузов технических и экономических специальностей всех форм обучения. Предлагаются типовые задания в 10 вариантах по теории вероятностей с примерами решения задач.
СЛУЧАЙНЫЕ СОБЫТИЯ Алгебра случайных событий Определение случайного события. Случайное событие Определение противоположного случайного события. Противоположноеслучайное событие Определение невозможного случайного события. Невозможное случайное событие – это такое событие, которое не может произойти в результате испытания. Определение достоверного случайного события. Достоверное случайное событие Определение произведения случайных событий. Случайное событие Определение суммы случайных событий. Случайное событие
либо только событие либо только событие либо одновременно и событие в результате некоторого испытания Свойства случайных событий 1° 2° 3° 4° 5° 6° 7° 8° 9°
11° Задача 0. Придумать оригинальную задачу с заданными случайными событиями, с помощью которых определить все неизвестные случайные события. Примеры решения задача 0. Пример 01. С самолета сбрасываются на наземную цель две бомбы. Цель считается разрушенной, если в нее попала хотя бы одна бомба. Для заданных случайных событий: Решение примера 01. По условию задачи и с учетом определения суммы случайных событий имеем равенство Пример 02. Футболист трижды бьет по воротам. Для заданных случайных событий: Решение примера 02.
Пример 03. Два игрока Антон и Борисподбрасывают игральную кость (шестигранный куб со значениями граней от 1 до 6). Для заданных случайных событий Решение примера 03. С учетом имеющихся четырех вариантов получения суммы очков, равной пяти имеем искомое равенство
0,5
-1 2 х
-1 2 х d) Найдем математическое ожидание случайной величины Х; Для непрерывной случайной величины, какой и является величинв X, математическое ожидание находим, используя ее определение:
Найдем дисперсию случайной величины Х. Несмотря на то, что случайная величина X является непрерывной величиной формула для дисперсии остается прежней:
Найдем среднее значение квадрата случайной величины, теперь с учетом непрерывности случайной величины, используем формулу
Теперь окончательно получаем значение дисперсии случайной величины
e) Находим вероятность попадания случайной величины Х в интервал
Задача 17. Для непрерывной случайной величины Х, имеющей функцию распределения где a) нормировочную постоянную b) вероятность попадания случайной величины Х в интервал с) плотность распределения d) построить графики функций e) математическое ожидание и дисперсию случайной величины Х;
Пример решения задачи 17. Для непрерывной случайной величины Х, имеющей функцию распределения найти: a) нормировочную постоянную b) вероятность попадания случайной величины Х в интервал c).плотность распределения d) построить графики функций е) математическое ожидание и дисперсию случайной величины Х. Решение: a) Для нахождения нормировочной постоянной A воспользуемся свойством функции распределения
откуда необходимо положить
Таким образом, функция распределения приобретает окончательный вид
b) Найдем вероятность попадания случайной величины Х в интервал
Таким для искомой вероятности получаем значение:
c). Для нахождения плотности распределения
тогда, дифференцируя каждую ветвь функции распределения
График функции распределения
х
e) Математическое ожидание и дисперсию случайной величины Х может быть найдена как и в предыдущем примере с помощью плотности распределения
Интеграл может быть вычислен методом интегрирования по частям в соответствии с формулой
То, что математическое ожидание (среднее значение случайной величины) равно Дисперсию X будем опять находить по формуле
Среднее значение квадрата случайной величины найдем отдельно:
Интеграл вычисляется двукратным интегрированием по частям:
Подставляя найденную величину, получаем окончательно значение дисперсии случайной величины X:
· Дискретные двумерные случайные величины Двумерная случайная величина
Каждая их компонент
со своими числовыми характеристиками
Если компоненты
Для зависимых компонент
где условный закон распределения
Аналогично для условного закона распределения
Табл.1
Сразу найдем числовые характеристики компоненты Х: Математическое ожидание X: Дисперсия Х: Среднее квадратическое отклонение: Закон распределения компоненты Y получаем суммированием вероятностей двумерной случайной величины Z=(X, Y) по строкам: Табл.2
Убеждаемся, что сумма вероятностей равна единице, как и должно быть для дискретных законов распределения. Найдем числовые характеристики компоненты Y: Математическое ожидание Y: Дисперсия Y: Среднее квадратическое отклонение: b) Выясним, зависят ли друг от друга компоненты Х и Y. Предположим, что компоненты не зависят друг от друга, тогда вероятность значения двумерной случайной величины
в этом случае закон распределения двумерной случайной величины должен бы иметь вид (используем Табл. 1, и Табл.2)
Закон распределения
Сравнивая полученный закон распределения величины c) Найдем условные законы распределения компоненты Y при фиксированных значениях компоненты X: Табл. 3
Сразу найдем условное математическое ожидание Y при
Табл. 4
Найдем условное математическое ожидание Y при
Табл. 5
Найдем условное математическое ожидание Y при
Тот факт, что таблицы 3, 4, 5 не совпадаю друг с другом еще раз свидетельствуют о зависимости случайных величин друг от друга. d) Найдем регрессию Y на X. Для этого построим график зависимости среднего значения y при фиксированном значении x, т.е. график зависимости условного математического ожидания График регрессии Y на Х
20
-1 0 1 2 x e) Найдем коэффициент корреляции случайных величин Y и X: Коэффициент корреляции
где корреляционный момент может быть найден по формуле
Найдем сначала среднее значение произведения компонент X и Y:
воспользовавшись матрицей вероятностей
откуда для коэффициента корреляции получаем значение
Таким образом, между случайными величинами X и Y имеется достаточно тесная корреляционная связь. Как известно, теснота корреляционной связи определяется тем, насколько коэффициент корреляции отличается по модулю от единицы. Сам же коэффициент корреляции обладает свойством
Чем ближе коэффициент корреляции к единице, тем тесней корреляционная связь компонент X и Y.
Задача 19. Для двумерной случайной величины Z(X, Y) Задачи 18 найти уравнение линейной регрессии Y на Х. График этой регрессии построить в тех же осях и на том же рисунке, что и график самой регрессии Y на Х, построенный в Задаче 18. Сравнить эти графики.
Пример решения задачи 19. Для двумерной случайной величины Z(X, Y) Примера решения задачи 18 найти уравнение линейной регрессии Y на Х. График этой регрессии построить в тех же осях, что и график самой регрессии Y на Х, построенный в Задаче 18. Сравнить эти графики.
Решение: График линейной регрессии Y на X представляет собой тенденцию изменения среднего значения величины Y при фиксированном значении X от этого значения X. Более детальная информацию об этой зависимости при этом теряется. Уравнение линейной регрессии Y на X, которую будем обозначать
и представляет собой канонический вид уравнения прямой на плоскости
При решении Примера18 все эти параметры были найдены: Подставляя их в уравнение линейной регрессии, запишем его в форме
из которой следует, что прямая, проходя через точку A(0,35; 19,5), имеет направляющий вектор График регрессии Y на Х
-1 0 1 2 x То, что регрессия Задача 20. Найти закон распределения случайной величины
Пример решения задачи 20 Найти закон распределения случайной величины
Решение: Числовые характеристики компонент X и Y были найдены в примере 18 и записывались в виде:
Математическое ожидание случайной величины V найдем, воспользовавшись свойствами математического ожидания:
Дисперсию случайной величины V также найдем, воспользовавшись свойствами дисперсии
и свойством корреляционного момента
Дисперсия случайной величины V принимает значение:
или в более простой форме:
Для построения закона распределения случайной величины V=5X+Y учтем, что компоненты X, Y являются зависимыми случайными величинами и появления любой пары их значений, дающих в результате значение величины V, может происходить с вероятность двумерной случайной величины Z=(X,Y)Примера 18:
Закон распределения случайной величины W=5X+Yимеет вид:
Поясним на примере. Так значение Поскольку значения W=25 и W=30 реализуются в испытаниях с вероятностью P=0, т.е. фактически не реализуются (невозможные события). Их можно исключить из закона распределения. Закон распределения случайной величины V=5X+Y, таким образом,имеет вид:
Найдем числовые характеристики случайной величины W, используя их определение и полученный закон распределения. Математическое ожидание V:
Дисперсия W:
Как видим, оба способа вычисления числовых характеристик случайной величины V дают один и тот же результат. Задача 21. Из 20-50 знакомых сверстников (ровесников, соучеников и прочих формальных или неформальных объединений, групп), образующих некоторую выборку, построить вариационный ряд для какого-либо параметра
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2017-02-08; просмотров: 245; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.143.247.108 (0.011 с.) |


 – это такое событие, которое может произойти, а может и не произойти в результате испытания.
– это такое событие, которое может произойти, а может и не произойти в результате испытания. – это такое событие, которое заключается в том, что в результате испытания событие
– это такое событие, которое заключается в том, что в результате испытания событие  – это такое событие, которое обязательно происходит в результате испытания.
– это такое событие, которое обязательно происходит в результате испытания. , равное произведению двух случайных событий
, равное произведению двух случайных событий  и
и 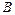 - есть такое событие, которое заключается в том, что в результате испытания происходит и событие
- есть такое событие, которое заключается в том, что в результате испытания происходит и событие  , равное сумме двух случайных событий
, равное сумме двух случайных событий 


 =,
=,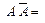 ,
, 


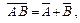
 =A,
=A, 10°
10°  ,
, 


 - первая бомба попала в цель,
- первая бомба попала в цель, 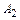 - вторая бомба попала в цель, найти случайные события
- вторая бомба попала в цель, найти случайные события 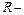 цель разрушена и
цель разрушена и 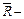 цель не разрушена.
цель не разрушена. Для определения
Для определения 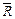 воспользуемся свойством 7°:
воспользуемся свойством 7°: 
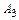 - третий первый мяч попал в ворота, найти случайные события
- третий первый мяч попал в ворота, найти случайные события  ни один мяч в ворота не попал, и
ни один мяч в ворота не попал, и 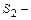 в ворота попали только два мяча,
в ворота попали только два мяча,  в ворота попали только первый и третий мячи.
в ворота попали только первый и третий мячи. поскольку имеются три промаха.
поскольку имеются три промаха. 
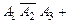
 , поскольку при двух попаданиях возможны три несовместных события: только первый мяч прошел мимо ворот, только второй мяч прошел мимо ворот и только третий мяч прошел мимо ворот.
, поскольку при двух попаданиях возможны три несовместных события: только первый мяч прошел мимо ворот, только второй мяч прошел мимо ворот и только третий мяч прошел мимо ворот.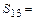
 , случай соответствует только одной возможности – промаху только второго мяча.
, случай соответствует только одной возможности – промаху только второго мяча. Антон получает
Антон получает  очков,
очков,  Борис получает
Борис получает  , найти случайное событие
, найти случайное событие  сумма полученных очков равна пяти.
сумма полученных очков равна пяти.

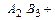
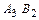 .
.

 F(x) График функции распределения
F(x) График функции распределения





 0,5
0,5
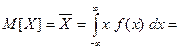











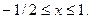 Эта вероятнось равна площади под кривой плотности распределения
Эта вероятнось равна площади под кривой плотности распределения 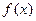 на интервале
на интервале 


 ,
, номер варианта, найти:
номер варианта, найти: ;
; .
.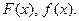
 ,
,
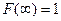 ,
,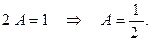
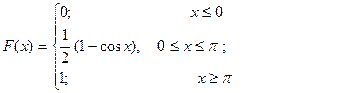
 . Используя свойство функции распределения можно
. Используя свойство функции распределения можно 

 , связывающим обе функции:
, связывающим обе функции:

 d) построим графики функций
d) построим графики функций  F(x)
F(x) 



 1
1


 х
х

 .
. :
:
 можно было ожидать исходя из рисунка плотности распределения
можно было ожидать исходя из рисунка плотности распределения 
 .
.

 задается своим законом распределения
задается своим законом распределения .
. имеет свой закон распределения
имеет свой закон распределения ,
, .
. -,
-,  -математическими ожиланиями,
-математическими ожиланиями,  -дисперсиями,
-дисперсиями,  -среднеквадратическими отклонениями
-среднеквадратическими отклонениями ;
; .
. независимы, то
независимы, то
 .
. ,
, при условии
при условии  можно представить как
можно представить как ,
,  .
. при условии
при условии 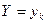 получаем
получаем ,
,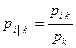 ,
,  .
.
 = -1
= -1
 =0
=0
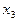 =2
=2

 .
. .
.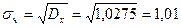 .
.

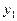 =10
=10
 =20
=20
 =30
=30
 .
. .
. .
. должна являться произведение соответствующих вероятностей компонент, т.е.
должна являться произведение соответствующих вероятностей компонент, т.е. ,
,



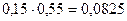

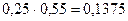





 взяты из первого столбца заданного закона распределения Z(X, Y), а
взяты из первого столбца заданного закона распределения Z(X, Y), а  сумма по столбцу
сумма по столбцу



 :
: .
.
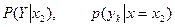
 взяты из второго столбца заданного закона распределения Z(X, Y), а
взяты из второго столбца заданного закона распределения Z(X, Y), а  сумма по столбцу
сумма по столбцу



 :
: .
.

 взяты из второго столбца заданного закона распределения Z(X, Y), а
взяты из второго столбца заданного закона распределения Z(X, Y), а  сумма по столбцу
сумма по столбцу



 :
: .
. от
от  :
:


 30
30 



 определяется как
определяется как ,
, .
.
 заданного закона распределения двумерной случайной величины Z(X, Y)). Тогда коэффициент корреляции будет равен
заданного закона распределения двумерной случайной величины Z(X, Y)). Тогда коэффициент корреляции будет равен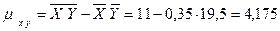 ,
, .
. .
.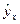 , имеет вид:
, имеет вид: ,
, , здесь
, здесь  математические ожидания компонент X и Y, соответственно;
математические ожидания компонент X и Y, соответственно; их средние квадратические отклонения;
их средние квадратические отклонения; коэффициент корреляции компонент.
коэффициент корреляции компонент.
 ;
;  ;
;  .
. ,
,
 (см. предыдущий Пример) и график линейной регрессии Y на Х
(см. предыдущий Пример) и график линейной регрессии Y на Х 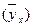 практически совпадают
практически совпадают
 20
20

 A
A

 , которая является по определению прямой, совпадают.
, которая является по определению прямой, совпадают. и ее числовые характеристики, если случайных величин X и Y, являются компонентами двумерной случайной величины Z(X, Y) Задачи 18. Числовые характеристики найти двумя методами: с помощью свойств числовых характеристик и по определению.
и ее числовые характеристики, если случайных величин X и Y, являются компонентами двумерной случайной величины Z(X, Y) Задачи 18. Числовые характеристики найти двумя методами: с помощью свойств числовых характеристик и по определению. и ее числовые характеристики, если случайных величин X и Y, являются компонентами двумерной случайной величины Z(X, Y) Примере 18. Числовые характеристики найти двумя методами: с помощью свойств числовых характеристик и по определению.
и ее числовые характеристики, если случайных величин X и Y, являются компонентами двумерной случайной величины Z(X, Y) Примере 18. Числовые характеристики найти двумя методами: с помощью свойств числовых характеристик и по определению.

 .
. .
.
 постоянные)
постоянные) .
. ,
,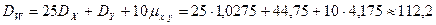 .
. , которая задается матрицей вероятности
, которая задается матрицей вероятности может быть реализовано в испытании, только когда значение X=-1, а значение Y=10, вероятность их совместного появления соответствует вероятности P=0,1.
может быть реализовано в испытании, только когда значение X=-1, а значение Y=10, вероятность их совместного появления соответствует вероятности P=0,1. .
.
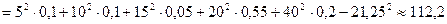 .
. по выборочной средней при помощи доверительного интервала и дисперсию
по выборочной средней при помощи доверительного интервала и дисперсию  этого распределения с надежность 0,95. Оценить вероятность, что наудачу
этого распределения с надежность 0,95. Оценить вероятность, что наудачу 


