
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Вероятность произведения случайных событийСодержание книги Поиск на нашем сайте
где В частности, если события
Задача 6. Вероятности срыва плана тремя предприятиями соответственно равны N/(N+30); (N+2)/(N+30); (N+3)/(N+30). Найти вероятность, что а) ни одно предприятие не сорвало план; б) первое сорвало, второе нет; в) первое сорвало, второе нет, третье сорвало; г) второе и третье сорвали план.
Пример решения задачи 6. Вероятности срыва плана тремя предприятиями соответственно равны 0,1; 0,2; 0,3. Найти вероятность, что а) ни одно предприятие не сорвало план; б) первое сорвало, второе нет; в) первое сорвало, второе нет, третье сорвало; г) второе и третье сорвали план. Решение: Введем элементарные случайные события:
Соответствующие им противоположные элементарные события:
Тогда интересующими нас событиями для рассматриваемых случаев а),б),в),г) Будут случайные события
Выразим их через элементарные события
Учитывая формулу вероятности произведения независимых случайных событий (наши элементарные события, очевидно, независимы)
находим соответствующие вероятности:
Здесь учтено, что
Задача 7. Надежность работы (вероятность безотказной работы) всех четырех узлов станка соответственно равны: 0,9; 0,8; 0,7; 0,6. Найти надежность работы станка. Найти вероятность, что при испытании N + 5 станков безотказную работу показали только N+2 станка.
Пример решения задачи 7. Надежность работы (вероятность безотказной работы) всех трех узлов устройства соответственно равны: 0,1; 0,2; 0,3. 1) Найти надежность работы устройства. 2) Найти вероятность, что при испытании 5 устройств безотказную работу показали только 3. Решение: Введем случайные события:
откуда
В соответствии с условием задачи, здесь предполагается, что узлы устройства работают независимо. Таким образом, вероятность безотказной работы всех трех узлов устройства (его надежность) представляется как произведения вероятностей безотказной работы всех устройств:
При испытании пяти одинаковых устройств
Таким образом, находим:
Задача 8. В результате социологических исследований получены следующие результаты: вероятность, что молодой специалист (неженатый или незамужняя), получивший высшее образование, два и более раз поменяет свое место работы в течение первого года после окончания вуза равно 0,1; вероятность, что поменяет один раз место работы – 0,3; вероятность, что не поменяет своего места работы – 0,6. Вероятность, что в течение первого года работы создаст семью – 0,7. Каков приблизительно количество молодых специалистов из 50N участников исследования в течение первого года работы (не)поменяют своего места работы и (не)создадут семьи. Заполнить таблицу.
Из числа 50N = …….. молодых специалистов
Пример решения задачи 8. В результате социологических исследований получены следующие результаты: вероятность, что молодой специалист (неженатый или незамужняя), получивший высшее образование, два раза поменяет свое место работы в течение первого года после окончания вуза равно 0,2; вероятность, что поменяет один раз место работы – 0,4; вероятность, что не поменяет своего места работы – 0,3. Вероятность, что в течение первого года работы создаст семью – 0,6. Каково, приблизительно, количество молодых специалистов из 1000 участников исследования в течение первого года работы (не) поменяют своего места работы и (не) создадут семьи. Заполнить таблицу. Решение: По смыслу вероятности случайного события, поменяют свое место работы 0,3 1000=300 человек; Один раз поменяют свое место работы 0,4 1000=400 человек; Два и более раз поменяют свое место работы 1000-300-400=300 человек.
Составим таблицу: Из 1000 молодых специалистов
Задача 9*. В результате статистических исследований в некотором городе X при опросе 50N молодых людей в возрасте от 20 до 25 лет выяснилось, что 70% человек являются студентами, из них 75% -это студенты вузов. 80% молодых людей, не являющихся студентами, тем не менее, обучаются в различных учебных заведениях. Найти вероятность, что из выбранных на удачу двух молодых людей а) первый окажется студентом, второй студентом вуза; б) первый где-то учится, второй – студент не вуза; в) один учится, другой не является студентом. Пример решения задачи 9*. В результате статистических исследований в некотором городе X при опросе 1000 молодых людей в возрасте от 16 до 24 лет выяснилось, что 80% человек являются студентами, из них 70% -это студенты вузов. 90% молодых людей, не являющихся студентами, тем не менее, обучаются в различных учебных заведениях. Найти вероятность, что из выбранных на удачу двух молодых людей а) первый окажется студентом, второй студентом вуза; б) первый где-то учится, второй – студент не вуза; в) один учится, другой не является студентом. Решение: Введем интересующие нас полную группу случайных событий (события, являются несовместными):
Соответствующие им противоположные события:
Тогда интересующими нас событиями для рассматриваемых случаев а),б),в) будут случайные события
которые можно представить в виде Дополнительные индексы, соответствуют номеру выбранного студента (первому или второму), кроме того, здесь мы различаем такие понятия, как «первый» и «один», «второй» и «другой» (см. условие примера). Выражение в круглых скобках представляет собой случайное событие – выбранный наудачу молодой человек, является студентом (в соответствии с определением суммы случайных событий). Считая результаты выбора первого и второго студента независимыми, и учитывая несовместность событий из полной группы событий, заданные в условии примера вероятности можно представить как
Здесь были использованы формула вероятности произведения независимых случайных событий
и формула суммы случайных событий
причем последняя формула, в случае несовместных событий, представлялась в упрощенном виде
Таким образом, искомые вероятности случайных событий окончательно могут быть вычислены:
Задача 10. Имеются две одинаковые урны Задачи 1. Из каждой урны вытягивается по одному шару. Найти вероятность, что вытянутые шары
а) одного цвета; б) разного цвета.
Пример решения задачи 10. Имеются две одинаковые корзины с фруктами Примера решения задачи 1. Из каждой корзины вытягивается по одному плоду. Найти вероятность, что вытянутые плоды а) одного вида; б) разного вида. Решение: Введем полную группу случайных событий (события несовместны):
тогда искомые случайные события
могут быть представлены в виде суммы несовместных событий
учитывая также, что результаты вытягивания плодов из разных корзин не зависят друг от друга, каждое из произведений составлено из несовместных событий, искомые вероятности можно представить в виде
Отметим, что сумма вероятностей равна единице, как и должно быть, с учетом того, что искомые случайные события образуют полную группу.
Задача 11. Между двумя участниками проводится игра «угадай мелодию». Участники по очереди угадывают одну мелодию. Участник А с первого раза угадывает мелодию с вероятностью N/(N+5), участник В с первого раза угадывает мелодию с вероятностьюN/(N + 8). С каждым последующим участием увеличивается вероятность угадывания на 0,1 для каждого игрока. Первым угадывать мелодию начинает участник А. Найти вероятности угадать мелодию каждым игроком при его трехкратном участии.
Пример решения задачи 11. Два баскетболиста поочередно бросают мяч в корзину до первого попадания, имея по три попытки. Вероятности попасть в корзину для первого игрока увеличиваются с каждым броском и имеет значения для первых трех бросков(0,6; 0,8; 0,9). Соответствующие вероятности для второго игрока -(0,6; 0,9; 0,95). Найти вероятности выигрыша обоими игроками. Решение: Введем элементарные случайные события:
Искомые случайные события
выражаем через элементарные события:
учитывая, что первый баскетболист может забить мяч в корзину и выиграть поединок при первом своем броске, при втором своем броске и при третьем своем броске. Аналогичная ситуация имеет место и для второго игрока. Черта над случайным событием означает промах соответствующего игрока при очередном броске. Поскольку все слагаемые являются несовместными случайными событиями, а все произведения имеют множителями независимые события, то формулы суммы вероятностей трех событий имеют упрощенный вид
как и формулы вероятности произведения случайных событий
откуда вероятности искомых событий могут быть представлены в виде
Отметим, что сумма вероятностей равна единице, как и должно быть, с учетом того, что искомые случайные события образуют полную группу.
|
||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2017-02-08; просмотров: 245; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.17.187.254 (0.01 с.) |

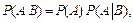
 условная вероятность события
условная вероятность события  при условии, что событие
при условии, что событие 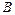 имело место.
имело место.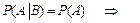

 предприятие №1 план выполнило;
предприятие №1 план выполнило; предприятие №2 план выполнило;
предприятие №2 план выполнило; предприятие №3 план выполнило.
предприятие №3 план выполнило.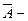 предприятие №1 план не выполнило;
предприятие №1 план не выполнило; предприятие №2 план не выполнило;
предприятие №2 план не выполнило; предприятие №3 план не выполнило.
предприятие №3 план не выполнило. ни одно предприятие не сорвало план;
ни одно предприятие не сорвало план; первое сорвало, второе нет;
первое сорвало, второе нет; первое сорвало, второе нет, третье сорвало;
первое сорвало, второе нет, третье сорвало; второе и третье сорвали план.
второе и третье сорвали план.
 .
. ,
,





 -й станок работает надежно. Тогда имеем равенство
-й станок работает надежно. Тогда имеем равенство ,
,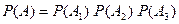 .
. .
.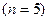 вероятность
вероятность  безотказной работы только трех станков
безотказной работы только трех станков  может быть найдена по формуле Бернулли
может быть найдена по формуле Бернулли
 .
. выбранный наудачу молодой человек нигде не учится;
выбранный наудачу молодой человек нигде не учится; выбранный молодой человек где-то учится;
выбранный молодой человек где-то учится; .
.
 ,
, ,
,
 .
. из первой корзины вытянуто яблоко;
из первой корзины вытянуто яблоко;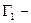 из первой корзины вытянута груша;
из первой корзины вытянута груша; из второй корзины вытянуто яблоко;
из второй корзины вытянуто яблоко; из второй корзины вытянута груша,
из второй корзины вытянута груша, вытянутые плоды разного вида
вытянутые плоды разного вида ;
;  ,
,
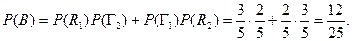
 второй игрок в i-ом броске попадает мячом в корзину.
второй игрок в i-ом броске попадает мячом в корзину. победил первый игрок;
победил первый игрок;  победил второй игрок
победил второй игрок ;
; ,
, ,
, ,
,
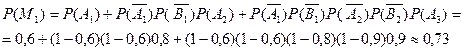 ;
;



