
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Вероятность случайных событийСодержание книги Поиск на нашем сайте
Определение вероятности
где
Задача 1. В урне находятся N шаров одинакового размера, причем m шаров белого цвета, остальные красные. Наудачу вытягивается n шаров. Найти вероятность, что среди вытянутых шаров будет k белых.
Пример решения задачи 1. В корзине три яблока и две груши. Найти вероятность, что из трех, вытянутых наудачу плодов, вытянутых яблок будет только два. Решение: Поскольку из пяти плодов вытягивается три плода, то этими плодами будут: два яблока и одна груша. Следовательно, вероятностью этого события будет величина
Здесь использовалось определение числа сочетаний из n по k:
Задача 2. В урну предыдущей задачи добавили еще 7 синих шаров. Найти вероятность, что среди вытянутых 12 шаров, будут 3 белых, 4 красных и 5 синих шаров.
Пример решения задачи 2. В корзину предыдущего примера добавили еще 5 лимонов. Найти вероятность, что из семи, вытянутых наудачу плодов будут вытянуты: две груши, одно яблоко и четыре лимона. Решение: Поскольку из десяти плодов вытягивается семь плодов, то общим числом исходов испытания будет
поскольку
Задача 3. Найти вероятность максимального выигрыша в спортлото N из 36, называя N номеров. (Из 36 видов спорта нужно угадать все N выигрышных).
Здесь и в дальнейшем N-номер варианта
Пример решения задачи 3. Найти вероятность максимального выигрыша в детском спортлото «тли из четылех».
Решение: Для максимального выигрыша ребенок должен угадать три правильных цифры из четырех возможных. Общее число всех возможностей выбрать три цифры из четырех, очевидно, есть число сочетаний из четырех по три
Задача 4. Найти вероятность минимального выигрыша в спортлото N (N>3, если N
Пример решения задачи 4. Найти вероятность минимального выигрыша в детском спортлото «тли из четылех», т.е. угадать только две правильные цифры. Решение: Для минимального выигрыша ребенок должен угадать только две правильных цифры из четырех возможных, выбирая три цифры. Общее число всех возможностей выбрать три цифры из четырех по-прежнему остается число сочетаний из четырех по три
Задача 5. Найти вероятность, вытягивая 4 карты из колоды 36 карт, вытянуть два валета, даму и короля. Ту же вероятность найти, вытягивая те же 4 карты из N колод.
Пример решения задачи 5. Найти вероятность, вытягивая 3 карты из колоды 52 карт, вытянуть тройку, семерку и туза. Ту же вероятность найти, вытягивая те же 3 карты из 5 колод. Решение: Аналогично предыдущему примеру, вытянуть три карты из 52-х можно
поскольку
В случае пяти колод аналогично получаем
поскольку
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2017-02-08; просмотров: 304; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.133.143.118 (0.007 с.) |

 случайного события
случайного события  :
: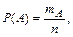


 ,
, общее число всех равновозможных исходов испытания,
общее число всех равновозможных исходов испытания, благоприятное для события
благоприятное для события 






 .
. . Благоприятным для искомого события числом испытаний будет произведение
. Благоприятным для искомого события числом испытаний будет произведение  , поскольку из двух груш вытягиваются две, из трех яблок вытягивается одно, а из пяти лимонов вытягиваться должно четыре. Таким образом, искомая вероятность интересующего нас события может быть найдена из определения вероятности как
, поскольку из двух груш вытягиваются две, из трех яблок вытягивается одно, а из пяти лимонов вытягиваться должно четыре. Таким образом, искомая вероятность интересующего нас события может быть найдена из определения вероятности как

 .
.

 Если номер варианта больше 10 (больше 20 и т.д.), то номер задачи соответствует номеру варианта минус 10 (или минус 20 для больших номеров и т.д.).
Если номер варианта больше 10 (больше 20 и т.д.), то номер задачи соответствует номеру варианта минус 10 (или минус 20 для больших номеров и т.д.).

 . А благоприятных искомому событию возможных сочетаний правильных цифр только одно (это выбор самих правильных цифр), то в соответствии с определением вероятности случайного события, окончательно получаем
. А благоприятных искомому событию возможных сочетаний правильных цифр только одно (это выбор самих правильных цифр), то в соответствии с определением вероятности случайного события, окончательно получаем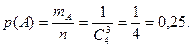
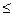 3, то заменить N
3, то заменить N  N+3) из 36, называя N номеров, т.е. угадать только три выигрышных вида спорта (если N>3, если же N
N+3) из 36, называя N номеров, т.е. угадать только три выигрышных вида спорта (если N>3, если же N 
 числом способов (общее число всех равновозможных исходов испытания
числом способов (общее число всех равновозможных исходов испытания 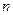 ). Благоприятные исходы испытания заключаются в вытягивании одной тройки из четырех (по количеству мастей), одной семерки их четырех и одного туза из четырех. Таким образом, в соответствии с определением вероятности случайного события, окончательно имеем
). Благоприятные исходы испытания заключаются в вытягивании одной тройки из четырех (по количеству мастей), одной семерки их четырех и одного туза из четырех. Таким образом, в соответствии с определением вероятности случайного события, окончательно имеем


 .
.


