
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Непосредственный подсчет вероятностейСодержание книги Похожие статьи вашей тематики
Поиск на нашем сайте
Теория вероятностей Программа Методические указания к изучению курса по теории вероятностей (для студентов заочной формы обучения)
Специальность 230101 – вычислительные машины, комплексы, системы и сети Направление 654600 – информатика и вычислительная техника
Издательство Иркутского государственного технического университета
Теория вероятностей: метод.указания /сост.: Виктор Григорьевич Кирий, Иркутск: Изд-во ИрГТУ, 2011, 36с.
Соответствует содержанию разделов государственного образовательного стандарта по направлению 654600 «Информатика и вычислительная техника». Изложены программа, краткие теоретические сведения и список задач по теории вероятностей, примеры их решения. Предназначены для студентов – заочников по специальности 230101 «Вычислительные машины, комплексы, системы и сети», факультета кибернетики.
Табл. 4 Библиогр.:4
Рецензент: кандидат технических наук, доцент С.В.Бахвалов
Оглавление
1. Программа ………………………………………………………………. 4 2. Краткие теоретические сведения по основным разделам теории вероятностей…………………………………………………………………. 5 2.1.Основные понятия и определения……………………………………. 5 2.2.Основные теоремы теории вероятностей о событиях……………….. 6 2.3.Случайные величины и их законы распределения…………………… 9 2.4.Системы случайных величин…………………………………………...17 2.5.Числовые характеристики функций случайных величин…………….20 2.6.Случайные функции……………………………………………………..22 3. Предельные теоремы теории вероятностей …………………………...24 3.1.Неравенство Чебышева………………………………………………… 24 3.2.Закон больших чисел (теорема Чебышева)…………………………... 24 3.3.Закон больших чисел в форме теоремы Маркова…………………. 25 3.4.Следствия закона больших чисел (теорема Бернулли и Пуассона).. 25 3.5.Центральная предельная теорема…………………………………… 26 4. Список задач по теории вероятностей, используемых на занятиях по этой дисциплине …………………………………………………………….. 27 5. Примеры решения некоторых задач по теории вероятностей ………29 6. Экзаменационные билеты и контрольные задания……………………………………………………………………………… 33 7.Список литературы… ……………………………………………………..36
ПРОГРАММА 1. Предмет теории вероятностей. Комплекс условий. Классическое определение вероятности. Cтатистическая вероятность. 2. События и их виды. Полная группа событий. Операции над событиями. 3. Геометрические вероятности. 4. Теорема сложения вероятностей и ее следствия. 5. Теорема умножения вероятностей и ее следствия. 6. Формула полной вероятности. 7. Формула Байеса. 8. Независимые испытания. Схема Бернулли. 9. Биномиальное распределение вероятностей. 10. Теорема Пуассона и ее применения. 11. Случайные величины. Основные определения. 12. Функция распределения и ее свойства. 13. Плотность распределения вероятностей и ее свойства. 14. Числовые характеристики случайных величин. Классификация. Математическое ожидание. 15. Вероятность попадания случайной величины на заданный участок. 16. Характеристики положения (начальные моменты, мода, медиана). 17. Характеристики формы (центральные моменты, дисперсия). 18. Коэффициенты асимметрии и эксцесса. 19. Экспоненциальный закон распределения вероятностей. 20. Равномерный закон распределения вероятностей. 21. Нормальный закон распределения вероятностей. 22. Параметры нормального закона распределения вероятностей. Правило «трех сигм». 23. Системы случайных величин. Функция распределения системы двух случайных величин, ее свойства. 24. Функция нормального закона распределения, интеграл вероятности. 25. Плотность распределения вероятностей системы двух случайных величин и ее свойства. 26. Закон распределения вероятностей отдельных величин, входящих в систему. 27. Условный закон распределения вероятностей случайных величин, входящих в систему. 28. Числовые характеристики системы двух случайных величин. Корреляционный момент и коэффициент корреляции. 29. Функции случайных величин. Свойства математического ожидания и дисперсии. 30. Закон больших чисел. 31. Неравенство Чебышева. 32. Закон больших чисел в форме теоремы Чебышева и теоремы Маркова. 33. Следствия закона больших чисел: теоремы Я. Бернулли и Пуассона. 34. Центральная предельная теорема. 2.Краткие теоретические сведения по основным разделам теории вероятностей.
2.1.Основные понятия и определения.
Событие – всякий факт, который в результате опыта может произойти или не произойти. Вероятность события – численная мера степени объективной возможности того, что событие может произойти. В теории вероятностей в качестве единицы измерения степени возможности появления события принята вероятность достоверного события, т.е. такого события, которое в результате опыта непременно произойдет. Вероятность такого события равна единице, а вероятность противоположного события, которое называется невозможным, равна нулю. Отсюда следует, что вероятность любого другого события изменяется в пределах от нуля до единицы. Полная группа событий – несколько событий в данном опыте образуют полную группу событий, если в результате опыта непременно должно появиться, хотя бы одно из них. Несовместные события – несколько событий называются несовместными в данном опыте, если никакие два из них не могут появиться вместе. Противоположными событиями называются два несовместных события, образующих полную группу. Равновозможные события - несколько событий в данном опыте называются равновозможными, если по условиям симметрии есть основание считать, что ни одно из этих событий не является объективно более возможным, чем другое. Случаи – события, образующие группу, обладающую всеми тремя свойствами, называются случаями. Благоприятный случай – случай, называется благоприятным некоторому событию, если появление этого случая влечет за собой появление данного события.
Статистическая вероятность Если произведена серия из n опытов, в каждом из которых могло появиться некоторое событие А, то статистической вероятностью называется отношение числа опытов, в которых появилось событие А, к общему числу произведенных опытов:
где m – число появлений события А; n – общее число произведенных опытов. Характерной особенностью статистической вероятности, в отличие от классической, является то, что она является случайной величиной, значение которой зависит от числа произведенных опытов. Однако при увеличении числа опытов частота события все более теряет свой случайный характер и приближается к некоторой постоянной величине.
Геометрическая вероятность Если в результате опыта число исходов имеет мощность континиумма, т.е. их число бесконечное множество, тогда вероятность события определяется как отношение меры множества благоприятствующих исходов к мере множества всех исходов:
где s -,например, площадь множества благоприятствующих исходов, S – общая площадь всех исходов опыта. Заметим, что геометрическая вероятность – тоже постоянная величина и может быть вычислена до проведения опыта.
Формула полной вероятности. Требуется определить вероятность некоторого события А, которое может произойти вместе с одним из событий
Теорема гипотез (формула Бейеса). Имеется полная группа несовместных гипотез
Закон равномерной плотности Относится к непрерывным случайным величинам, о которых заранее известно, что их возможные значения лежат в пределах некоторого определенного интервала; кроме того, известно, что в пределах этого интервала все значения случайной величины одинаково вероятны (точнее, обладают одной и той же плотностью вероятности). Для случайной величины Х, подчиненной закону равномерной плотности на участке от α до
Функция распределения имеет вид: 0 при
1 при
Математическое ожидание величины Х равно:
В силу симметричности равномерного распределения медиана величины Х также равна
Моды закон равномерной плотности не имеет. Дисперсия равномерной величины равна:
Откуда среднеквадратическое отклонение равно:
В силу симметричности распределения его асимметрия равна нулю:
Эксцесс равен:
Определяем среднее арифметическое отклонение:
Вычислим вероятность попадания случайной величины Х, распределенной по закону равномерной плотности, на участок (а,б), представляющий собой часть участка (
Системы случайных величин Если результат опыта описывается не одной случайной величиной, а двумя или более случайными величинами, то имеем дело с системой случайных величин. Условимся систему нескольких случайных величин Х, У,..., W обозначать (Х, У,..., W). Свойства системы нескольких случайных величин не исчерпываются свойствами отдельных величин, ее составляющих; помимо этого они включают также взаимные связи (зависимости) между случайными величинами. Законы распределения системы случайных величин. Функцией распределения системы двух случайных величин (Х, У) называется вероятность совместного выполнения двух неравенств X<x и Y<y:
Функция распределения 1. при при 2. Повсюду на - ∞ функция распределения равна нулю:
3. При одном из аргументов, равном + ∞, функция распределения системы превращается в функцию распределения случайной величины, соответствующей другому аргументу:
где 4. Если оба аргумента равны + ∞, функция распределения системы равна единице:
Через функцию распределения легко решается задача вычисления вероятности попадания случайной точки в заданную область, когда эта область представляет собой прямоугольник со сторонами параллельными координатным осям:
Где Плотностью распределения системы двух случайных величин называется функция, которая представляет собой вторую смешанную частную производную функции
Для плотности вероятности системы вводится понятие «элемента вероятности», который показывает вероятность попадания случайной точки в элементарный прямоугольник со сторонами
Пользуясь понятием элемента вероятности, легко решается задача вычисления вероятности попадания случайной точки в произвольную область D:
Из этой формулы вытекает формула для вероятности попадания в прямоугольник R, ограниченный абсциссами
Воспользуемся этой формулой для того, чтобы выразить функцию распределения системы двух случайных величин через плотность распределения:
Плотность распределения обладает следующими двумя свойствами: 1. Плотность распределения системы есть функция неотрицательная: 2. Двойной интеграл в бесконечных пределах от плотности распределения системы равен единице:
Законы распределения отдельных случайных величин, входящих в систему. Условные законы распределения. Зная закон распределения системы двух случайных величин, можно всегда определить законы распределения отдельных случайных величин, входящих в систему. Воспользовавшись третьим свойством функции распределения и интегральной связью между функцией распределения и плотностью распределения, напишем
Откуда, дифференцируя по х, получим выражение для плотности распределения величины Х
Аналогично
Приведенные формулы дают возможность, зная закон распределения системы, найти законы распределения отдельных величин, входящих в систему. Естественно, возникает вопрос об обратной задаче: нельзя ли по законам распределения отдельных величин, входящих в систему, восстановить закон распределения системы? Оказывается, что в общем случае сделать этого нельзя, так как для этого нужно еще знать зависимость между величинами, входящими в систему. Эта зависимость характеризуется с помощью, так называемых условных законов распределения. Условным законом распределения величины Х, входящей в систему (Х,У), называется ее закон распределения, вычисленный при условии, что другая случайная величина У приняла определенное значение у. Условная функция распределения обозначается Зная закон распределения одной из величин, входящих в систему, и условный закон распределения второй, можно составить закон распределения системы. Вывод формулы опирается на использование теоремы умножения вероятностей для зависимых событий:
Эту формулу часто называют теоремой умножения законов распределения. Аналогично можно написать:
Разрешая эти формулы относительно условных законов распределения, получаем:
или
Случайные функции Основные понятия и определения Случайные величины, изменяющиеся в процессе опыта, мы будем в отличие от обычных случайных величин называть случайными функциями. Случайной функцией называется функция, которая в результате опыта может принять тот или иной конкретный вид, неизвестно заранее – какой именно. Конкретный вид, принимаемый случайной функцией в результате опыта, называется реализацией случайной функции. Если над случайной функцией произвести группу опытов, то мы получим множество реализаций. Случайные функции будем обозначать большими буквами Чисто теоретически закон распределения случайной функции представляет собой функцию бесчисленного множества аргументов, практическое использование которой совершенно исключено. В связи с этим вводят в рассмотрение частные случаи законов распределения случайной функции. Одномерный закон распределения вероятностей Двумерный закон распределения вероятностей Трехмерный закон распределения вероятностей Очевидно, что можно неограниченно увеличивать число аргументов и получать при этом более подробную информацию о характеристиках случайной функции, но оперировать со столь громоздкими функциями крайне неудобно. Примеры решения некоторых задач по теории вероятностей 5.1.Непосредственный подсчет вероятностей. В партии из Решение. Число возможных способов взять
5.2. Геометрические вероятности. В любые моменты промежутка времени Решение. Пусть Областью возможных значений
5.3. Теорема умножения вероятностей. Определить вероятность того, что выбранное наудачу изделие является первосортным, если известно, что 4% всей продукции являются браком, а 75% не бракованных изделий удовлетворяют требованиям первого сорта. Решение. Пусть событие А состоит в том, что выбранное изделие не бракованное, а событие В – выбранное изделие первосортное. Тогда вероятность Р(А) = 1-0,04 = 0,96, а условная вероятность Р(В/А) = 0,75. Искомая вероятность равна вероятности произведения двух событий АВ: 5.4. Теорема сложения вероятностей. Ведется стрельба по самолету, уязвимыми агрегатами которого являются два двигателя и кабина пилота. Для того, чтобы поразить самолет, достаточно поразить оба двигателя вместе или кабину пилота. Вероятность поражения первого двигателя равна Решение. Событие А – поражение самолета есть сумма двух совместных событий: Д – поражение обоих двигателей и К – поражение кабины. Следовательно, Р(А) = Р(Д)+Р(К)-Р(ДК) = 5.5. Формула полной вероятности. Прибор может работать в двух режимах: нормальном и не нормальном. Нормальный режим наблюдается в 80% всех случаев работы прибора, а не нормальный – в 20%. Вероятность выхода прибора из строя в нормальном режиме равна 0,1, а в не нормальном – 0,7. Найти полную вероятность выхода прибора из строя. Решение. В соответствии с формулой полной вероятности искомая вероятность равна 5.6. Формула Байеса. В группе из 10 студентов, пришедших на экзамен, 3 отличника, 4 хорошиста, 2 троечника и 1 двоечник. В экзаменационных билетах имеется 20 вопросов. Отличник может ответить на все вопросы, хорошо подготовленный может ответить на 16 вопросов, троечник – на10, двоечник – на 5. Вызванный наугад студент ответил на три произвольно заданных вопроса. Найти вероятность того, что этот студент отличник. Решение. Выдвигаем четыре гипотезы:
Для сравнения вычислим вероятность, что отвечавший студент был двоечник:
Формула Бернулли Что вероятнее, выиграть у равносильного противника: три партии из четырех или пять из восьми? Решение. Так как противники равные, то вероятность выигрыша у них равна 0,5. Применяя, формулу Бернулли имеем:
т.е. Закон Пуассона Радиоаппаратура состоит из 1000 электроэлементов. Вероятность отказа одного элемента в течение одного года работы равна 0,001 и не зависит от состояния других элементов. Какова вероятность отказа двух и не менее двух электроэлементов за год? Решение. Считая случайное число Х отказавших элементов подчиняющимся закону Пуассона с параметром 1) вероятность отказа ровно двух элементов
2) вероятность отказа не менее двух элементов, вычисляется через противоположное событие
Показательный закон Электронная лампа работает исправно в течение случайного времени Т, распределенного по показательному закону Решение. Отказы ламп образуют простейший поток событий с плотностью а) в) Равномерный закон На перекрестке стоит автоматический светофор, в котором 1 минуту горит зеленый свет и 0,5 минуты – красный, затем опять 1 минуту горит зеленый свет, 0,5 минуту – красный и т.д. Некто подъезжает к перекрестку на машине в случайный момент, не связанный с работой светофора. Найти вероятность того, что он проедет перекресток, не останавливаясь. Решение. Момент проезда автомашины через перекресток распределен равномерно в интервале, равном периоду смены цветов в светофоре. Этот период равнее 1+0,5=1,5 минут. Для того, чтобы машина проехала через перекресток не останавливаясь, достаточно, чтобы момент проезда перекрестка пришелся на интервал времени (0;1). Для равномерно распределенной случайной величины в интервале (0;1,5) вероятность попасть в интервал (0;1) равна 2/3. Система случайных величин Имеются две независимые случайные величины (Х,У), подчиненные каждая показательному закону:
Написать выражение для плотности распределения системы и найти функцию распределения системы (Х,У). Решение. Так как случайные величины независимые, то искомые функции равны произведению соответствующих функций каждой случайной величины:
Случайные функции Случайная функция Х( Решение. Используя теоремы о числовых характеристиках, получаем, что Случайная функция Х( Закон больших чисел Пример 1. Вероятность появления события А в одном опыте равна 0,5. Можно ли с вероятностью, большей 0,97, утверждать, что число появлений события А в 1000 независимых опытах будет в пределах от 400 до 600? Решение. Число появлений события А является случайной величиной, которая имеет математическое ожидание равное
Ответ на вопрос, поставленный в задаче положительный. Пример 2. Определить, имеет ли место закон больших чисел для среднего арифметического из n попарно независимых случайных величин
Решение. Согласно закону больших чисел в форме теоремы Чебышева необходимо определить имеют ли независимые случайные величины Так как дисперсия Другие примеры решения задач по теории вероятностей приведены в задачнике Е.С. Вентцель, Л.А.Овчаров «Теория вероятностей», изд-во «Наука», М.:1973г, а также в «Сборнике задач по теории вероятностей, математической статистике и теории случайных функций» под редакцией А.А. Свешникова, «Наука», М.:1970г. Билеты для экзамена Билет №1 1. Основные понятия теории вероятности. 2. Центральная предельная теорема. 3. Задача 30.3 (а). Билет №2 1. Классическая, частотная, геометрическая схема вычисления вероятности. 2. Неравенство Чебышева. 3. Задача 30.3. (б) Билет №3 1. Теорема сложения вероятностей. 2. Полиномиальное распределение вероятностей. 3. Задача 30.3 (в). Билет №4 1. Теорема умножения вероятностей. 2. Два примера применения центральной предельной теоремы. 3. Задача 29.6 Билет №5 1. Независимые и зависимые события. 2. Следствия закона больших чисел. 3. Задача 29.9 (а). Билет №6 1. Формула полной вероятности. 2. Понятие об усиленном законе больших чисел. 3. Задача 15.3. Билет №7 1. Формула Байеса. 2. Закон больших чисел для зависимых случайных величин. 3. Задача 15.4. Билет №8 1. Схема независимых испытаний. Биномиальное распределение. 2. Теорема Пуассона, как одна из форм закона больших чисел. 3. 3.Задача 13.9. Билет №9 1. Обобщение схемы независимых испытаний. Локальная теорема Муавра – Лапласа. 2. Теорема Бернулли, как одна из форм закона больших чисел. 3. Задача 13.1 (а,б). Билет №10 1. Функции распределения случайных величин. 2. Закон больших чисел в форме теоремы Чебышева. 3. Задача 10.3. Билет №11 1. Плотность распределения случайных величин. 2. Неравенство Чебышева. 3. 3.Задача 12.3. Билет №12 1. Числовые характеристики случайных величин. Характеристики положения. 2. Закон больших чисел. 3. Задача 12.10. Билет №13 1. Числовые характеристики случайных величин. Моменты. Дисперсия. 2. Понятие о стационарных случайных функциях в широком смысле. 3. Задача 10.5. Билет №14 1. Биномиальный ЗРВ случайных величин, его числовые характеристики. 2. Корреляционная функция случайных функций, ее свойства. Взаимная корреляционная функция. 3. Задача 8.4 Билет №15 1. Распределение Пуассона, его числовые характеристики. 2. Характеристики случайных функций: 3. 3.Задача 8.6. Билет №16 1. Равномерное распределение, его характеристики. 2. Понятие случайной функции. Закон распределения случайной функции, плотность распределения случайной функции. 3. Задача 8.9. Билет №17 1. Показательное (экспоненциальное) распределение, его числовые характеристики. 2. Теоремы о числовых характеристиках: 3. 3.Задача 7.3. <
|
||||||||||||
|
Последнее изменение этой страницы: 2017-02-08; просмотров: 685; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 13.58.61.176 (0.021 с.) |

 ,
,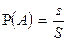 ,
,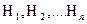 , образующих полную группу событий, называемых в теории вероятностей гипотезами. Эта вероятность вычисляется с помощью формулы полной вероятности:
, образующих полную группу событий, называемых в теории вероятностей гипотезами. Эта вероятность вычисляется с помощью формулы полной вероятности: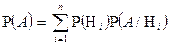 .
.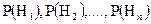 . Произведен опыт, в результате которого наблюдено появление некоторого события А. Спрашивается, как следует изменить вероятности гипотез в связи с появлением этого события? Здесь, по существу, речь идет о том, чтобы найти условную вероятность
. Произведен опыт, в результате которого наблюдено появление некоторого события А. Спрашивается, как следует изменить вероятности гипотез в связи с появлением этого события? Здесь, по существу, речь идет о том, чтобы найти условную вероятность 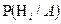 для каждой гипотезы. Эта вероятность ищется по формуле Бейеса:
для каждой гипотезы. Эта вероятность ищется по формуле Бейеса:
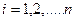 .
.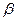 , плотность вероятности постоянна и имеет вид:
, плотность вероятности постоянна и имеет вид: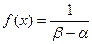 при
при 
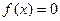 при
при 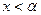 или
или  .
.
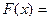
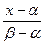 при
при 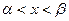
 .
. =
= 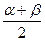 .
.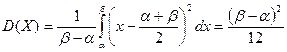 ,
,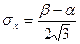 .
.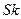 =0.
=0.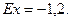
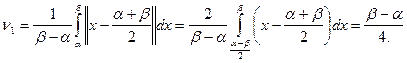 .
.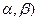 :
: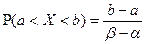 .
. .
.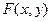 обладает следующими свойствами:
обладает следующими свойствами: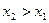
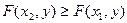 ;
;
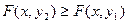 .
.
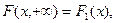

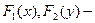 соответственно функции распределения случайных величин Х и У.
соответственно функции распределения случайных величин Х и У.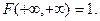
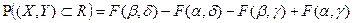
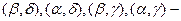 координаты вершин четырех бесконечных квадранта на плоскости х0у.
координаты вершин четырех бесконечных квадранта на плоскости х0у.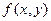

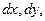 примыкающий к точке (х,у)
примыкающий к точке (х,у)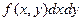
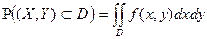 .
.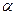 и
и  и
и 
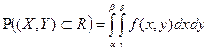
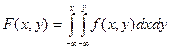
 .
.



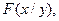 условная плотность распределения
условная плотность распределения 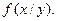
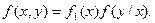
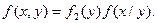
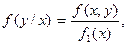
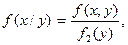

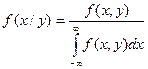
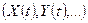 . При фиксированном значении аргумента t случайная функция превращается в обычную случайную величину.
. При фиксированном значении аргумента t случайная функция превращается в обычную случайную величину.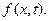
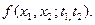
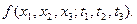
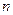 изделий
изделий 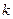 бракованных. Определить вероятность того, что среди выбранных наудачу для проверки
бракованных. Определить вероятность того, что среди выбранных наудачу для проверки 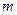 изделий ровно
изделий ровно 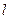 окажутся бракованными.
окажутся бракованными.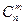 . Благоприятствующими являются случаи, когда из общего числа
. Благоприятствующими являются случаи, когда из общего числа  способами), а остальные
способами), а остальные 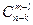 способами. Поэтому число благоприятствующих случаев равно
способами. Поэтому число благоприятствующих случаев равно 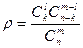 .
. равновозможны поступления в приемник двух сигналов. Приемник будет забит, если разность между моментами поступления сигналов будет меньше
равновозможны поступления в приемник двух сигналов. Приемник будет забит, если разность между моментами поступления сигналов будет меньше 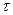 . Определить вероятность того, что приемник будет забит.
. Определить вероятность того, что приемник будет забит.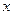 и
и  - моменты поступления сигналов в приемник.
- моменты поступления сигналов в приемник.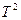 . Приемник будет забит, если
. Приемник будет забит, если  . Данная область лежит между прямыми
. Данная область лежит между прямыми 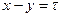 и
и 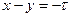 . Ее площадь равна
. Ее площадь равна  , поэтому искомая вероятность равна
, поэтому искомая вероятность равна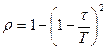 .
.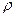 =Р(АВ) = 0,96×0,75 = 0,72.
=Р(АВ) = 0,96×0,75 = 0,72.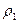 , второго двигателя
, второго двигателя 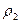 , кабины пилота
, кабины пилота 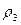 . Найти вероятность того, что самолет будет поражен.
. Найти вероятность того, что самолет будет поражен.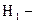 студент отличник;
студент отличник; 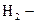 студент хорошист;
студент хорошист;  студент троечник;
студент троечник; 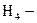 студент двоечник. До опыта:
студент двоечник. До опыта: 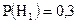 ;
;  ;
; 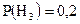 ;
;  . Событие А – это то, что вызванный студент ответил на три вопроса. Условная вероятность этого события равна
. Событие А – это то, что вызванный студент ответил на три вопроса. Условная вероятность этого события равна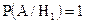 ;
; 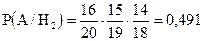 ;
;  ;
; 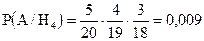 . После опыта, применяя формулу Байеса, имеем:
. После опыта, применяя формулу Байеса, имеем: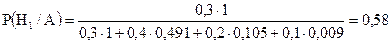 .
.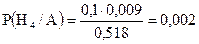 .
. ;
;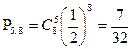 ;
;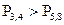 .
.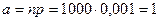 , получим:
, получим: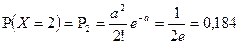 ;
;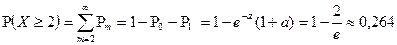 .
.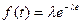 при
при 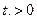 и равна 0 при
и равна 0 при 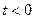 . По истечении времени Т лампа выходит из строя, после чего ее немедленно заменяют новой. Найти вероятность того, что за время
. По истечении времени Т лампа выходит из строя, после чего ее немедленно заменяют новой. Найти вероятность того, что за время  . Математическое ожидание числа отказов за время
. Математическое ожидание числа отказов за время 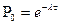 ; б)
; б) 
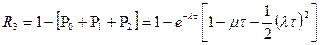 .
.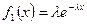 при х>0, и равна 0 при х<0;
при х>0, и равна 0 при х<0; 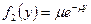 при у>0, и равна 0 при у<0.
при у>0, и равна 0 при у<0. при х>0 и у>0;
при х>0 и у>0; 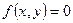 при х<0 или у<0.
при х<0 или у<0.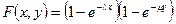 при х>0 и у>0;
при х>0 и у>0; 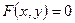 при х
при х  или у
или у  задана выражением
задана выражением 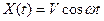 , где V – случайная величина с характеристиками
, где V – случайная величина с характеристиками  ;
;  . Найти характеристики случайной функции
. Найти характеристики случайной функции 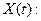
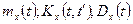 . Определить, является ли случайная функция Х(
. Определить, является ли случайная функция Х(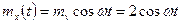 ;
; 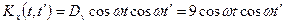 ;
; 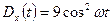 .
.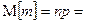 500 и дисперсию, равную
500 и дисперсию, равную  250. Следовательно величина отклонения числа появления события А в 1000 опытах от математического ожидания
250. Следовательно величина отклонения числа появления события А в 1000 опытах от математического ожидания 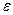 равна 100. Для оценки вероятности того, что величина такого отклонения по абсолютной величине не превзойдет 100, применим неравенство Чебышева, с той особенностью, что перейдем к противоположному событию
равна 100. Для оценки вероятности того, что величина такого отклонения по абсолютной величине не превзойдет 100, применим неравенство Чебышева, с той особенностью, что перейдем к противоположному событию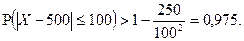
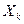 , заданных рядом распределения
, заданных рядом распределения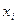

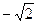
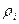
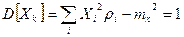 , так как
, так как 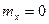 .
.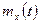 ,
, 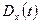

 ,
, 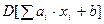 ,
, 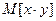 ,
, 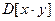 .
.


