
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Следствия закона больших чисел: теоремы Бернулли и Пуассона
Теорема Бернулли утверждает, что при неограниченном увеличении числа опытов n частота события А сходится по вероятности к его вероятности p
где Большое значение этой теоремы в том, что по статистической вероятности можно с большой долей вероятности оценивать классическую вероятность. Теорема Пуассона утверждает, что если производится n независимых опытов и вероятность появления события А в i- м опыте равна
3.5. Центральная предельная теорема для одинаково распределенных случайных величин. Если При определенных условиях эта теорема справедлива и для неодинаково распределенных слагаемых. Например, в качестве таких условий можно привести условия А.М.Ляпунова:
где
Наиболее общим (необходимым и достаточным) условием справедливости центральной предельной теоремы является условие Линдеберга: при любом
где Список задач по теории вероятностей, используемых на занятиях по этой дисциплине.
Примеры решения некоторых задач по теории вероятностей 5.1.Непосредственный подсчет вероятностей. В партии из Решение. Число возможных способов взять
5.2. Геометрические вероятности. В любые моменты промежутка времени Решение. Пусть Областью возможных значений
5.3. Теорема умножения вероятностей. Определить вероятность того, что выбранное наудачу изделие является первосортным, если известно, что 4% всей продукции являются браком, а 75% не бракованных изделий удовлетворяют требованиям первого сорта. Решение. Пусть событие А состоит в том, что выбранное изделие не бракованное, а событие В – выбранное изделие первосортное. Тогда вероятность Р(А) = 1-0,04 = 0,96, а условная вероятность Р(В/А) = 0,75. Искомая вероятность равна вероятности произведения двух событий АВ: 5.4. Теорема сложения вероятностей. Ведется стрельба по самолету, уязвимыми агрегатами которого являются два двигателя и кабина пилота. Для того, чтобы поразить самолет, достаточно поразить оба двигателя вместе или кабину пилота. Вероятность поражения первого двигателя равна
Решение. Событие А – поражение самолета есть сумма двух совместных событий: Д – поражение обоих двигателей и К – поражение кабины. Следовательно, Р(А) = Р(Д)+Р(К)-Р(ДК) = 5.5. Формула полной вероятности. Прибор может работать в двух режимах: нормальном и не нормальном. Нормальный режим наблюдается в 80% всех случаев работы прибора, а не нормальный – в 20%. Вероятность выхода прибора из строя в нормальном режиме равна 0,1, а в не нормальном – 0,7. Найти полную вероятность выхода прибора из строя. Решение. В соответствии с формулой полной вероятности искомая вероятность равна 5.6. Формула Байеса. В группе из 10 студентов, пришедших на экзамен, 3 отличника, 4 хорошиста, 2 троечника и 1 двоечник. В экзаменационных билетах имеется 20 вопросов. Отличник может ответить на все вопросы, хорошо подготовленный может ответить на 16 вопросов, троечник – на10, двоечник – на 5. Вызванный наугад студент ответил на три произвольно заданных вопроса. Найти вероятность того, что этот студент отличник. Решение. Выдвигаем четыре гипотезы:
Для сравнения вычислим вероятность, что отвечавший студент был двоечник:
Формула Бернулли Что вероятнее, выиграть у равносильного противника: три партии из четырех или пять из восьми? Решение. Так как противники равные, то вероятность выигрыша у них равна 0,5. Применяя, формулу Бернулли имеем:
т.е.
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2017-02-08; просмотров: 729; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.191.228.88 (0.009 с.) |
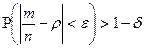 ,
,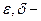 сколь угодно малые положительные числа.
сколь угодно малые положительные числа.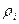 , то при увеличении n частота события А сходится по вероятности к среднему арифметическому вероятностей
, то при увеличении n частота события А сходится по вероятности к среднему арифметическому вероятностей  .
.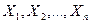 , … независимые случайные величины, имеющие один и тот же закон распределения с математическим ожиданием
, … независимые случайные величины, имеющие один и тот же закон распределения с математическим ожиданием 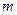 и дисперсией
и дисперсией  , то при неограниченном увеличении n закон распределения суммы
, то при неограниченном увеличении n закон распределения суммы  неограниченно приближается к нормальному закону распределения.
неограниченно приближается к нормальному закону распределения.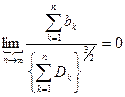 ,
,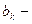 третий абсолютный центральный момент величины
третий абсолютный центральный момент величины 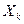 :
: .
.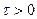

 математическое ожидание,
математическое ожидание, 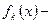 плотность распределения случайной величины
плотность распределения случайной величины 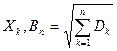 .
.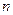 изделий
изделий 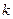 бракованных. Определить вероятность того, что среди выбранных наудачу для проверки
бракованных. Определить вероятность того, что среди выбранных наудачу для проверки 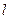 окажутся бракованными.
окажутся бракованными.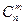 . Благоприятствующими являются случаи, когда из общего числа
. Благоприятствующими являются случаи, когда из общего числа  способами), а остальные
способами), а остальные 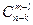 способами. Поэтому число благоприятствующих случаев равно
способами. Поэтому число благоприятствующих случаев равно 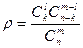 .
. равновозможны поступления в приемник двух сигналов. Приемник будет забит, если разность между моментами поступления сигналов будет меньше
равновозможны поступления в приемник двух сигналов. Приемник будет забит, если разность между моментами поступления сигналов будет меньше 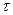 . Определить вероятность того, что приемник будет забит.
. Определить вероятность того, что приемник будет забит.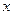 и
и  - моменты поступления сигналов в приемник.
- моменты поступления сигналов в приемник.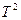 . Приемник будет забит, если
. Приемник будет забит, если  . Данная область лежит между прямыми
. Данная область лежит между прямыми 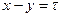 и
и 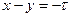 . Ее площадь равна
. Ее площадь равна  , поэтому искомая вероятность равна
, поэтому искомая вероятность равна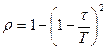 .
.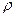 =Р(АВ) = 0,96×0,75 = 0,72.
=Р(АВ) = 0,96×0,75 = 0,72.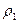 , второго двигателя
, второго двигателя 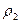 , кабины пилота
, кабины пилота 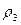 . Найти вероятность того, что самолет будет поражен.
. Найти вероятность того, что самолет будет поражен.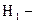 студент отличник;
студент отличник; 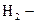 студент хорошист;
студент хорошист;  студент троечник;
студент троечник; 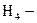 студент двоечник. До опыта:
студент двоечник. До опыта: 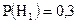 ;
;  ;
; 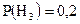 ;
;  . Событие А – это то, что вызванный студент ответил на три вопроса. Условная вероятность этого события равна
. Событие А – это то, что вызванный студент ответил на три вопроса. Условная вероятность этого события равна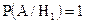 ;
; 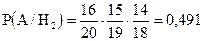 ;
;  ;
; 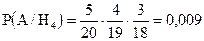 . После опыта, применяя формулу Байеса, имеем:
. После опыта, применяя формулу Байеса, имеем: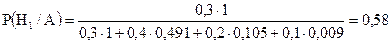 .
.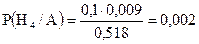 .
. ;
;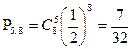 ;
;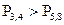 .
.


