Основные теоремы теории вероятностей о событиях

Сумма и произведение событий.

Суммой двух событий А и В называется событие С, состоящее в выполнении события А или события В, или обоих вместе. Обозначается как С = А+В.

Если события А и В несовместны, то естественно, что появление обоих этих событий вместе отпадает, и сумма событий сводится к появлению или события А, или события В.

Суммой нескольких событий называется событие, состоящее в появлении хотя бы одного из этих событий.

Произведением двух событий А и В называется событие С, состоящее в совместном выполнении события А и события В. Обозначается как С = АВ. Если события А и В несовместные, то их произведение является невозможным событием.

Произведением нескольких событий называется событие, состоящее в совместном появлении всех этих событий.

 

Теорема сложения вероятностей.

Вероятность суммы двух несовместных событий равна сумме вероятностей этих событий:

.

Следствие 1. Если события образуют полную группу несовместных событий, то сумма их вероятностей равна единице.

Следствие 2.Сумма вероятностей противоположных событий равна единице.

Для двух совместных событий вероятность суммы этих событий выражается формулой

.

 

Теорема умножения вероятностей.

Событие А называется независимым от события В, если вероятность события А не зависит от того, произошло событие В или нет.

Событие А называется зависимым от события В, если вероятность события А меняется в зависимости от того, произошло событие В или нет.

Вероятность события А, вычисленная при условии, что имело место другое событие В, называется условной вероятностью события А и обозначается

.

Условие независимости события А от события В можно записать в виде:

= .

Теорема умножения вероятностей формулируется следующим образом.

Вероятность произведения двух событий равна произведению вероятности одного из них на условную вероятность другого, вычисленную при условии, что первое имело место:

Следствие1. Если событие А не зависит от события В, то и событие В не зависит от события А.

Следствие 2. Вероятность произведения двух независимых событий равна произведению вероятностей этих событий:

.

 

Формула полной вероятности.

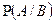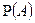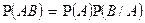
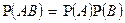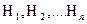Требуется определить вероятность некоторого события А, которое может произойти вместе с одним из событий , образующих полную группу событий, называемых в теории вероятностей гипотезами. Эта вероятность вычисляется с помощью формулы полной вероятности:

.

Теорема гипотез (формула Бейеса).

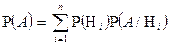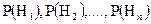Имеется полная группа несовместных гипотез . Вероятности этих гипотез до опыта известны и равны соответственно . Произведен опыт, в результате которого наблюдено появление некоторого события А. Спрашивается, как следует изменить вероятности гипотез в связи с появлением этого события? Здесь, по существу, речь идет о том, чтобы найти условную вероятность 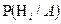для каждой гипотезы. Эта вероятность ищется по формуле Бейеса:

 

.
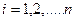