
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Случайные величины. Числовые характеристики случайных величинСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Два стрелка стреляют каждый по своей мишени, делая, независимо друг от друга по одному выстрелу. Вероятность попадания в мишень для первого стрелка Решение. Случайная величина Z имеет три возможных значения: -1, 0 и +1. Z= -1, если первый стрелок промахнулся, а второй попал; Z=0, если оба попали или оба промахнулись; Z=+1, если первый стрелок попал, а второй промахнулся. Следовательно,
где Ряд распределения величины Z имеет вид
Математическое ожидание равно
Дисперсию находим по формуле
Закон Пуассона Радиоаппаратура состоит из 1000 электроэлементов. Вероятность отказа одного элемента в течение одного года работы равна 0,001 и не зависит от состояния других элементов. Какова вероятность отказа двух и не менее двух электроэлементов за год? Решение. Считая случайное число Х отказавших элементов подчиняющимся закону Пуассона с параметром 1) вероятность отказа ровно двух элементов
2) вероятность отказа не менее двух элементов, вычисляется через противоположное событие
Показательный закон Электронная лампа работает исправно в течение случайного времени Т, распределенного по показательному закону Решение. Отказы ламп образуют простейший поток событий с плотностью а) в) Равномерный закон На перекрестке стоит автоматический светофор, в котором 1 минуту горит зеленый свет и 0,5 минуты – красный, затем опять 1 минуту горит зеленый свет, 0,5 минуту – красный и т.д. Некто подъезжает к перекрестку на машине в случайный момент, не связанный с работой светофора. Найти вероятность того, что он проедет перекресток, не останавливаясь. Решение. Момент проезда автомашины через перекресток распределен равномерно в интервале, равном периоду смены цветов в светофоре. Этот период равнее 1+0,5=1,5 минут. Для того, чтобы машина проехала через перекресток не останавливаясь, достаточно, чтобы момент проезда перекрестка пришелся на интервал времени (0;1). Для равномерно распределенной случайной величины в интервале (0;1,5) вероятность попасть в интервал (0;1) равна 2/3.
|
||||||||||||
|
Последнее изменение этой страницы: 2017-02-08; просмотров: 1619; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.117.254.177 (0.006 с.) |

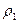 , для второго -
, для второго - 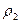 . Рассматривается случайная величина, которая равна разности между числом попаданий для первого и второго стрелка
. Рассматривается случайная величина, которая равна разности между числом попаданий для первого и второго стрелка  . Построить ряд распределения случайной величины Z и найти ее числовые характеристики
. Построить ряд распределения случайной величины Z и найти ее числовые характеристики 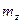 и
и  .
.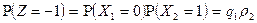 ;
;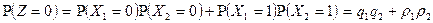 ;
; ,
,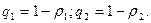
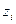
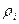
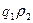

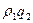
 =
=  .
. .
.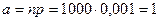 , получим:
, получим: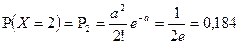 ;
;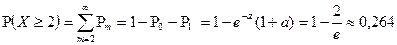 .
.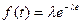 при
при 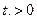 и равна 0 при
и равна 0 при 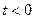 . По истечении времени Т лампа выходит из строя, после чего ее немедленно заменяют новой. Найти вероятность того, что за время
. По истечении времени Т лампа выходит из строя, после чего ее немедленно заменяют новой. Найти вероятность того, что за время 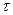 : а) лампу не придется заменять; б) лампу придется заменять ровно три раза; в) лампу придется заменять не менее трех раз.
: а) лампу не придется заменять; б) лампу придется заменять ровно три раза; в) лампу придется заменять не менее трех раз. . Математическое ожидание числа отказов за время
. Математическое ожидание числа отказов за время 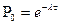 ; б)
; б) 
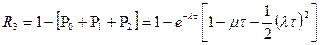 .
.


