
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Повторение опытов. Частная и общая теоремы. Формула Бернулли.
Производится несколько независимых опытов, в каждом из которых может появиться или не появиться некоторое событие А. Если опыты производятся в одинаковых условиях, то вероятность события А во всех опытах одна и та же, если опыты производятся в разных условиях, то вероятность события А от опыта к опыту меняется. Для первого случая применяется частная теорема для вычисления вероятности того, что событие А при n независимых опытах, в каждом из которых оно появляется с вероятностью p, появится ровно m раз, выражается формулой Бернулли:
где g = 1- p. Для второго случая применяется общая теорема о повторении опытов. Пусть производится n независимых опытов, в каждом из которых может появиться или не появиться некоторое событие А, причем вероятность появления события в i-м опыте равна p
где p Общую теорему о повторении опытов можно записать в виде следующей формулы:
Раскрывая скобки в левой части и выполняя приведение подобных членов, получим все вероятности:
2.3. Случайные величины и их законы распределения вероятностей.
Основные понятия и определения. Случайной величиной называется величина, которая в результате опыта может принять то или иное значение, причем неизвестно заранее, какое именно. Различают непрерывные случайные величины, дискретные и смешанные. Законом распределения случайной величины называется всякое соотношение, устанавливающее связь между возможными значениями случайной величины и соответствующими им вероятностями. Рядом распределения случайной величины называется закон распределения, представленный в виде таблицы, в которой перечислены возможные значения случайной величины и соответствующие им вероятности:
Функция распределения случайной величины X есть вероятность события X<x, где x – некоторая текущая переменная. Вероятность этого события, очевидно, зависит от x и, следовательно, является функцией и обозначается F(x):
Функция распределения обладает следующими свойствами: 1. Функция распределения F(x) есть неубывающая функция своего аргумента, т.е. при 2. На минус бесконечности функция распределения равна нулю: F(-∞)=0. 3. На плюс бесконечности функция распределения равна единице: F(+∞)=1. Плотность распределения случайной величины это функция f (x) – производная функции распределения – характеризует как бы плотность, с которой распределяются значения случайной величины в данной точке. Дифференциальная связь между функцией распределения и плотностью распределения имеет следующий вид:
Интегральная связь между функцией распределения и плотностью распределения имеет следующий вид:
Плотность распределения обладает следующими свойствами: 1. Плотность распределения есть неотрицательная функция: f (x)≥0. 2. Интеграл в бесконечных пределах от плотности распределения равен единице:
С помощью функции распределения и с помощью плотности распределения просто решается задача вычисления вероятности попадания случайной величины в определенный интервал: - через функцию распределения:
- через плотность распределения:
|
|||||||||||||||
|
Последнее изменение этой страницы: 2017-02-08; просмотров: 740; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.224.67.149 (0.008 с.) |
 С
С 
 ,
,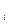 , а вероятность непоявления g
, а вероятность непоявления g  = 1- p
= 1- p  в выражении производящей функции:
в выражении производящей функции: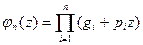 ,
,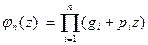 =
= 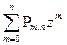 .
. как коэффициенты при нулевой, первой и т.д. степенях z.
как коэффициенты при нулевой, первой и т.д. степенях z.



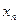




 .
.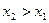
 .
. .
.
 .
. .
. . Вероятность этого события равна:
. Вероятность этого события равна: ;
;



