
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Показатели риска и методы его оценки.Содержание книги
Поиск на нашем сайте
Инструментом для проведения необходимых вычислений является математическая теория вероятностей. Каждому событию ставится в соответствие некоторая величина, характеризующую возможность того, что оно (событие) произойдет — вероятность данного события — р. Если событие не может произойти ни при каких условиях, его вероятность нулевая (р == 0). Если событие происходит при любых условиях, его вероятность равна единице. Если же в результате проведения эксперимента или наблюдения установлено, что некоторое событие происходит в n случаях из N, то ему приписывается вероятность р = n/N. Сумма вероятностей всех событий, которые могут произойти в результате некоторого эксперимента, должна быть равна единице. Перечисление всех возможных событий с соответствующими им вероятностями называется распределением вероятностей в данном эксперименте. Вероятность может быть выражена в процентах: р = (n/N)*100%, тогда значение р может находится в пределах от 0 до 100%. Количественно риск может быть охарактеризован как некий показатель, измеряющий вариабельность дохода или доходности, для этой цели можно использовать целый ряд статистических коэффициентов, в частности: размах вариации, дисперсию, среднее квадратическое отклонение, называемое иногда стандартным, и коэффициент вариации. Размахом вариации называется разность между максимальным и минимальным значениями признака ряда статистических величин х1, х2, х3, …, хn: R = xmax - xmin (7) Недостатки: 1) дает грубую оценку степени вариации значений признака; 2) является абсолютным показателем и потому его применение в сравнительном анализе весьма ограничено; 3)его величина слишком зависит от крайних значений ранжированного ряда. Дисперсия является средним квадратом отклонений значений признака от его средней и рассчитывается для ряда х1, х2, х3, …, хn по формуле: Д=σ2= где Среднее квадратическое отклонение показывает среднее отклонение значений варьирующего признака относительно центра распределения, в данном случае средней арифметической. Этот показатель рассчитывается по формуле: σ= Размах вариации (R), дисперсия (Д) и среднее квадратическое отклонение (σ) обладают одним общим недостатком - это абсолютные показатели, значение которых существенно зависит от абсолютных значений исходного признака ряда. Поэтому большее применение имеет коэффициент вариации, рассчитываемый по формуле: V= После определения степени риска необходимо им управлять, этим занимается риск-менеджмент, который представляют собой набор приемов управления риском.
Критерии степени риска.
Риск характеризуется несколькими главными показателями: 1. Безрисковая зона. Ей соответствуют нулевые потери или получение прибыли. 2. Зона допустимого риска – это область, в пределах которой данный вид предпринимательской деятельности сохраняет свою экономическую целесообразность, т.е. потери имеют место, но они меньше ожидаемой прибыли. Граница зоны допустимого риска соответствует уроню потерь равному расчетной прибыли от предпринимательской деятельности. 3. Зона критического риска – область, характеризующаяся возможностью потерь превышающих величину ожидаемой прибыли вплоть до величины полной расчетной выручки от предпринимательства. 4. Зона критического риска характеризуется опасностью потерь, которые заведомо превышают ожидаемую прибыль и в максимуме могут привести к невозмещаемой потери всех средств, вложенных предпринимателем в дело. 5. Зона катастрофического риска. Это область потерь, которые по своей величине превосходят критический уровень и в максимуме могут достигать величины равной имущественному состоянию предпринимателя. Катастрофический риск может привести к краху, банкротству, несостоятельности.
Уровни и значения критериев риска в предпринимательстве по Райзбергу
Оптимальный коэффициент риска 0,03 или 3% и ведущий к банкротству 0,07 при оценке финансовых операций.
|
||||
|
Последнее изменение этой страницы: 2017-02-07; просмотров: 185; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.133.122.95 (0.009 с.) |

 , (8)
, (8) (9)
(9)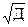 , (10)
, (10) (11)
(11)



