Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Энтропия. Статистический смысл второго начала термодинамикиСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Классическая термодинамика рассматривает происходящие процессы безотносительно к внутреннему строению системы; поэтому в рамках классической термодинамики показать физический смысл энтропии невозможно. Для решения этой проблемы Больцманом в теорию теплоты были введены статистические представления. Каждому состоянию системы приписывается термодинамическая вероятность (определяемая как число микросостояний, составляющих данное макросостояние системы), тем большая, чем более неупорядоченным или неопределенным является это состояние. Энтропия есть функция состояния, описывающая степень неупорядоченности системы. Количественная связь между энтропией S и термодинамической вероятностью W выражается формулой Больцмана:
С точки зрения статистической термодинамики второе начало термодинамики можно сформулировать следующим образом: Система стремится самопроизвольно перейти в состояние с максимальной термодинамической вероятностью. Статистическое толкование второго начала термодинамики придает энтропии конкретный физический смысл меры термодинамической вероятности состояния системы. 24. Реальный газ. Уравнение Ван-дер-Ваальса
Реальный газ — газ, который не описывается уравнением состояния идеального газа Клапейрона — Менделеева. Зависимости между его параметрами показывают, что молекулы в реальном газе взаимодействуют между собой и занимают определенный объём. Состояние реального газа часто на практике описывается обобщённым уравнением Менделеева — Клапейрона:
где: p — давление; V — объем; T — температура; Zr = Zr (p,T) — коэффициент сжимаемости газа; m — масса; М — молярная масса; R — газовая постоянная. Уравнение состояния газа Ван-дер-Ваальса — уравнение, связывающее основные термодинамические величины в модели газа Ван-дер-Ваальса. Для более точного описания поведения реальных газов при низких температурах была создана модель газа Ван-дер-Ваальса, учитывающая силы межмолекулярного взаимодействия. В этой модели внутренняя энергия Термическим уравнением состояния (или, часто, просто уравнением состояния) называется связь между давлением, объёмом и температурой. Рассмотрим сначала газ, в котором частицы не взаимодействуют друг с другом, такой газ удовлетворяет уравнению состояния идеального газа:
Частицы данного газа являются упругими сферами одинакового радиуса r. Так как газ находится в сосуде конечного объёма, то пространство, где могут перемещаться частицы, будет несколько меньше. В исходной формуле следует вычесть из всего объёма некую его часть b, которая, вообще говоря, зависит только от вещества, из которого состоит газ. Таким образом, получается следующее уравнение:
Вычитаемый объём b не будет в точности равен суммарному объёму всех частиц. Если частицы считать твёрдыми и абсолютно упругими шариками, то вычитаемый объём будет примерно в четыре раза больше. Это легко объясняется тем, что центры упругих шаров не могут приближаться на расстояние ближе Далее Ван-дер-Ваальс рассматривает силы притяжения между частицами газа и делает следующие допущения: · Частицы распределены равномерно по всему объёму. · Силы притяжения стенок сосуда не учитываются, что в общем случае неверно. · Частицы, находящиеся внутри сосуда и непосредственно у стенок, ощущают притяжение по-разному: внутри сосуда действующие силы притяжения других частиц компенсируют друг друга. Для частиц внутри сосуда силы притяжения не учитываются. А частицы, находящиеся непосредственно у края сосуда, затягиваются внутрь силой, пропорциональной концентрации:
Число частиц, которые находятся непосредственно у стенок, в свою очередь тоже предполагается пропорциональным концентрации n. Можно считать, что давление на стенки сосуда меньше на некоторую величину, обратно пропорциональную квадрату объёма:
Окончательное уравнение:
Для одного моля газа Ван-дер-Ваальса оно имеет вид:
где:
Это уравнение фактически является уравнением состояния идеального газа с двумя поправками. Поправка
Для
где:
Электростатическое поле. Поле точечного заряда (напряженность, потенциал, работа по переносу заряда в эл. поле, графическое представление поля). Закон Кулона. Принцип суперпозиции электрических полей Электрическое поле — пространство, обладающее свойством действовать с силой на электрический заряд, помещённый в это поле. Напряженность электрического поля E=F/Q где: F — сила, действующая на точечный положительный заряд Q, помещенный в данную точку поля. Сила, действующая на точечный заряд Q, помещенный в электрическое поле: F=QE Поток вектора напряженности Е электрического поля: а) через произвольную поверхность S, помещенную в неоднородное поле,
где: a — угол между вектором напряженности Е и нормалью n к элементу поверхности; dS — площадь элемента поверхности; En — проекция вектора напряженности на нормаль; б) через плоскую поверхность, помещенную в однородное электрическое поле, ФE=ЕScosa Поток вектора напряженности Е через замкнутую поверхность:
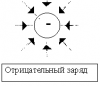
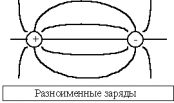
где интегрирование ведется по всей поверхности. Силовые линии (линии напряженности) - непрерывные (воображаемые) линии вектор напряженности касателен к каждой точке которых. Способ описания с помощью силовых линий введен Фарадеем. Свойства: 1. Начинаются на положительных и заканчиваются на отрицательных зарядах. 2. Не пересекаются. 3. Густота линий тем больше, чем больше напряженность. Т.е. напряженность поля прямо пропорциональна количеству силовых линий, проходящих через единицу площади поверхности. 4. Можно договориться изображать поля так, что количество проведенных линий пропорционально величине заряда.
Потенциал электрического поля есть величина, равная отношению потенциальной энергии точечного положительного заряда, помещенную в данную точку поля, к этому заряду; j=П/Q или потенциал электрического поля есть величина, равная отношению работы сил поля по перемещению точечного положительного заряда из данной точки поля в бесконечность к этому заряду: j=A/Q Потенциал электрического поля в бесконечности условно принят равным нулю. Работа, совершаемая электрическим полем при перемещении точечного заряда Q из одной точки поля, имеющей потенциал j1, в другую, имеющую потенциал j2, A=Q(j1—j2)
где: El — проекция вектора напряженности Е на направление перемещения; dl — перемещение. В случае однородного поля последняя формула принимает вид A=QElcosa, где: l — перемещение; a — угол между направлениями вектора Е и перемещения l. Закон Кулона. Модуль силы взаимодействия двух точечных зарядов в вакууме прямо пропорционален произведению модулей этих зарядов и обратно пропорционален квадрату расстояния между ними.
где: F — сила взаимодействия двух точечных зарядов Q1, и Q2; r — расстояние между зарядами; e — диэлектрическая проницаемость среды; e0 — электрическая постоянная:
Если поле в некоторой точке пространства создаётся отдельными точечными зарядами, то напряжённость результирующего поля Е равна векторной сумме напряженностей складываемых полей
Это правило получило название принципа суперпозиции электрических полей- результат воздействия на частицу нескольких внешних сил есть векторная сумма воздействия этих сил.. Подчеркнем ещё раз, что справедливость этого принципа подтверждена экспериментально. 26. Циркуляция вектора напряженности электрического поля. Связь напряженности и потенциала эл. поля
27. Теорема Гаусса для электрического поля и примеры её применения
28. Поле диполя. Диполь в однородном и неоднородном электрическом поле
|
||||
|
Последнее изменение этой страницы: 2017-02-06; просмотров: 433; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.191.97.133 (0.012 с.) |

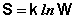

 становится функцией не только температуры, но и объёма.
становится функцией не только температуры, но и объёма.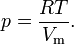
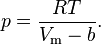
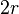 .
. .
.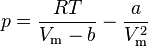


 — давление,
— давление, — молярный объём,
— молярный объём,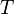 — абсолютная температура,
— абсолютная температура, — универсальная газовая постоянная.
— универсальная газовая постоянная. учитывает силы притяжения между молекулами (давление на стенку уменьшается, так как есть силы, втягивающие молекулы приграничного слоя внутрь), поправка
учитывает силы притяжения между молекулами (давление на стенку уменьшается, так как есть силы, втягивающие молекулы приграничного слоя внутрь), поправка 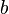 — объем молекул газа.
— объем молекул газа. молей газа Ван-дер-Ваальса уравнение состояния выглядит так:
молей газа Ван-дер-Ваальса уравнение состояния выглядит так: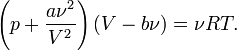
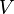 — объём.
— объём. или
или