
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Законы Ньютона в неинерциальных системах отсчетаСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Существование инерциальных систем отсчета лишь постулируется первым законом Ньютона. Реальные системы отсчета, связанные, например, с Землей или с Солнцем, не обладают в полной мере свойством инерциальности в силу их кругового движения. Описание же движения в неинерциальных системах отсчета, движущихся с ускорением относительно инерциальных, требует введения т. н. фиктивных сил таких как сила инерции, центробежная сила или сила Кориолиса. Эти «силы» не обусловлены взаимодействием тел, то есть по своей природе не являются силами и вводятся лишь для сохранения формы второго закона Ньютона: Классическая теория тяготения Ньютона (Закон всемирного тяготения Ньютона) — закон, описывающий гравитационное взаимодействие в рамках классической механики. Этот закон был открыт Ньютоном около 1666 года. Он гласит, что сила
Разложение сил. Разложение силы на составляющие основывается на правилах сложения сил. Целью разложения силы, приложенной к какому-либо телу, является определение сил взаимодействия между этим телом и другими телами, обычно связями, наложенными на него. Чтобы разложить силу, нужно задать некоторые из характеристик (величина, направление и точка приложения) составляющих сил. Точками приложения составляющих сил могут быть: 1) точка приложения раскладываемой силы и 2) точка соединения или соприкосновения тела, к которому приложена раскладываемая сила, с другими телами (связями). Направлениями для составляющих сил в большинстве случаев являются: 1) направления, по которым другие тела (связи) препятствуют перемещению тела или точки приложения раскладываемой силы, и 2) направления движения точки приложения раскладываемой силы или точек приложения составляющих сил. ЦЕНТР МАСС (центр инерции) системы материальных точек – условная (или эквивалентная) точка, представляющая собой одну из геометрических характеристик распределения масс в системе.
Понятие центра масс широко используется в различных разделах механики. Например, центр масс тела можно принять в качестве центра тяжести – точки приложения суммарной силы однородного поля тяжести, действующего на тело.Скорость центра масс, умноженная на суммарную массу системы, – это количество движения (импульс) этой системы.
Закон сохранения импульса
Выражение (2.9) представляет собой закон сохранения импульса: импульс замкнутой системы тел с течением времени не изменяется.
Другими словами, импульс системы равен произведению массы системы на скорость ее центра инерции.
или где
|
||||
|
Последнее изменение этой страницы: 2017-02-06; просмотров: 434; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.145.68.167 (0.007 с.) |

 ,где
,где  — сумма всех фиктивных сил, возникающих в неинерциальной системе отсчета.
— сумма всех фиктивных сил, возникающих в неинерциальной системе отсчета. гравитационного притяжения между двумя материальными точками массы
гравитационного притяжения между двумя материальными точками массы  и
и  , разделёнными расстоянием
, разделёнными расстоянием  , пропорциональна обеим массам и обратно пропорциональна квадрату расстояния между ними — то есть:
, пропорциональна обеим массам и обратно пропорциональна квадрату расстояния между ними — то есть:  или в векторной форме:
или в векторной форме:  вблизи земной поверхнос т и:
вблизи земной поверхнос т и: Здесь
Здесь 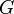 — гравитационная постоянная, равная
— гравитационная постоянная, равная  м³/(кг с²).
м³/(кг с²).
 Пусть
Пусть  – масса
– масса  -той (
-той ( ) точки системы, а
) точки системы, а  – радиус-вектор этой точки в некоторой системе координат. Тогда радиус-вектор
– радиус-вектор этой точки в некоторой системе координат. Тогда радиус-вектор  точки С – центра масс определяется по формуле
точки С – центра масс определяется по формуле ,
, 
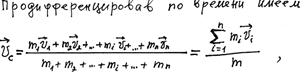




 представляет собой импульс всей системы. Таким образом,
представляет собой импульс всей системы. Таким образом,  или
или (2.9)
(2.9)


 масса системы.
масса системы.
 (2.10)
(2.10)

 (2.11)
(2.11) ускорение центра масс.
ускорение центра масс.


