
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Кинетическая энергия при плоском движенииСодержание книги
Поиск на нашем сайте
Плоским (плоскопараллельным) называется такое движение, при котором все точки тела движутся в параллельных плоскостях. Представим плоское движение тела как поступательное движение со скоростью В этом случае скорость i -той материальной точки тела определяется формулой
Кинетическая энергия i - той материальной точки равна
или
Просуммировав по всем материальным точкам, получим
или где М - полная масса тела, Если в качестве точки О взять центр масс тела С, то Таким образом, если разбить плоское движение тела на поступательное со скоростью центра масс V c и вращательное с угловой скоростью w вокруг оси, проходящей через центр масс тела, то кинетическая энергия распадается на два независимых слагаемых, одно из которых определяется только скоростью центра масс V c, а другое - угловой скоростью w. Из (13) следует, что при вращении тела относительно оси z, проходящей через центр масс С, его кинетическая энергия Пе́рвая косми́ческая ско́рость (кругова́я ско́рость) — минимальная скорость, которую необходимо придать объекту, чтобы вывести его на геоцентрическую орбиту. Часто для удобства вычисления первой космической скорости переходят к рассмотрению этого движения в неинерциальной системе отсчета — относительно Земли. В этом случае объект на орбите будет находиться в состоянии покоя, так как на него будут действовать уже две силы: центробежная сила и сила тяготения. Соответственно, для вычисления первой космической скорости необходимо рассмотреть равенство этих сил. Точнее, на тело действует одна сила - сила тяготения, она же - центростремительная. Центробежная сила действует на Землю. Центростремительная сила, вычисляемая из условия вращательного движения равна силе тяготения. Отсюда, приравнивая эти формулы, вычисляется скорость.
где m — масса объекта, M — масса планеты, G — гравитационная постоянная,
Втора́я косми́ческая ско́рость — наименьшая скорость, которую необходимо придать объекту (например, космическому аппарату), масса которого пренебрежимо мала по сравнению с массойнебесного тела (например, планеты), для преодоления гравитационного притяжения этого небесного тела и покидания замкнутой орбиты вокруг него. Предполагается, что после приобретения телом этой скорости оно более не получает негравитационного ускорения (двигатель выключен, атмосфера отсутствует). Запишем закон сохранения энергии где слева стоят кинетическая и потенциальная энергии на поверхности планеты (потенциальная энергия отрицательна, так как точка отсчета взята на бесконечности), справа то же, но на бесконечности (покоящееся тело на границе гравитационного влияния — энергия равна нулю). Здесь m — масса пробного тела, M — масса планеты, R — радиус планеты, G —гравитационная постоянная, v — вторая космическая скорость.Решая это уравнение относительно v 2, получим
|
||||
|
Последнее изменение этой страницы: 2017-02-06; просмотров: 281; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.14.132.178 (0.006 с.) |

 , некоторой точки 0 в нем и вращения вокруг оси, проходящей через эту же точку и перпендикулярной
, некоторой точки 0 в нем и вращения вокруг оси, проходящей через эту же точку и перпендикулярной  .
. .
.
 .
.
 , (12)
, (12) - радиус-вектор центра масс,
- радиус-вектор центра масс,  - момент инерции тела относительно оси, проходящей через точку О.
- момент инерции тела относительно оси, проходящей через точку О. и формула (12) упрощается:
и формула (12) упрощается:  . (13)
. (13) . (14)
. (14) ,
,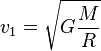 ,
, — первая космическая скорость, R — радиус планеты. Подставляя численные значения (для Земли M = 5,97·1024 кг, R = 6 371 км), найдем
— первая космическая скорость, R — радиус планеты. Подставляя численные значения (для Земли M = 5,97·1024 кг, R = 6 371 км), найдем 7,9 км/с
7,9 км/с




