
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Розділ 2. Методи розв’язку систем лінійних рівняньСодержание книги Похожие статьи вашей тематики
Поиск на нашем сайте Короткі теоретичні відомості Система лінійних алгебраїчних рівнянь (СЛАР) у загальному випадку має вигляд:
де Вводячи матрицю коефіцієнтів системи
та вектор-стовпчик вільних членів
Якщо всі вільні члени
Метод Гаусса Метод Гаусса або метод послідовного виключення невідомих – один з найвідоміших та широко застосовуваних прямих методів розв’язування СЛАР. Процес розв’язання даним методом поділяють на два етапи: перший – це зведення системи (2.3) до трикутного вигляду(2.4) (прямий хід):
Другий етап – це визначення невідомих за формулами (2.5) (зворотний хід);
На практиці обчислення методом Гаусса зручно проводити, скориставшись схемою єдиного ділення, яку подано в табл. 2.1. Таблиця 2.1.
Наприклад: Скориставшись схемою єдиного ділення розв’язати систему лінійних рівнянь методом Гаусса.
Розв’язок: Використовуючи схему єдиного ділення складемо таблицю:
Відповідь: х1 =1; х2 =2; х3 =3. Метод прогонки Даний метод реалізується у випадку, коли матриця Матрицю
Якій відповідає розширена матриця:
Якщо до (2.7) застосувати алгоритм прямого ходу метода Гаусса, то матриця
Враховуючи, що останній стовпчик цієї матриці відповідає правій частині матриці
Співвідношення (2.9) є формулою оберненого ходу, а коефіцієнти
Обернений хід метода прогонки починається з обчислення
Звідси Інші значення невідомих знаходять рекурентно за формулою (2.9). Алгоритм метода прогонки називається коректним, якщо для всіх Достатньою умовою коректності та стійкості даного метода є умова преобладания діагональних елементів у матриці
та у (2.11) має місце строга нерівність хоча б при одному Наприклад: Дана система лінійних алгебраїчних рівнянь яка складається з трьох діагональної матриці
Розв’язання. Перевіримо систему на умову преобладания діагональних елементів (2.11): у першому рівнянні Запишемо дане рівняння у вигляді матриці:
Прямий хід: Обчислимо прогоночні коефіцієнти:
Так як
Обернений хід:
Відповідь:
Метод LU – декомпозицій У цьому методі матриця коефіцієнтів А подається у вигляді добутку матриць L та U: A = LU, (2.12) де L – нижня трикутна матриця; а U – верхня трикутна матриця, усі діагональні елементи якої дорівнюють 1:
Метод LU -факторизації складається з двох етапів: 1) етапу факторизації матриці A; 2) етапу отримання розв’язку X. Вектор В у процесі факторизації не змінюється. Із виразів (2.12) та (2.13) випливає, що для i > j елементи матриці A можна виразити через елементи матриць L та U:
Із рівнянь (2.14) випливає, що факторизація матриці A виконується за n стадій. На кожній j -й стадії послідовно обчислюють елементи lij чергового j -го стовпчика матриці L за формулою
та елементи uji чергового j -го рядка матриці U за формулою
Із формул (2.15), (2.16) випливає, що на першій стадії елементи На практиці елементи матриць L та U в процесі розкладання розміщуються на місцях елементів матриці А, причому елементи
Після факторизації матриці A система буде мати вигляд LUX = B. (2.17) Позначимо Y = UX, тоді із (2.17) маємо рівняння LY = B. (2.18) Оскільки L – нижня трикутна матриця, то розв’язок системи (2.18) отримуємо прямою підстановкою:
Після цього залишається розв’язати ще систему з верхньою трикутною матрицею U, всі діагональні елементи якої дорівнюють 1: UX = Y. (2.19) Розв’язавши систему (2.19), остаточно отримаємо шуканий вектор X:
Наприклад: Розв’язати систему лінійних алгебраїчних рівнянь методом LU-декомпозицій.
Розв’язок: Виконаємо операцію факторизації:
при
при
при В результаті маємо дві трикутні матриці:
Розважимо систему
Звідси маємо: Розважимо систему
Звідси маємо: Відповідь:
Метод простих ітерацій Розв’яжемо перше рівняння системи (2.1) відносно
де Використовуючи позначення
систему (2.20) можна записати у матричному вигляді
Для розв’язання системи за допомогою формули На практиці при застосуванні методу простої ітерації за критерій зупинки обчислень вибирають збіжність за аргументом:
де D — задана абсолютна похибка обчислень або:
де Для збіжності ітераційного процесу методу простої ітерації достатньо, щоб матриця системи була діагонально домінуючою:
Наприклад: Нехай необхідно розв’язати систему рівнянь методом простої ітерації з абсолютною похибкою не більше 1%:
Перевіримо виконання умови (2.23):
Умова (2.23) виконується, отже система (2.24) може бути розв’язана методом простої ітерації. Ітераційна формула відповідно до
Виконаємо ітерацію.
Використовуючи норми
Потрібна точність не досягнута, виконуємо наступну ітерацію:
Потрібна точність не досягнута, виконуємо наступну ітерацію:
Необхідна точність досягнута. Для порівняння, точний розв’язок системи
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2017-02-06; просмотров: 569; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.137 (0.013 с.) |

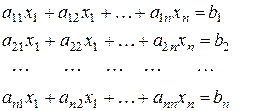 (2.1)
(2.1) - коефіцієнти системи,
- коефіцієнти системи,  - вільні члени системи,
- вільні члени системи,  - невідомі, які необхідно визначити.
- невідомі, які необхідно визначити.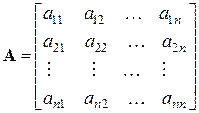 ,
,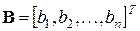 , ф також вектор-стовпчик невідомих
, ф також вектор-стовпчик невідомих  , систему (2.1) можна подати у матричній формі:
, систему (2.1) можна подати у матричній формі: . (2.2)
. (2.2) , то
, то  СЛАР називається однорідною. Із курсу лінійної алгебри відомо, що неоднорідна СЛАР має єдиний розв’язок у випадку, коли
СЛАР називається однорідною. Із курсу лінійної алгебри відомо, що неоднорідна СЛАР має єдиний розв’язок у випадку, коли 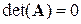 , де
, де  - визначник матриці
- визначник матриці 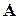 .
. (2.3)
(2.3)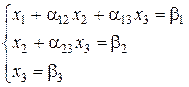 (2.4)
(2.4)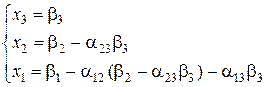 (2.5)
(2.5)



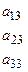






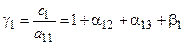



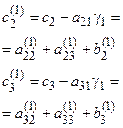





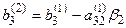
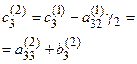



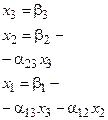




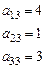

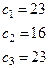

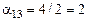

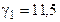


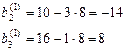

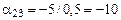



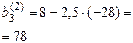
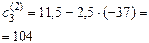


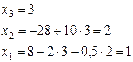

 ,
,  ,
,  , (2.6)
, (2.6)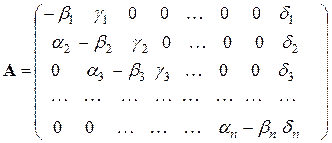 (2.7)
(2.7)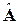 :
: (2.8)
(2.8) ,
, 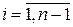 . (2.9)
. (2.9) ,
, 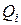 - називаються прогоночними та визначаються:
- називаються прогоночними та визначаються: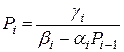 ,
,  ,
,  . Для цього використовують останнє рівняння, коефіцієнти якого визначено у прямому ході:
. Для цього використовують останнє рівняння, коефіцієнти якого визначено у прямому ході: ,
,  .
. , тобто
, тобто  .
. , та стійким, якщо
, та стійким, якщо  ,
,  та
та 
 :
: (2.11)
(2.11) .
. :
:
 . Розв’язати дану систему методом прогонки.
. Розв’язати дану систему методом прогонки. ; у другому рівнянні
; у другому рівнянні  ; у третьому
; у третьому  ; у четвертому
; у четвертому  , отже умова (2.11) виконується.
, отже умова (2.11) виконується.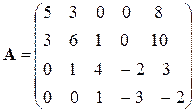 .
. ;
;  ;
; ;
;  .
. , то виходячи з (2.6) у другому доданку візьмемо від’ємний знак:
, то виходячи з (2.6) у другому доданку візьмемо від’ємний знак: ;
;  .
. ;
; ;
;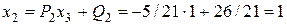 ;
;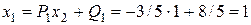 .
. .
.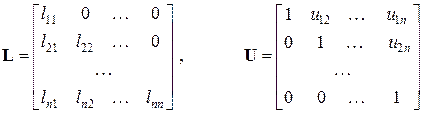 . (2.13)
. (2.13) (2.14)
(2.14) , (2.15)
, (2.15)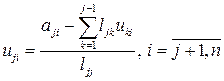 . (2.16)
. (2.16) , а
, а  .
.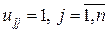 не запам’ятовуються. Таким чином, факторизована форма матриці А має вигляд
не запам’ятовуються. Таким чином, факторизована форма матриці А має вигляд .
. .
. .
.










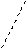







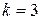
 :
:
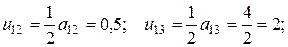

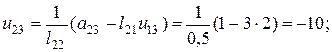
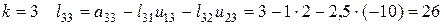 .
. ,
, 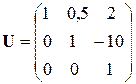 .
. :
: або
або 

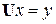 :
: або
або 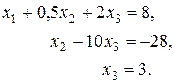

 .
. , друге відносно
, друге відносно  і так далі. В результаті отримаємо систему рівнянь еквівалентну системі (2.1):
і так далі. В результаті отримаємо систему рівнянь еквівалентну системі (2.1): (2.20)
(2.20) ,
,  при
при  ,
,  при
при 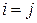 .
.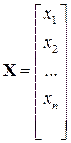 ,
,  ,
, 
 . Таким чином, метод простої ітерації є частковим випадком методу
. Таким чином, метод простої ітерації є частковим випадком методу  коли матриця С дорівнює:
коли матриця С дорівнює:
 . В якості такого наближення можна вибрати
. В якості такого наближення можна вибрати 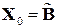 .
.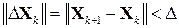 , (2.21)
, (2.21) , (2.22)
, (2.22) ‑ задана відносна похибка обчислень.
‑ задана відносна похибка обчислень. . (2.23)
. (2.23)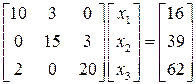 (2.24)
(2.24)
 .
. .
. , перевіримо досягнуту похибку розв’язку:
, перевіримо досягнуту похибку розв’язку: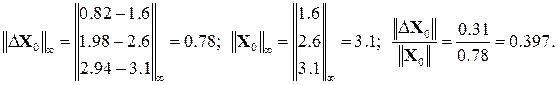
 .
.
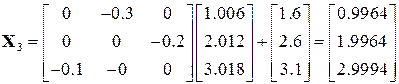 .
.
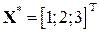 .
.


