Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Розділ 5. Стеми нелінійних рівнянь
Короткі теоретичні відомості
Нехай дана система
де
Метод простих ітерацій Нехай задано систему рівнянь з двома невідомими:
Треба знайти дійсні корені з потрібною мірою точності. Подамо систему (5.2) у вигляді:
Нехай
Аналогічно побудуємо послідовні наближення
Якщо ітераційний процес(5.5) збігається, тобто якщо існують границі:
то граничні значення
де М – найбільше з чисел Якщо M<0,5, то збіжність методу вважають гарною. При цьому Якщо виконуються умови:
із теореми про умови збіжності ітераційного процесу, то процес послідовних наближень (5.5) збігається до розв’язку Наприклад: Знайти з точністю до
Розв’язок: Зведемо систему до вигляду:
Перевіримо чи виконуються умови збіжності ітераційного процесу:
В даному випадку було прийнято Обчислимо значення похідних у наближених точках з області
Отже,
Таким чином умови збіжності виконуються. Послідовні наближення знайдемо за формулами:
Обчислення послідовних наближень зручно подати у вигляді табл.5.1. Таблиця 5.1.
Відповідь:
Метод Зейделя Нехай задано систему нелінійних рівнянь (5.1). Потрібно знайти дійсні корені з потрібною точністю. Систему рівнянь потрібно звести до вигляду (5.3). Візьмемо за початково наближене коренів деяке
Даний процес повторюється до тих пір поки не буде виконуватися умова Наприклад: Знайти з точністю до
Розв’язок: Зведення системи до вигляду (5.3), та пошук початкового наближення показано у попередньому прикладі. Задамо начальне наближене Послідовні наближення знайдемо за формулами (5.8):
Обчислення послідовних наближень зручно подати у вигляді табл.5.2. Таблиця 5.2.
Відповідь:
Метод Ньютона Розглянемо систему нелінійних рівнянь (5.1). Нехай
лінійну відносно
Систему (5.10) записують у векторній формі
де
Тоді процес розв’язання нелінійної системи подають у вигляді ітераційної процедури:
Можна показати, що для метода Ньютона розв’язання СНУ справедлива оцінка
де
Критерієм зупинки ітераційного процесу є збіжність за аргументом:
де e – задана відносна похибка або збіжність за функцією
де D – задана абсолютна похибка розв’язку. На практиці корисно поєднувати перевірки за обома критеріями. Наприклад: Знайти розв’язок системи рівнянь Для даної системи
Виберемо початкове наближення
Для порівняння, точні розв’язки цієї системи –
Контрольні завдання 1. Вибрати із табл. 5.3 систему рівнянь відповідно до свого варіанта. 2. Розв’язати систему методом Зейделя з похибкою, не більшою 1 %. 3. Розв’язати систему методом Ньютона з похибкою, не більшою 1 %. 4. Порівняти результати розв’язків різними методами. Варіанти завдань
Таблиця 5.3. Системи нелінійних рівнянь
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2017-02-06; просмотров: 235; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.222.67.251 (0.023 с.) |
 нелінійних рівнянь з
нелінійних рівнянь з  (5.1)
(5.1) ,
, 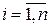 - функції дійсних змінних
- функції дійсних змінних  . Потрібно знайти дійсні корені з потрібною мірою точності.
. Потрібно знайти дійсні корені з потрібною мірою точності. (5.2)
(5.2) (5.3)
(5.3) і
і  - початкові наближення коренів, отримані графічно чи іншим способом, наприклад, грубим прикиданням. Підставивши в праві частини рівнянь системи (5.3) замість
- початкові наближення коренів, отримані графічно чи іншим способом, наприклад, грубим прикиданням. Підставивши в праві частини рівнянь системи (5.3) замість 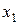 і
і  початкові значення
початкові значення  (5.4)
(5.4) (5.5)
(5.5) ,
, і
і  є коренями системи (5.3). Оцінка похибки n-го наближення визначається нерівністю:
є коренями системи (5.3). Оцінка похибки n-го наближення визначається нерівністю:
 і
і  , які входять у нерівності (5.6) чи (5.7).
, які входять у нерівності (5.6) чи (5.7). , так що в двох послідовних наближеннях збігаються, наприклад, перші три десяткових знаки після коми, то похибка останнього наближення не перевищує 0,001.
, так що в двох послідовних наближеннях збігаються, наприклад, перші три десяткових знаки після коми, то похибка останнього наближення не перевищує 0,001. (5.6)
(5.6) (5.7)
(5.7)
 корені рівняння взявши за початкові значення
корені рівняння взявши за початкові значення  :
: .
.




 .
. :
:

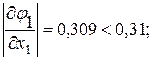
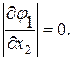







 , та
, та  . Обчислення
. Обчислення  здійснюється за формулами:
здійснюється за формулами: (5.8)
(5.8) , тоді
, тоді  .
. .
.





 – k -те наближення до розв’язку задачі (5.2). Розкладемо кожну функцію
– k -те наближення до розв’язку задачі (5.2). Розкладемо кожну функцію  у ряд Тейлора в околі точки X=X k і обмежимося лінійними членами рядів. Тоді замість системи (5.1) маємо наближену систему рівнянь:
у ряд Тейлора в околі точки X=X k і обмежимося лінійними членами рядів. Тоді замість системи (5.1) маємо наближену систему рівнянь: , (5.9)
, (5.9) . Розв’язок системи (5.9) вважатимемо за наступне наближення до розв’язку
. Розв’язок системи (5.9) вважатимемо за наступне наближення до розв’язку  . Тоді
. Тоді . (5.10)
. (5.10) ,
, ,
,  – матриця Якобі
– матриця Якобі

 , (5.11)
, (5.11) ,
,  — матриця Гессе. Таким чином, якщо матриця Якобі — невироджена, а другі похідні — неперервні, то за умови достатньої близькості початкового наближення до кореня метод Ньютона має квадратичну збіжність.
— матриця Гессе. Таким чином, якщо матриця Якобі — невироджена, а другі похідні — неперервні, то за умови достатньої близькості початкового наближення до кореня метод Ньютона має квадратичну збіжність. (5.12)
(5.12) (5.13)
(5.13)

 . Для оцінювання похибки у (5.12) та (5.13) використаємо евклідові норми
. Для оцінювання похибки у (5.12) та (5.13) використаємо евклідові норми  Тоді маємо:
Тоді маємо: