
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Розділ 6. Числене інтегрування функції ⇐ ПредыдущаяСтр 7 из 7
Короткі теоретичні відомості Формули Ньютона – Котеса Формули Ньютона – Котеса одержують інтегруванням інтерполяційних поліномів, побудованих за рівномірною сіткою. Розрізняють формули відкритого і закритого типів. У формулах закритого типу у розрахунках використовують значення функції, обчислені в обох кінцях елементарного відрізка, а у формулах відкритого типу, принаймні, одне зі значень участі у розрахунках не бере. Розглянемо побудову формули Ньютона – Котеса m- го порядку закритого типу. Для цього розіб’ємо елементарний відрізок [ xi, xi +1] на m рівних частин і обчислимо значення функції у вузлах
де Тоді, інтегруючи (6.1) і виконуючи заміну змінних
де cj – коефіцієнти Котеса, дорівнюють
Формулу (6.3) називають квадратурною формулою Ньютона – Котеса. З виразу (6.3) випливає, що коефіцієнти Котеса cj не залежать від функції f (x). Тоді, вважаючи, що
Крім цього, з (6.3) випливає, що
Отже, коефіцієнти Котеса симетричні відносно центра елементарного відрізка. Значення коефіцієнтів Котеса до десятого порядку включно наведено у табл. 6.1.
Похибка формули Ньютона – Котеса оцінюють як
Коефіцієнти Котеса розраховують за формулою
Зазначимо, що формули Ньютона – Котеса парного порядку за рахунок симетрії розбиття елементарного відрізка мають додатковий порядок точності. З цієї причини найчастіше використовують формули парного порядку. Із формули (6.4) випливає, що для зменшення похибки квадратурної формули Ньютона – Котеса необхідно збільшувати її порядок. Однак формули з Таблиця 6.1. Постійні для розрахунку коефіцієнтів Котеса і похибка формули Ньютона – Котеса порядку m.
Нариклад. Обчислимо інтеграл
Якщо у формулу Ньютона-Котеса прийняти
та називається формулою трапецій. У загальному вигляді формулу трапецій можна записати так:
Похибка даного методу обчислення:
де Якщо значення функції задано таблично, то похибка:
де Наприклад: Обчислити значення функції Розв’язок: Визначимо число кроків інтегрування
Розрахунки
Запишемо значення х до загальної формули:
Відповідь: І=0,7444. При
і називатиметься формулою Сімпсона або парабол. Загальна формула обчислення:
де
Похибка обчислення:
Якщо функція задана таблично, то похибка метода парабол:
де Наприклад: Обчислити значення функції Розв’язок:
Складемо таблицю підінтегральної функції
тоді Відповідь: І=0,74685. Наприклад: Визначити інтеграл методами трапецій та Сімпсона, який задано таблично. Оцінити похибку розрахунку.
Розв’язок:
Виходячи із значення х, крок інтегрування h=(x Виходячи із формули трапеції:
Похибка метода трапецій:
Знайдемо
Оцінка похибки за методом Сімпсона:
Порівнюючи обидва методи, можна зробити висновок, що метод Сімпсона дає більш точне значення визначеного інтеграла. Відповідь: Ітрапеції=50554, Rтрапеції=11; Ісімпсона=50567, Rсімпсона=-0,14. Ще однією формулою чисельного інтегрування, яка будується заміною підінтегральної функції інтерполяційним поліномом, може бути формула Ньютона загальний вигляд якої:
У формулі Ньютона кількість під інтегралів Формули Чебишова Як вже було показано, у формулах Ньютона – Котеса вузли інтерполяції розміщуються рівномірно, а вагові коефіцієнти обчислюють так, щоб формула була точною для полінома степеня, не нижчого m. У формулах Чебишова всі вагові коефіцієнти задають однаковими, а вузли вибирають так, щоб формула була точною для полінома степеня, не нижчого від m + 1. Ураховуючи, що формула має бути точною для f (x) º 1, із (6.3) маємо:
Для визначення вузлів x i , j проведемо в (6.5) заміну змінних
тоді
Із рівняння (6.5) одержуємо
Уведемо позначення
Для визначення вузлів
Із виразів (6.9) можна знайти
Методи Чебишова мають порядок точності m + 2. Наприклад: Обчислимо інтеграл Згідно з (6.6) знайдемо розташування вузлів формули Чебишова:
За формулою (6.6) обчислимо наближене значення інтегралу:
Формули Гаусса На відміну від формул Ньютона – Котеса та Чебишова у виведеній з виразу (6.2) формулі Гаусса вузли і вагові коефіцієнти не задаються, а визначаються так, щоб формула була точною для полінома найвищого можливого степеня. Можна показати, що ця вимога виконується, якщо вузли обчислюються за формулою (6.6), причому tj є коренями полінома Лежандра Pm +1(t) степеня m + 1, а вагові коефіцієнти обчислюються за формулою:
Поліноми Лежандра знаходять за виразом
або за рекурентною формулою
Деякі значення параметрів формули Гаусса для методів 1–4-го порядків наведено нижче:
Методи Гаусса мають порядок точності 2 m + 1. Нариклад: Обчислимо інтеграл
Згідно з (6.6) знайдемо розташування вузлів формули Гаусса:
Тоді згідно з формулою (6.2) маємо
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2017-02-06; просмотров: 382; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.218.168.16 (0.048 с.) |
 де
де 
 . Побудуємо інтерполяційний поліном Лагранжа на відрізку [ xi, xi +1] по вузлах
. Побудуємо інтерполяційний поліном Лагранжа на відрізку [ xi, xi +1] по вузлах 
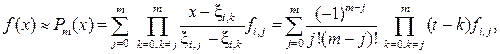 (6.1)
(6.1) .
. одержимо
одержимо , (6.2)
, (6.2) . (6.3)
. (6.3) , з (6.2) маємо
, з (6.2) маємо .
. .
. (6.4)
(6.4) .
. рідко використовують через їх числову нестійкість, що призводить до різкого зростання обчислювальної похибки. Причиною такої нестійкості є те, що коефіцієнти cj у формулі (6.2) при великих m мають різні знаки. Деякі коефіцієнти стають від’ємними при m = 8. Для m = 9 вони всі додатні, але для
рідко використовують через їх числову нестійкість, що призводить до різкого зростання обчислювальної похибки. Причиною такої нестійкості є те, що коефіцієнти cj у формулі (6.2) при великих m мають різні знаки. Деякі коефіцієнти стають від’ємними при m = 8. Для m = 9 вони всі додатні, але для 









 . Точне значення інтеграла
. Точне значення інтеграла 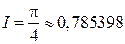 . За формулою Ньютона – Котеса 4-го порядку згідно з (6.2) для одного елементарного відрізка маємо
. За формулою Ньютона – Котеса 4-го порядку згідно з (6.2) для одного елементарного відрізка маємо
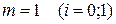 , то формула (6.3) матиме наступний вигляд:
, то формула (6.3) матиме наступний вигляд: ;
;  , а сама формула (6.2) виглядатиме:
, а сама формула (6.2) виглядатиме: 
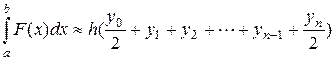 ,
,
 –максимальне значення функції другої похідної функції на заданому відрізку.
–максимальне значення функції другої похідної функції на заданому відрізку. ,
, –середнє арифметичне значення різниці другого порядку.
–середнє арифметичне значення різниці другого порядку. за допомогою метода трапецій із заданою точністю до
за допомогою метода трапецій із заданою точністю до  0,01.
0,01.
 ,
,  2, звідси
2, звідси 
 занесемо до таблиці:
занесемо до таблиці: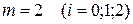 коефіцієнти Котеса дорівнюють:
коефіцієнти Котеса дорівнюють: ;
;  ;
; 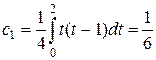 , тобто формула (6.2) матиме вигляд:
, тобто формула (6.2) матиме вигляд: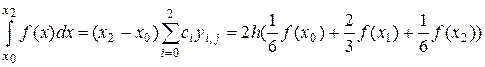
 ,
, - сума першого та останнього значення функції;
- сума першого та останнього значення функції; - сума непарних значень функції;
- сума непарних значень функції; - сума парних значень функції.
- сума парних значень функції. ,
, – четверта похідна заданої функції.
– четверта похідна заданої функції. ,
, –середнє арифметичне значення кінцевої різниці четвертого порядку.
–середнє арифметичне значення кінцевої різниці четвертого порядку.
 =1/12((1,0+0,36788)+4·(0,93941+0,56978)+2·0,7788)=0,74685.
=1/12((1,0+0,36788)+4·(0,93941+0,56978)+2·0,7788)=0,74685.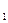 -x
-x  ) =150, n=11.
) =150, n=11.
 за формулою Сімпсона:
за формулою Сімпсона:



 таблично:
таблично:






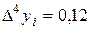

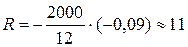


 Із залишковим членом:
Із залишковим членом:  , або для функції заданої таблично
, або для функції заданої таблично  .
. передбачається кратним 3.
передбачається кратним 3. ,
, . (6.5)
. (6.5) ,
, . (6.6)
. (6.6) . (6.7)
. (6.7) . Тоді з (6.7)
. Тоді з (6.7) . (6.8)
. (6.8) використовуємо умову, що формула (6.8) є точною для поліномів
використовуємо умову, що формула (6.8) є точною для поліномів  . Підставляючи ці функції в (6.8), одержуємо систему рівнянь:
. Підставляючи ці функції в (6.8), одержуємо систему рівнянь: (6.9)
(6.9) , а потім з (6.9) – x i , j . Нижче наведено tj для порядків
, а потім з (6.9) – x i , j . Нижче наведено tj для порядків  :
:
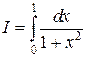 з попереднього прикладу методом Чебишова третього порядку за одним елементарним відрізком.
з попереднього прикладу методом Чебишова третього порядку за одним елементарним відрізком.


 ,
,




 методом Гауса 3-го порядку за одним елементарним відрізком,
методом Гауса 3-го порядку за одним елементарним відрізком, 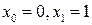 .
.





