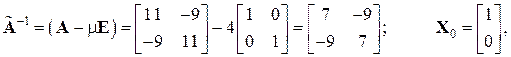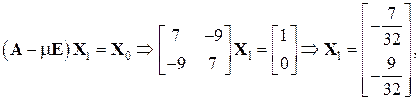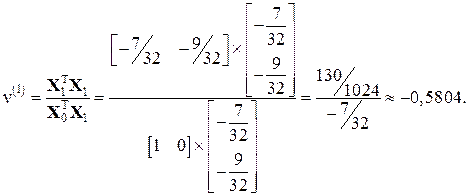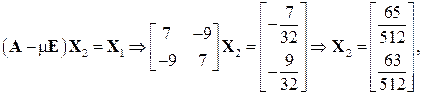Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Інтераційний метод Гаусса-Зейделя.
Сутність даного методу викладемо для СЛАР (2.3). Припустимо, що
Нехай ( Підставивши обчисленні значення
Ітераційний процес триває доти, поки не виконуватимуться нерівності
де Загальний випадок k -те наближення визначається:
Наприклад: Розв’язати систему лінійних рівнянь з точністю до 0,01 за допомогою ітераційного методу Гаусса-Зейделя.
Розв’язок: Для даної системи умови
Розв’яжемо перше рівняння системи відносно х1, друге – відносно х2, третє – відносно х3:
чи, виконавши ділення, одержимо:
За нульові наближення, візьмемо відповідні значення вільних членів системи: Знайдемо перші наближення, користуючись формулами (2.28-2.30)
Занесемо послідовність наближених коренів системи в таблицю:
Другі наближення:
і т.д. Наступні наближення наведено в таблиці, з якої випливає, що для ітерацій 2 і 3 виконується нерівність:
Відповідь: Контрольне завдання 1. Вибрати СЛАР відповідно до свого варіанта. 2. Розв’язати вибрану СЛАР методом Гаусса. 4. Розв’язати вибрану СЛАР методом прогонки. 5. Розв’язати вибрану СЛАР методом LU -декомпозицій. 6. Розв’язати вибрану СЛАР методом простої ітерації з похибкою не більше 1%. 7. Розв’язати вибрану СЛАР методом Гаусса-Зейделя з похибкою не більше 1%. 8. Порівняти результати розв’язування різними методами. Оцінити відхил розв’язку. Варіанти завдань
Розділ 3. ВЛАСНІ ЧИСЛА І ВЛАСНІ ВЕКТОРИ Короткі теоретичні відомості
Розглянемо квадратну матрицю
Власні числа
де Е – одинична матриця; Ψ – власний вектор матриці А, що відповідає деякому власному числу li. Із рівнянь (3.1), (3.2) випливає, що власні числа можна визначити з характеристичного рівняння:
З останнього рівняння випливає, що будь-яка матриця n´n має n власних чисел з урахуванням їх кратності. Множина власних чисел матриці називається її спектром. Визначивши власні числа, з умови (3.2) можна знайти власні вектори. Однак у разі великих розмірностей матриці А складність розрахунку значно зростає. Тому розроблено ряд спеціальних методів, що полегшують розв’язання задачі на власні числа і власні вектори.
Степеневий метод Розглянемо типову задачу відшукання максимального за модулем власного значення. Нехай { Ψ n }– система власних векторів, а {li} – система власних значень матриці А:
Нехай власні значення розташовані з урахуванням їх кратності в порядку зростання:
Задамо деяке початкове наближення X0 до вектора Ψ n і будемо послідовно обчислювати вектори X k = A X k–1, k = 1, 2… (3.4) Оскільки система власних векторів { Ψ i } повна, то X0 можна подати у вигляді
де c i – коефіцієнти розкладання. Тоді з (3.3), (3.4) маємо:
З огляду на те, що | ln | > | ln–1 |, для досить великих k з (3.5) маємо
Із виразу (3.6) випливає, що якщо cn ¹ 0, то при досить великому k
Отже, максимальне за модулем власне значення ln можна знайти з ітераційного процессу (3.4). При цьому k -те наближення
а k -те наближення до власного вектора Ψ
Критерієм зупинки ітераційного процесу (3.4) є виконання умови
де e – задане значення відносної похибки. Якщо треба знати знак ln, то його знаходять за формулою
Із виразів (3.2) та (3.5) випливає, що швидкість збіжності ітераційного процесу лінійна і визначається відношенням
Для стійкості числового процесу необхідно час від часу нормувати вектор Xk, щоб ||Xk|| = 1. Інакше, якщо | ln | > 1, то, як випливає з виразу (3.6), ||Xk|| ® ¥ якщо k
Для пошуку мінімального за модулем власного числа використовують той факт, що мінімальне за модулем власне число матриці A дорівнює величині, оберненій до максимального за модулем власного числа оберненої матриці А -1. Це дозволяє обчислити максимальне за модулем власне число lmaxinv матриці А -1, а потім знайти шукане мінімальне за модулем власне число матриці А з виразу Проте обчислення оберненої матриці – складна операція, яка у разі числової реалізації призводить до значної похибки внаслідок округлення. Тому на практиці під час пошуку мінімального за модулем власного числа чергове наближення вектора X k знаходять не з ітераційного процесу X k= A -1 · Xk–1, а з розв’язку системи лінійних рівнянь AX k = X k–1. При цьому m -те наближення
Наприклад: Знайдемо максимальне і мінімальне власні числа та відповідні їм власні вектори для матриці Нехай
Далі обчислимо мінімальне за модулем власне число і відповідний власний вектор. Нехай
Метод скалярного добутку Для симетричної матриці А максимальне за модулем власне число доцільно шукати з ітераційного процесу:
де k – номер ітерації; Найменше за модулем власне число симетричної матриці А шукають з ітераційного процесу:
де k – номер ітерації; Можна показати, що метод скалярного добутку має квадратичну збіжність, тобто Наприклад: Знайдемо максимальне і мінімальне власні числа та відповідні їм власні вектори для матриці з попереднього прикладу Нехай
Далі обчислимо мінімальне за модулем власне число і відповідний власний вектор. Нехай
Метод Віландта Часто в практичних задачах виникає необхідність знаходження власного числа, яке є найближчим до деякого заданого числа m. У такому випадку можна розв’язати задачу за допомогою методу Віландта. Суть методу полягає в тому, що спочатку знаходять деяку додаткову матрицю
Наприклад: Знайдемо власне число матриці
Контрольне завдання 1. Вибрати матрицю A як матрицю коефіцієнтів СЛАР контрольного завдання другого розділу відповідно до свого варіанта. 2. Знайти максимальне і мінімальне власні числа матриці та відповідні власні вектори степеневим методом та методом скалярного добутку з похибкою не більше 1 %.
3. Знайти власне число матриці, найближче до заданого числа m з похибкою не більше 1 %. Значення числа m вибрати з табл. 3.1 відповідно до варіанта. 4. Оцінити число обумовленості матриці. 5. Порівняти результати розв’язку різними методами. Таблиця 3.1. Значення числа m
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2017-02-06; просмотров: 492; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.188.142.146 (0.077 с.) |
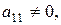
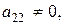
 тоді:
тоді: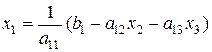 (2.25)
(2.25)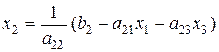 (2.26)
(2.26)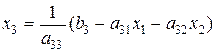 (2.27)
(2.27)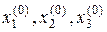 ) – деякий грубо наближений розв’язок системи. Назвемо цю сукупність чисел початковим наближенням. За початкове наближення можна взяти нульові значення змінних
) – деякий грубо наближений розв’язок системи. Назвемо цю сукупність чисел початковим наближенням. За початкове наближення можна взяти нульові значення змінних 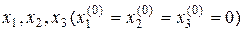 чи значенням вільних членів
чи значенням вільних членів 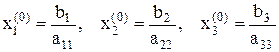 .
.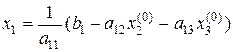 (2.28)
(2.28)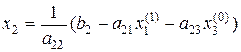 (2.29)
(2.29)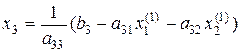 (2.30)
(2.30)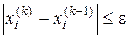 (і =1,2,3),
(і =1,2,3),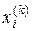 і
і 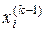 - два послідовних наближених;
- два послідовних наближених;  - задана точність.
- задана точність.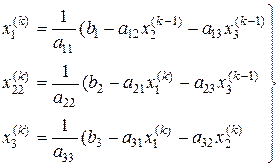
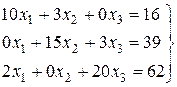
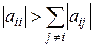 (i,j = 1,2,3) збіжності ітераційного процесу виконуються:
(i,j = 1,2,3) збіжності ітераційного процесу виконуються: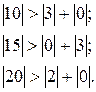
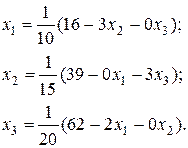
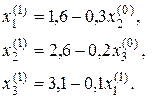
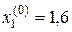 ;
; 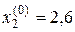 ;
; 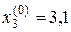 .
.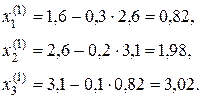



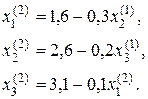
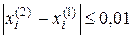 (i =1,2).
(i =1,2).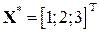 .
.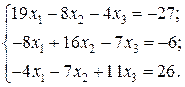
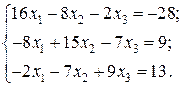
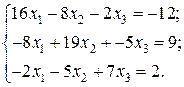
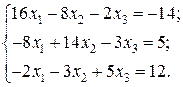
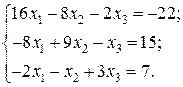
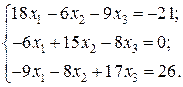
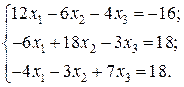
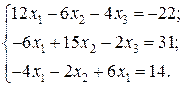
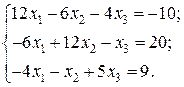
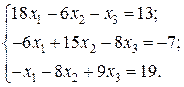
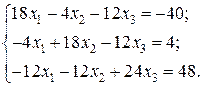
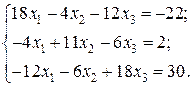
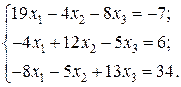
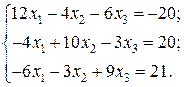
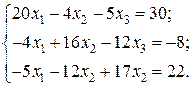
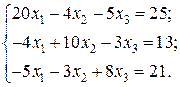
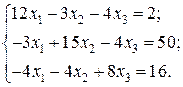
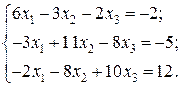
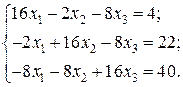
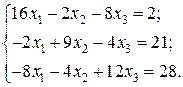
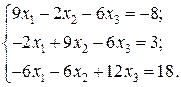
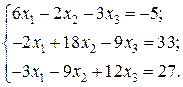
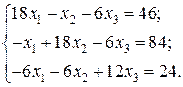
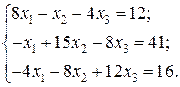

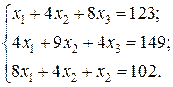
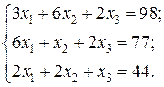
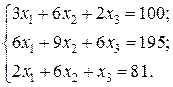
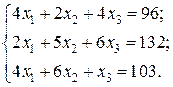
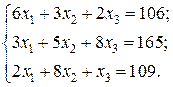
 -го порядку:
-го порядку: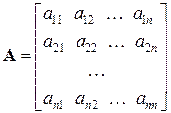 . (3.1)
. (3.1)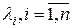 квадратної матриці
квадратної матриці 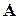 є дійсними або комплексними числами, що задовольняють умові:
є дійсними або комплексними числами, що задовольняють умові: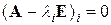 , (3.2)
, (3.2)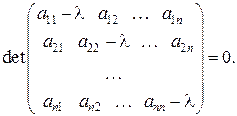
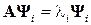 . (3.3)
. (3.3)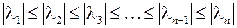 .
.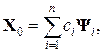
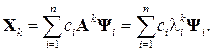 (3.5)
(3.5)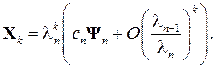 (3.6)
(3.6)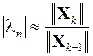 .
.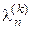 до власного значення ln оцінюють як
до власного значення ln оцінюють як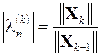 ,
,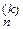 :
: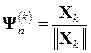 . (3.7)
. (3.7)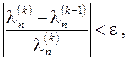
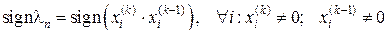 .
.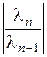 , оскільки
, оскільки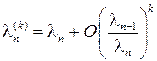 .
.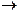 ¥. Тому за досить великого k може відбутися переповнення розрядної сітки обчислювальної системи. Якщо |ln| < 1, то ||Xk||
¥. Тому за досить великого k може відбутися переповнення розрядної сітки обчислювальної системи. Якщо |ln| < 1, то ||Xk|| 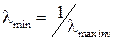 .
. до власного значення lmin можна оцінити так:
до власного значення lmin можна оцінити так: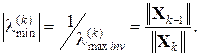
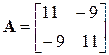 , яка має власні числа l1 = 2, l2 = 20 та відповідні їм власні вектори Ψ
, яка має власні числа l1 = 2, l2 = 20 та відповідні їм власні вектори Ψ 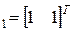 , Ψ
, Ψ 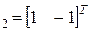 . Спочатку знаходимо максимальне за модулем власне число та відповідний вектор.
. Спочатку знаходимо максимальне за модулем власне число та відповідний вектор.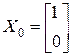 . Тоді згідно з виразом (3.4) маємо:
. Тоді згідно з виразом (3.4) маємо: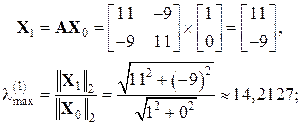
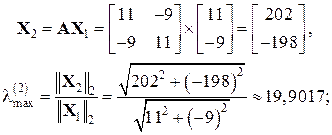

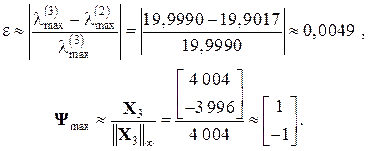
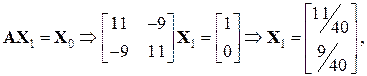
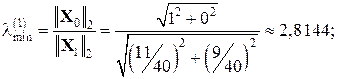
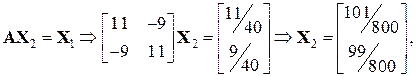
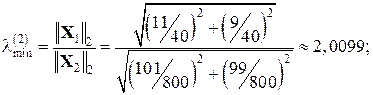
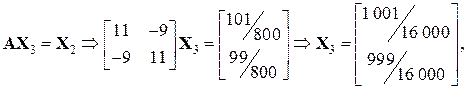
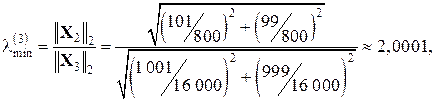
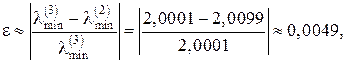
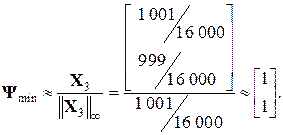
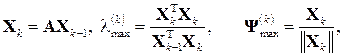 (3.8)
(3.8)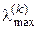 – k -те наближення максимального за модулем власного числа; Ψ
– k -те наближення максимального за модулем власного числа; Ψ 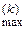 – k -те наближення відповідного власного вектора. Для початку ітераційного процесу необхідно задати початкове наближення вектора X 0.
– k -те наближення відповідного власного вектора. Для початку ітераційного процесу необхідно задати початкове наближення вектора X 0.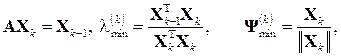
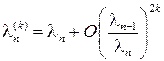 . Тому для його реалізації потрібно майже в два рази менше ітерацій, ніж для використання степеневого методу.
. Тому для його реалізації потрібно майже в два рази менше ітерацій, ніж для використання степеневого методу.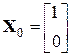 . Тоді згідно з (3.8) маємо:
. Тоді згідно з (3.8) маємо: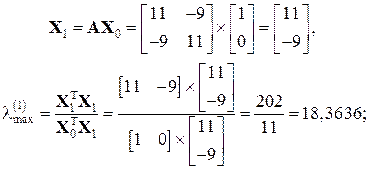
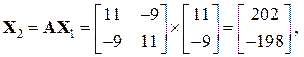
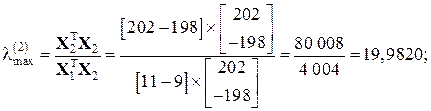
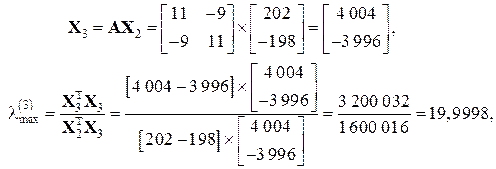
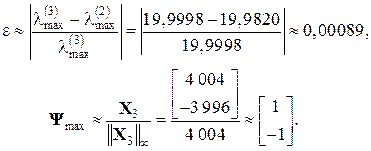
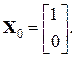 Тоді:
Тоді: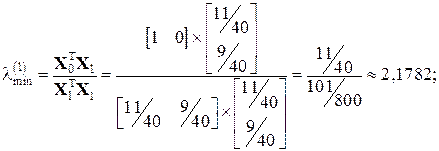 .
.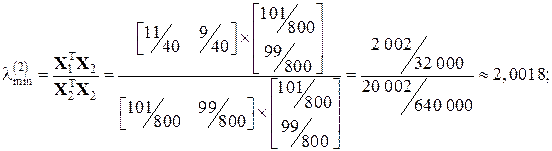
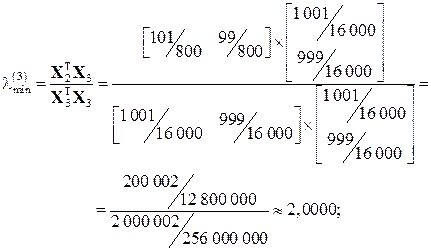
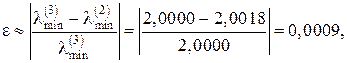
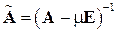 , де Е – одинична матриця. Після цього визначають максимальне за модулем власне число матриці n. Це можна зробити будь-яким відомим методом (наприклад, методом скалярних добутків). Остаточно шукане власне число l обчислюють за формулою
, де Е – одинична матриця. Після цього визначають максимальне за модулем власне число матриці n. Це можна зробити будь-яким відомим методом (наприклад, методом скалярних добутків). Остаточно шукане власне число l обчислюють за формулою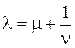 .
.