Існують два методи відокремлення коренів – це графічний та аналітичний.
Графічний метод:
Нехай потрібно відокремити корені рівняння (4.1), то потрібно побудувати графік функції  . Абсциси точок перетину цього графіка з віссю Ox і будуть наближеними значеннями коренів. Якщо рівняння (4.1) не має коренів, близьких за значенням, то краще замінити рівняння (4.1) рівносильним йому рівнянням вигляду:
. Абсциси точок перетину цього графіка з віссю Ox і будуть наближеними значеннями коренів. Якщо рівняння (4.1) не має коренів, близьких за значенням, то краще замінити рівняння (4.1) рівносильним йому рівнянням вигляду:
 , (4.2)
, (4.2)
де  і
і  - простіші функції, ніж
- простіші функції, ніж  .
.
Побудувавши графіки функції  ;
;  , одержимо наближені значення шуканих коренів, як абсциси точок перетину цих графіків.
, одержимо наближені значення шуканих коренів, як абсциси точок перетину цих графіків.
Графічний метод відокремлення коренів дозволяє грубо визначити інтервали ізоляції коренів рівняння (4.1). Для того щоб переконатися в тому, що відрізок  , знайдений графічно дійсно містить корінь і до того ж єдиний, слід скористатися властивістю неперервних функцій: якщо функція
, знайдений графічно дійсно містить корінь і до того ж єдиний, слід скористатися властивістю неперервних функцій: якщо функція  неперервна і монотонна на відрізку
неперервна і монотонна на відрізку  та на його кінцях має різні знаки
та на його кінцях має різні знаки  , то між точками
, то між точками  і
і  є лише один корінь нелінійного рівняння. Ознака монотонності функції
є лише один корінь нелінійного рівняння. Ознака монотонності функції  на розглянутому відрізку – умова знакосталості похідної
на розглянутому відрізку – умова знакосталості похідної  : якщо
: якщо  - функція
- функція  зростає, якщо
зростає, якщо  - спадає.
- спадає.
Аналітичний метод відокремлення коренів.
Ґрунтується на сформульованій вище властивості неперервних функцій та припускає такий порядок дій:
1) Знайти  - першу похідну.
- першу похідну.
2) Розв’язати рівняння  , тобто визначити корені похідної, або близьких до них значень.
, тобто визначити корені похідної, або близьких до них значень.
3) Скласти таблицю знаків функції  у межових точках області її існування, та у точках нульових значень її похідної.
у межових точках області її існування, та у точках нульових значень її похідної.
4) Виділити в таблиці знаки  інтервалів, на кінцях яких функція набуває значення протилежних знаків. У середині цих інтервалів є по одному і тільки по одному кореню (шукані інтервали).
інтервалів, на кінцях яких функція набуває значення протилежних знаків. У середині цих інтервалів є по одному і тільки по одному кореню (шукані інтервали).
Алгебричні рівняння  -го степеня
-го степеня  має не більш ніж
має не більш ніж  дійсних коренів. Тому, якщо для такого рівняння отримати
дійсних коренів. Тому, якщо для такого рівняння отримати  зміну знаків, то всі його корені відокремлені.
зміну знаків, то всі його корені відокремлені.
Наприклад: Відокремити корені рівняння  графічним та аналітичним методом
графічним та аналітичним методом  .
.
Розв’язання:
Графічний метод:
Перепишемо рівняння у вигляді  . Побудуємо графіки функцій
. Побудуємо графіки функцій  та
та  (рис.4.1). Знайдемо точки перетину цих двох графіків.
(рис.4.1). Знайдемо точки перетину цих двох графіків.
З рисунка видно, що графіки перетинаються в одній точці, яка належить інтервалу (-2;-1). Отже, рівняння  має єдиний дійсний корінь, і належить цей корінь інтервалу (-2;-1).
має єдиний дійсний корінь, і належить цей корінь інтервалу (-2;-1).

Рис. 4.1. – Графічне відокремлення коренів рівняння 
Аналітичний метод:
Позначимо  .
.
Область визначення функції  є уся числова вісь. Знайдемо першу похідну функції:
є уся числова вісь. Знайдемо першу похідну функції:  .
.
Прирівняємо цю похідну до нуля та обчислимо корені отриманого рівняння:  , звідси наближені значення коренів:
, звідси наближені значення коренів:

Складемо таблицю знаків функції  , вважаючи
, вважаючи 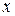 таким, що дорівнює межовим значенням області визначення функції
таким, що дорівнює межовим значенням області визначення функції  і значенням, близьким до коренів рівняння
і значенням, близьким до коренів рівняння  .
.

| 
| -3
| -2
| -1
| -0,577
|
| 0,577
|
|
|
| 
|
Знак 
|  - -
| -
| -
| +
| +
| +
| +
| +
| +
| +
| +
|
Зміна знака відбувається на проміжку (-2;-1), отже на цьому проміжку функція  має корінь.
має корінь.
Перевіримо, що на кінцях знайденого інтервалу (-2;-1) функція  набуває значень з різними знаками:
набуває значень з різними знаками:
 ;
;  .
.  ;
;  .
.
Отже, рівняння  має лише один корінь, який знаходиться на проміжку (-2;-1).
має лише один корінь, який знаходиться на проміжку (-2;-1).
Відповідь: 
Метод бісектрис
Нехай  - функція однієї дійсної змінної
- функція однієї дійсної змінної 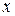 . Потрібно знайти значення кореня
. Потрібно знайти значення кореня 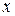 з точністю до
з точністю до  , де
, де  - додатне досить мале число.
- додатне досить мале число.
Виберемо на відрізку  яку-небудь точку
яку-небудь точку 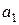 , що поділить його на два відрізки:
, що поділить його на два відрізки:  і
і  . Якщо
. Якщо  , то
, то  - корінь рівняння. Якщо
- корінь рівняння. Якщо 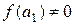 , то вибираємо з двох відрізків той, на кінцях якого функція
, то вибираємо з двох відрізків той, на кінцях якого функція  набуває значень різних знаків. Нехай це буде відрізок
набуває значень різних знаків. Нехай це буде відрізок  . У середині цього відрізка довільно виберемо точку
. У середині цього відрізка довільно виберемо точку  і повторюватимемо наші ітерації доти, доки довжина відрізка, якому належить шуканий корінь, не зменшиться чи дорівнюватиме заданій точності
і повторюватимемо наші ітерації доти, доки довжина відрізка, якому належить шуканий корінь, не зменшиться чи дорівнюватиме заданій точності  . Корінь
. Корінь 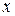 можна вважати таким, що дорівнює середньому арифметичному кінців знайденого звуженого відрізка. Похибка у цьому разі не перевищує
можна вважати таким, що дорівнює середньому арифметичному кінців знайденого звуженого відрізка. Похибка у цьому разі не перевищує  .
.
Наприклад: Метод бісектрис уточнити до 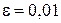 корінь рівняння
корінь рівняння 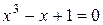 , що розташовано на проміжку
, що розташовано на проміжку  .
.
Розв’язання:
Виходячи з умов задачі, що  , позначимо
, позначимо  та
та 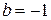 , а на кінцях відрізків функція має протилежні значення:
, а на кінцях відрізків функція має протилежні значення:  ,
,  . За точку
. За точку 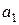 візьмемо середину відрізка
візьмемо середину відрізка  , тобто, точку
, тобто, точку  . Для зручності результати обчислення занесемо до таблиці 4.1.
. Для зручності результати обчислення занесемо до таблиці 4.1.
Таблиця 4.1

| 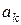
| 
| 
| 
| 
| 
| 
|
|
| -2
| -1
| -1,5
| -5
|
| -0,875<0
|
|
|
| -1,5
|  -1 -1
| -1,25
| -0,875
|
| 0,2965>0
| 0,5
|
|
|  -1,5 -1,5
| -1,25
| -1,375
| -0,875
| 0,2965
| -0,224<0
| 0,25
|
|
| -1,375
|  -1,25 -1,25
| -1,3125
| -0,224
| 0,2965
| 0,05>0
| 0,125
|
|
|  -1,375 -1,375
| -1,3125
| -1,34375
| -0,224
| 0,05
| -0,08<0
| 0,0625
|
|
|  -1,344 -1,344
| -1,3125
| -1,3282
| -0,08
| 0,05
| -0,015<0
| 0,03125
|
|
| -1,3282
|  -1,3125 -1,3125
| -1,3204
| -0,015
| 0,05
| 0,018>0
| 0,0156
|
|
| -1,3282
|  -1,3204 -1,3204
| -1,3243
| -0,015
| 0,018
| 0,0018>0
| 0,00781
|
|
|  -1,3282 -1,3282
| -1,3243
| -1,3263
| -0,015
| 0,0018
| -0,007<0
| 0,0039
|
 9 9
|  -1,3263 -1,3263
| -1,3243
| -1,3253
| -0,007
| 0,0018
| -0,0025<0
| 0,002
|
|
| -1,3253
| -1,3243
| -1,3248
| -0,0025
| 0,0018
| -0,0003<0
| 0,001
|
Із результатів таблиці видно, якщо 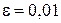 , то корінь рівняння знаходиться між точками
, то корінь рівняння знаходиться між точками  , а
, а  .
.
Відповідь:  .
.
Метод ітерацій
Нехай дано рівняння
 (4.2)
(4.2)
де  - неперервна функція. Потрібно знайти з точністю до
- неперервна функція. Потрібно знайти з точністю до  корінь
корінь 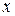 цього рівняння, відокремлений на відрізку
цього рівняння, відокремлений на відрізку  . Розв’язання такої задачі методом ітерацій починається із зведення заданого рівняння до вигляду
. Розв’язання такої задачі методом ітерацій починається із зведення заданого рівняння до вигляду
 (4.3)
(4.3)
За грубо наближене значення шуканого кореня береться будь-яка точка  , яку називають початковим наближенням. Для одержання наступного наближення
, яку називають початковим наближенням. Для одержання наступного наближення 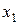 у праву частину рівняння (4.3) замість
у праву частину рівняння (4.3) замість 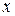 підставимо
підставимо  так що:
так що:





Таким чином, одержимо послідовність чисел  , що може збігатися, тобто мати границю, що є коренем рівняння (4.2), або розбігатися – не мати границі, тоді метод ітерацій не досягає мети.
, що може збігатися, тобто мати границю, що є коренем рівняння (4.2), або розбігатися – не мати границі, тоді метод ітерацій не досягає мети.
Взагалі, якщо  або
або  , то ітераційний процес розв’язку рівняння
, то ітераційний процес розв’язку рівняння  збігається. Якщо
збігається. Якщо  або
або  - розбігається.
- розбігається.
Для методу ітерації застосовують наступний алгоритм:
1. Перетворимо рівняння (4.2) до вигляду (4.3) так, щоб  задовольняла умову
задовольняла умову  , де
, де  - максимальне значення похідної на даному відрізку.
- максимальне значення похідної на даному відрізку.
Наприклад, можна шукати функцію  зі співвідношення
зі співвідношення  , де
, де  варто вибирати так, щоб
варто вибирати так, щоб  ;
;
 і знак
і знак  збігався б зі знаком
збігався б зі знаком  на проміжку
на проміжку  .
.
2. Обчислюємо послідовність наближення за формулою: 
 (взявши за початкове наближення
(взявши за початкове наближення  будь-яке число з відрізка
будь-яке число з відрізка  ) доти, поки для двох послідовних наближень не виконуватиметься нерівність:
) доти, поки для двох послідовних наближень не виконуватиметься нерівність:

Тоді, відповідно до формули  , одержимо
, одержимо  .
.
Наприклад: Методом ітерацій уточнити до  корінь рівняння
корінь рівняння  що розташований на відрізку
що розташований на відрізку  .
.
Розв’язання.
Зведемо дане рівняння до вигляду  .
.
Якщо подати дане рівняння у вигляді  , то
, то  ;
;  ;
;  . Умова збіжності не виконується. Тому скористаємося іншим перетворенням:
. Умова збіжності не виконується. Тому скористаємося іншим перетворенням:  ,
,  на відрізку
на відрізку  , тобто умова збіжності ітераційного процесу виконується. Тому знаходимо послідовні наближення, взявши за початкове наближення
, тобто умова збіжності ітераційного процесу виконується. Тому знаходимо послідовні наближення, взявши за початкове наближення  . Обчислення зручно подати у вигляді табл.4.2.
. Обчислення зручно подати у вигляді табл.4.2.
Таблиця 4.2.

| 
| 
| 
|
|
| -1
| -1,25992
| 0,259921
|
|
| -1,25992
| -1,31229
| 0,0523728
|
|
| -1,31229
| -1,32235
| 0,01006
|
|
| -1,32235
| -1,32427
| 0,0019149
|
|
| -1,32427
| -1,32463
| 0,0003639
|
|
| -1,32463
|
|
|
Розрахунки виконуємо за формулою:  ,
, 
Оскільки  , то потрібної точності обчислення досягнуто. Тому можна вважати, що
, то потрібної точності обчислення досягнуто. Тому можна вважати, що  .
.
Відповідь:  .
.
Метод хорд
Даний метод базується на припущенні, що на досить малому відрізку  функція
функція  змінюється лінійно. Тоді криву
змінюється лінійно. Тоді криву  на такому відрізку можна замінити хордою і за наближене значення кореня взяти точку перетину хорди з віссю
на такому відрізку можна замінити хордою і за наближене значення кореня взяти точку перетину хорди з віссю  .
.
Рівняння хорди  має вигляд:
має вигляд:

Звідси знайдемо  взявши
взявши  :
:
 (4.4)
(4.4)
Ця формула, яку називають формулою методу хорд, дає можливість обчислити наближене значення кореня.
Якщо значення 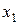 , знайдене за формулою (4.4), то наступне значення
, знайдене за формулою (4.4), то наступне значення  знаходять замінюючи
знаходять замінюючи  на
на 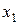 , тоді:
, тоді:
 ,
,
У загальному вигляді дана формула записується так:
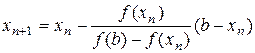 (4.5)
(4.5)
За цими формулами обчислюють корені рівняння з потрібною точністю для випадків, коли  ,
,  ,
,  ,
,  або
або  ,
,  ,
,  ,
, 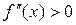 .
.
У випадках, коли  ,
,  ,
,  ,
, 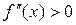 або
або  ,
,  ,
,  ,
,  , то за нерухомий кінець відрізка беруть
, то за нерухомий кінець відрізка беруть  , тобто обчислення ведеться за формулою:
, тобто обчислення ведеться за формулою:
 (4.6)
(4.6)
Наступні значення  знаходять за формулою:
знаходять за формулою:
 (4.7)
(4.7)
Абсолютну похибку наближеного значення  , якщо відомі два послідовних наближення
, якщо відомі два послідовних наближення  та
та  , оцінюють за формулою:
, оцінюють за формулою:
 , (4.8)
, (4.8)
де  ;
;  . (4.9)
. (4.9)
Якщо виконується умова  , то оцінюючи похибку наближення
, то оцінюючи похибку наближення  можна скористатися формулою:
можна скористатися формулою:
 (4.10)
(4.10)
Отже, процес обчислення послідовних наближень можна припинити, як тільки виконується нерівність
 (4.11)
(4.11)
Наприклад: Знайти корінь рівняння  методом хорд з точністю
методом хорд з точністю  на відрізку [-2;-1].
на відрізку [-2;-1].
Розв’язання.
Перевіримо, чи виконується умова (4.9) на заданому відрізку [-2;-1]:  ;
;
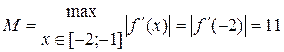 ;
;
 ;
;
 , тобто
, тобто  , тобто умова (4.9) не виконується, отже знайдемо середину заданого відрізка:
, тобто умова (4.9) не виконується, отже знайдемо середину заданого відрізка:  .
.

 при
при  умова (4.9) виконується, а це значить корінь розв’язку даного рівняння знаходиться на відрізку
умова (4.9) виконується, а це значить корінь розв’язку даного рівняння знаходиться на відрізку  . Для оцінювання похибки наближеного значення можна скористатися формулою (4.10), тобто процес послідовного наближення до кореня будемо продовжувати доти, доки не виконуватиметься умова (4.11).
. Для оцінювання похибки наближеного значення можна скористатися формулою (4.10), тобто процес послідовного наближення до кореня будемо продовжувати доти, доки не виконуватиметься умова (4.11).
Визначимо, за якою формулою варто виконувати обчислення, для чого встановимо знаки  та
та  на відрізку
на відрізку  :
:  ;
;  ;
;  ;
;  на всьому відрізку
на всьому відрізку  ,
,  ;
;  . Отже, за нерухомий кінець відрізка беремо точку
. Отже, за нерухомий кінець відрізка беремо точку  і обчислення виконуємо за формулами (4.6), (4.7). Всі обчислення занесемо у табл. 4.3.
і обчислення виконуємо за формулами (4.6), (4.7). Всі обчислення занесемо у табл. 4.3.
Таблиця 4.3.

| 
| 
| 
| 
| 
| 
| 
| 
|
|
| -1,5
| -1,0000
| -0,8750
| 1,0000
| 0,5000
| 1,8750
| -1,2667
|
|
|
| -1,5
| -1,2667
| -0,8750
| 0,2344
| 0,2333
| 1,1094
| -1,3160
| 0,0493
|
|
| -1,5
| -1,3160
| -0,8750
| 0,0370
| 0,1840
| 0,9120
| -1,3234
| 0,0075
|
|
| -1,5
| -1,3234
| -0,8750
| 0,0055
| 0,1766
| 0,8805
| -1,3245
| 0,0011
|
|
| -1,5
| -1,3245
| -0,8750
| 0,0008
| 0,1755
| 0,8758
| -1,3247
| 0,0002
|
|
| -1,5
| -1,3247
| -0,8750
| 0,0001
| 0,1753
| 0,8751
| -1,3247
| 0,0000
|
З таблиці видно, що  , тому за розв’язок рівняння беремо точку
, тому за розв’язок рівняння беремо точку  .
.
Відповідь:  .
.
Метод Ньютона
Нехай корінь 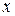 рівняння
рівняння  відокремлений на відрізку
відокремлений на відрізку  , причому
, причому  і
і  неперервні і зберігають постійні знаки, якщо
неперервні і зберігають постійні знаки, якщо  . Потрібно знайти його наближене значення з точністю до
. Потрібно знайти його наближене значення з точністю до  .
.
Запишемо рівняння прямої, дотичної до кривої  у точці х=b:
у точці х=b:
 .
.
Формула Ньютона (дотичних):
 або
або  .
.
Якщо  , то
, то  , якщо
, якщо  , то
, то  .
.
Оцінка похибки n-го наближення  :
:
 , де
, де 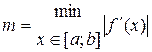 .
.
Якщо відрізок  настільки вузький, що справедлива нерівність
настільки вузький, що справедлива нерівність  , де
, де  , а
, а  , то точність наближення на
, то точність наближення на  -му кроці оцінюється в такий спосіб: якщо
-му кроці оцінюється в такий спосіб: якщо  , то
, то  .
.
Наприклад: Знайти корінь рівняння  методом Ньютона з точністю
методом Ньютона з точністю  на відрізку [-2;-1].
на відрізку [-2;-1].
Розв’язання: Визначимо, який з кінців відрізка [-2;-1] вибрати за початкове наближення.
 ;
;  ;
;  ;
;  .
.
Отже,  .
.
Результати обчислення зведемо в табл. 4.4.
Таблиця 4.4.

|
|
|
|
|
|
|

| -2,000
| -1,5455
| -1,3596
| -1,3258
| -1,3247
| -1,3247
|

| -
| 0,4545
| 0,1858
| 0,0338
| 0,0011
| 0,0000
|
З таблиці видно, що  , тому
, тому  .
.
Відповідь:  .
.
Комбінований метод
 Суть даного метода є наближення
Суть даного метода є наближення  (за методом хорд) та наближення
(за методом хорд) та наближення  (за методом Ньютона або дотичних) що підходять до кореня
(за методом Ньютона або дотичних) що підходять до кореня 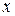 з протилежних боків відрізка
з протилежних боків відрізка  . Такий метод називається комбінованим методом хорд і дотичних.
. Такий метод називається комбінованим методом хорд і дотичних.
Якщо  та
та  дають однакові знаки, то метод хорд дає наближення кореня
дають однакові знаки, то метод хорд дає наближення кореня 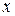 з недостачею, а метод Ньютона – з надлишком. Тоді корінь рівняння комбінованим методом обчислюється за формулами:
з недостачею, а метод Ньютона – з надлишком. Тоді корінь рівняння комбінованим методом обчислюється за формулами:
по методу хорд  ,
, 
по методу Ньютона  ,
,  (4.13)
(4.13)
У випадку, коли знаки  та
та  різні, то метод хорд дає наближення кореня
різні, то метод хорд дає наближення кореня 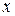 з надлишком, а метод Ньютона - з недостачею. Тоді корінь рівняння комбінованим методом обчислюється за наступними формулами:
з надлишком, а метод Ньютона - з недостачею. Тоді корінь рівняння комбінованим методом обчислюється за наступними формулами:
по методу хорд  ,
, 
по методу Ньютона  ,
,  (4.14)
(4.14)
В першому та другому випадку  ;
;  .
.
Процес обчислень можна припинити, як тільки буде виконана нерівність 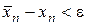 .
.
За наближене значення 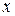 найкраще брати середнє арифметичне отриманих останніх значень
найкраще брати середнє арифметичне отриманих останніх значень  .
.
Наприклад: Знайти корінь рівняння  комбінованим методом з точністю
комбінованим методом з точністю  на відрізку [-2;-1].
на відрізку [-2;-1].
Розв’язання.
Позначимо:  ;
;  .
.
Знайдемо знаки похідних на всьому заданому відрізку:  ;
;  ;
;  ;
;  на всьому відрізку [-2;-1]. Виходячи з вищенаведеного - знаки похідних різні, тому для розрахунків комбінованим методом будемо використовувати формули (4.14):
на всьому відрізку [-2;-1]. Виходячи з вищенаведеного - знаки похідних різні, тому для розрахунків комбінованим методом будемо використовувати формули (4.14): 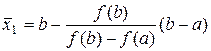 та
та  , звідси
, звідси  ,
,  . Подальші обчислення занесемо до табл. 4.5.
. Подальші обчислення занесемо до табл. 4.5.
Таблиця 4.5.

| 
| 
| 
| 
| 
| 
|

| 
| 
|
|
| -1,1667
| 0,5787
| 6,1652
| 0,3788
| 1,7244
| -1,2938
|
| -1,5455
| -1,1457
| -1,3596
|
|
| -1,29378
| 0,1282
| 4,5456
| 0,0658
| 0,2819
| -1,3237
|
| -1,3596
| -0,1537
| -1,3258
|
|
| -1,3237
| 0,0043
| 4,2732
| 0,0021
| 0,0089
| -1,3247
|
| -1,32580
| -0,0046
| -1,3247
|
З таблиці видно, що  . Отже
. Отже 
Відповідь:  .
.
Контрольні завдання
1. Вибрати з табл. 4.6 нелінійне рівняння відповідно до варіанта.
2. Визначити інтервали, що містять корені. На одному із визначених інтервалів знайти корінь рівняння методом хорд, Ньютона та комбінованим методом з похибкою, не більшою 1 %.
3. Порівняти розв’язки, знайдені різними методами.
Варіанти завдань
Таблиця 4.6. Нелінійні рівняння


 . Абсциси точок перетину цього графіка з віссю Ox і будуть наближеними значеннями коренів. Якщо рівняння (4.1) не має коренів, близьких за значенням, то краще замінити рівняння (4.1) рівносильним йому рівнянням вигляду:
. Абсциси точок перетину цього графіка з віссю Ox і будуть наближеними значеннями коренів. Якщо рівняння (4.1) не має коренів, близьких за значенням, то краще замінити рівняння (4.1) рівносильним йому рівнянням вигляду: , (4.2)
, (4.2) і
і  - простіші функції, ніж
- простіші функції, ніж  .
. ;
;  , одержимо наближені значення шуканих коренів, як абсциси точок перетину цих графіків.
, одержимо наближені значення шуканих коренів, як абсциси точок перетину цих графіків. , знайдений графічно дійсно містить корінь і до того ж єдиний, слід скористатися властивістю неперервних функцій: якщо функція
, знайдений графічно дійсно містить корінь і до того ж єдиний, слід скористатися властивістю неперервних функцій: якщо функція  неперервна і монотонна на відрізку
неперервна і монотонна на відрізку  , то між точками
, то між точками  і
і  є лише один корінь нелінійного рівняння. Ознака монотонності функції
є лише один корінь нелінійного рівняння. Ознака монотонності функції  - функція
- функція  - спадає.
- спадає. - першу похідну.
- першу похідну. , тобто визначити корені похідної, або близьких до них значень.
, тобто визначити корені похідної, або близьких до них значень. у межових точках області її існування, та у точках нульових значень її похідної.
у межових точках області її існування, та у точках нульових значень її похідної. -го степеня
-го степеня  має не більш ніж
має не більш ніж  зміну знаків, то всі його корені відокремлені.
зміну знаків, то всі його корені відокремлені. .
. . Побудуємо графіки функцій
. Побудуємо графіки функцій  та
та  (рис.4.1). Знайдемо точки перетину цих двох графіків.
(рис.4.1). Знайдемо точки перетину цих двох графіків. має єдиний дійсний корінь, і належить цей корінь інтервалу (-2;-1).
має єдиний дійсний корінь, і належить цей корінь інтервалу (-2;-1).
 .
. .
. , звідси наближені значення коренів:
, звідси наближені значення коренів:
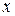 таким, що дорівнює межовим значенням області визначення функції
таким, що дорівнює межовим значенням області визначення функції 



 -
-
 ;
;  .
.  ;
;  .
. має лише один корінь, який знаходиться на проміжку (-2;-1).
має лише один корінь, який знаходиться на проміжку (-2;-1).
 , де
, де  яку-небудь точку
яку-небудь точку 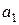 , що поділить його на два відрізки:
, що поділить його на два відрізки:  і
і  . Якщо
. Якщо  , то
, то  - корінь рівняння. Якщо
- корінь рівняння. Якщо 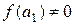 , то вибираємо з двох відрізків той, на кінцях якого функція
, то вибираємо з двох відрізків той, на кінцях якого функція  і повторюватимемо наші ітерації доти, доки довжина відрізка, якому належить шуканий корінь, не зменшиться чи дорівнюватиме заданій точності
і повторюватимемо наші ітерації доти, доки довжина відрізка, якому належить шуканий корінь, не зменшиться чи дорівнюватиме заданій точності  .
.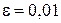 корінь рівняння
корінь рівняння 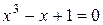 , що розташовано на проміжку
, що розташовано на проміжку  .
. , позначимо
, позначимо  та
та 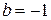 , а на кінцях відрізків функція має протилежні значення:
, а на кінцях відрізків функція має протилежні значення:  ,
,  . За точку
. За точку  , тобто, точку
, тобто, точку  . Для зручності результати обчислення занесемо до таблиці 4.1.
. Для зручності результати обчислення занесемо до таблиці 4.1.
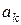






 -1
-1
 -1,5
-1,5
 -1,25
-1,25
 -1,375
-1,375
 -1,3125
-1,3125
 9
9
 -1,3263
-1,3263
 , а
, а  .
. (4.2)
(4.2) . Розв’язання такої задачі методом ітерацій починається із зведення заданого рівняння до вигляду
. Розв’язання такої задачі методом ітерацій починається із зведення заданого рівняння до вигляду (4.3)
(4.3) , яку називають початковим наближенням. Для одержання наступного наближення
, яку називають початковим наближенням. Для одержання наступного наближення 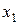 у праву частину рівняння (4.3) замість
у праву частину рівняння (4.3) замість  так що:
так що:




 , що може збігатися, тобто мати границю, що є коренем рівняння (4.2), або розбігатися – не мати границі, тоді метод ітерацій не досягає мети.
, що може збігатися, тобто мати границю, що є коренем рівняння (4.2), або розбігатися – не мати границі, тоді метод ітерацій не досягає мети. або
або  , то ітераційний процес розв’язку рівняння
, то ітераційний процес розв’язку рівняння  або
або  - розбігається.
- розбігається. задовольняла умову
задовольняла умову  , де
, де  - максимальне значення похідної на даному відрізку.
- максимальне значення похідної на даному відрізку. зі співвідношення
зі співвідношення  , де
, де  ;
; і знак
і знак  .
. (взявши за початкове наближення
(взявши за початкове наближення  будь-яке число з відрізка
будь-яке число з відрізка 
 , одержимо
, одержимо  .
. корінь рівняння
корінь рівняння  що розташований на відрізку
що розташований на відрізку  , то
, то  ;
;  ;
;  . Умова збіжності не виконується. Тому скористаємося іншим перетворенням:
. Умова збіжності не виконується. Тому скористаємося іншим перетворенням:  ,
,  на відрізку
на відрізку  . Обчислення зручно подати у вигляді табл.4.2.
. Обчислення зручно подати у вигляді табл.4.2.


 ,
, 
 , то потрібної точності обчислення досягнуто. Тому можна вважати, що
, то потрібної точності обчислення досягнуто. Тому можна вважати, що  .
. .
. .
. має вигляд:
має вигляд:
 взявши
взявши  :
: (4.4)
(4.4) знаходять замінюючи
знаходять замінюючи  ,
,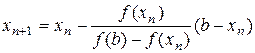 (4.5)
(4.5) ,
,  ,
,  ,
,  або
або  ,
,  ,
,  ,
, 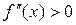 .
. , тобто обчислення ведеться за формулою:
, тобто обчислення ведеться за формулою: (4.6)
(4.6) знаходять за формулою:
знаходять за формулою: (4.7)
(4.7) та
та  , (4.8)
, (4.8) ;
;  . (4.9)
. (4.9) , то оцінюючи похибку наближення
, то оцінюючи похибку наближення  (4.10)
(4.10) (4.11)
(4.11) на відрізку [-2;-1].
на відрізку [-2;-1]. ;
;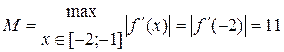 ;
; ;
; , тобто
, тобто  , тобто умова (4.9) не виконується, отже знайдемо середину заданого відрізка:
, тобто умова (4.9) не виконується, отже знайдемо середину заданого відрізка:  .
.
 при
при  умова (4.9) виконується, а це значить корінь розв’язку даного рівняння знаходиться на відрізку
умова (4.9) виконується, а це значить корінь розв’язку даного рівняння знаходиться на відрізку  на відрізку
на відрізку  ;
;  ;
;  ;
;  . Отже, за нерухомий кінець відрізка беремо точку
. Отже, за нерухомий кінець відрізка беремо точку  і обчислення виконуємо за формулами (4.6), (4.7). Всі обчислення занесемо у табл. 4.3.
і обчислення виконуємо за формулами (4.6), (4.7). Всі обчислення занесемо у табл. 4.3.



 , тому за розв’язок рівняння беремо точку
, тому за розв’язок рівняння беремо точку  .
. .
. . Потрібно знайти його наближене значення з точністю до
. Потрібно знайти його наближене значення з точністю до  .
. або
або  .
. , то
, то  , якщо
, якщо  , то
, то  .
. , де
, де 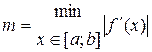 .
. , де
, де  , а
, а  , то точність наближення на
, то точність наближення на  , то
, то  .
. ;
;  ;
;  .
. .
.


 , тому
, тому  .
. (за методом Ньютона або дотичних) що підходять до кореня
(за методом Ньютона або дотичних) що підходять до кореня  ,
, 
 ,
,  ,
,  ,
,  .
.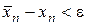 .
. .
. ;
;  ;
; 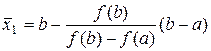 та
та  , звідси
, звідси  ,
,  . Подальші обчислення занесемо до табл. 4.5.
. Подальші обчислення занесемо до табл. 4.5.








 . Отже
. Отже 



