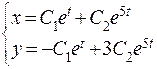Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Линейные однородные дифференциальные уравнения высших порядков (ЛОДУ).Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Определение. Дифференциальное уравнение вида:
называется линейным дифференциальным уравнением n-ого порядка. Если Пусть
СВОЙСТВА ЛОДУ. ТЕОРЕМА 5.1 Пусть Доказательство: вытекает из первого свойства линейного дифференциального оператора.
ТЕОРЕМА 5.2 Пусть Доказательство: вытекает из второго свойства линейного дифференциального оператора.
Следствие: Пусть Определение. Любые ТЕОРЕМА 6.3 Общее решение ЛОДУ (5.2) Замечание. Таким образом общее решение ЛОДУ является линейной комбинацией его ФСР. Как вытекает из этих результатов, множество всех решений ЛОДУ образует Замечание. максимальное количество линейно независимых решений ЛОДУ
§ 7. ЛОДУ с постоянными коэффициентами
Рассмотрим Найдем вид общего решения в различных случаях
Решения
Все корни различны и действительны Имеем n различных корней характеристического уравнения (7.2), им соответствует n корней
Пример 1 Решение. характеристическое уравнение имеет вид:
Все корни различны, среди них есть комплексные Комплексные корни уравнения (7.2) являются сопряженными вида Пример 2 Решение. Характеристическое уравнение имеет вид: Тогда общее решение имеет вид:
Имеются кратные корни В 2-ч предыдущих случаях найденное число линейно независимых решений равнялось В настоящем случае число различных корней характеристического уравнения Пусть Докажем это. Рассмотрим 2 случая: 1) Запишем соответствующе дифференциальное уравнение
Решение этого уравнения: Тогда дополнительное решение действительно имеет вид 2) Такая замена не нарушает линейности и однородности уравнения (7.1) После подстановки получившихся выражений имеем: Корни (7.4) отличаются от корней (7.2) на Заметим, что кратные комплексные сопряженные корни дают решение вида:
Пример 3 Решение. Характеристическое уравнение имеет вид: Пример 4 Решение. Характеристическое уравнение имеет вид: Тогда по схеме 3-го случая общее решение имеет вид:
§10 Система линейных ДУ с постоянными коэффициентами.
Определение. Система дифференциальных уравнений называется линейной, если она линейна относительно всех неизвестных функций и их производных. Определение. Линейная система дифференциальных уравнений 1-го порядка Обозначим: Тогда (1) можно записать в матричной форме Определение. Векторы Если из выполняющегося равенства 3 на всем отрезке Из свойств линейного оператора следует, что решение однородной линейной системы имеют те же свойства, то есть их линейная комбинация является также решением однородной системы. Отсюда вытекает (с учетом определения линейной независимости) следующая теорема.
ТЕОРЕМА 10.1 Общим решением линейной однородной системы дифференциальных уравнений (4) Доказательство.
Уравнение (6) называется характеристическим Найдя корни характеристического уравнения (оно Это только в случае различных корней.
Пример 1 Решение. Составим характеристическое уравнение
Возьмем
Пример 1 Решение. Составим характеристическое уравнение
Возьмем
|
||
|
Последнее изменение этой страницы: 2017-02-05; просмотров: 1228; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.57 (0.007 с.) |

 (5.1)
(5.1)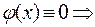 линейное однородное дифференциальное уравнение n-ого порядка.
линейное однородное дифференциальное уравнение n-ого порядка. , тогда на
, тогда на  ЛОДУ n -ого порядка
ЛОДУ n -ого порядка (5.2)
(5.2) (5.2a)
(5.2a) (*)
(*) является решением ЛОДУ (5.2). Тогда
является решением ЛОДУ (5.2). Тогда  также является решением (5.2).
также является решением (5.2). и
и  являются решением ЛОДУ (5.2). Тогда
являются решением ЛОДУ (5.2). Тогда  также является решением.
также является решением. решение ЛОДУ (5.2). Тогда их линейная комбинация
решение ЛОДУ (5.2). Тогда их линейная комбинация  также является решением ЛОДУ (5.2).
также является решением ЛОДУ (5.2). линейных независимых решений ЛОДУ
линейных независимых решений ЛОДУ  го порядка называются его фундаментальной системой решений (ФСР).
го порядка называются его фундаментальной системой решений (ФСР).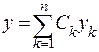 (6.3), где
(6.3), где  - линейно независимые решения (5.2), а
- линейно независимые решения (5.2), а  -постоянный коэффициент
-постоянный коэффициент мерное линейное пространство для которого любая ФСР является базисом.
мерное линейное пространство для которого любая ФСР является базисом.
 (7.1)
(7.1) -постоянных
-постоянных - является частным решением уравнения (7.1)
- является частным решением уравнения (7.1)
 -характеристическое уравнение для (7.1)-(7.2)
-характеристическое уравнение для (7.1)-(7.2) характеристического уравнения при подстановке в
характеристического уравнения при подстановке в  дают частные решения уравнения (7.1), причем все. Общее решение по теореме 6.3 является линейной комбинацией этих частных решений. Таким образом, мы свели задачу решения ЛОДУ с постоянными коэффициентами к задаче нахождения корней алгебраического уравнения степени n.
дают частные решения уравнения (7.1), причем все. Общее решение по теореме 6.3 является линейной комбинацией этих частных решений. Таким образом, мы свели задачу решения ЛОДУ с постоянными коэффициентами к задаче нахождения корней алгебраического уравнения степени n. . Согласно примеру 6.2 эти функции линейно независимы, следовательно образуют ФСР ЛОДУ (7.1), следовательно по теореме 6.3 общее решение (7.1)
. Согласно примеру 6.2 эти функции линейно независимы, следовательно образуют ФСР ЛОДУ (7.1), следовательно по теореме 6.3 общее решение (7.1) .
.


 - общее решение уравнения
- общее решение уравнения им соответствуют корни (7.1) вида
им соответствуют корни (7.1) вида  тогда подставляя решение этого вида в (7.1) выделяя действительные и мнимые части и приравнивая их к нулю, находим, что указанной паре комплексных корней соответствует решение (7.1) вида:
тогда подставляя решение этого вида в (7.1) выделяя действительные и мнимые части и приравнивая их к нулю, находим, что указанной паре комплексных корней соответствует решение (7.1) вида:  и
и 




 порядку уравнения (7.1), то есть было максимальным, поэтому решения образовывали ФСР.
порядку уравнения (7.1), то есть было максимальным, поэтому решения образовывали ФСР. . Для получения общего решения найдем дополнительное решение другого вида.
. Для получения общего решения найдем дополнительное решение другого вида. – корень характеристического уравнения (7.2) кратности
– корень характеристического уравнения (7.2) кратности  . Тогда дополнительное решение имеет вид:
. Тогда дополнительное решение имеет вид: 
 (корень кратности
(корень кратности 

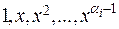
 (*)
(*) (корень кратности
(корень кратности 
 коэффициенты
коэффициенты  по-прежнему постоянные. Выпишем характеристическое уравнение для (7.3):
по-прежнему постоянные. Выпишем характеристическое уравнение для (7.3):  (7.4)
(7.4) , так как при
, так как при 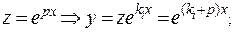
 . Тогда этот случай сводится к предыдущему, так как корень характеристического уравнения
. Тогда этот случай сводится к предыдущему, так как корень характеристического уравнения  (корень кратности
(корень кратности  ). Соответствующие решения
). Соответствующие решения  вида
вида 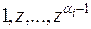 . Делая обратную замену, получаем (*) Таким образом каждому кратному корню соответствует столько дополнительных корней, какова его кратность, итоговое число линейно независимых решений (7.1) равно числу корней характеристического уравнения (7.2) с учетом их кратности.
. Делая обратную замену, получаем (*) Таким образом каждому кратному корню соответствует столько дополнительных корней, какова его кратность, итоговое число линейно независимых решений (7.1) равно числу корней характеристического уравнения (7.2) с учетом их кратности.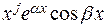 и
и 

 – корень кратности 2 Общее решение имеет вид:
– корень кратности 2 Общее решение имеет вид: 



 (1)
(1)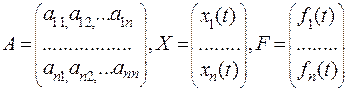
 . Обозначим линейный оператор
. Обозначим линейный оператор  .По свойствам линейного оператора получаем:1)
.По свойствам линейного оператора получаем:1) 

 где
где  называются линейно зависимыми на
называются линейно зависимыми на  , если найдутся
, если найдутся  , не обращающиеся одновременно в ноль, такие, что:
, не обращающиеся одновременно в ноль, такие, что:  при всех
при всех 
 , то эти векторы называются линейно независимыми.
, то эти векторы называются линейно независимыми. является линейная комбинация линейных независимых решений этой системы:
является линейная комбинация линейных независимых решений этой системы: 
 (6)
(6) – степени и потому имеет, с учетом кратности,
– степени и потому имеет, с учетом кратности, 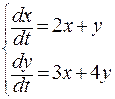


 ,
, 
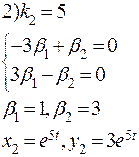 Общее решение имеет вид:
Общее решение имеет вид: