
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Оценка привилегированной акцииСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Стоимость привилегированной акции – текущая стоимость в денежном выражении серий равных периодических потоков денежных средств (дивидендов), имеющих место без ограничения во времени. Поскольку для привилегированных акций дивиденды для каждого временного периода остаются неизменными, модель оценки имеет следующий вид:
где V – текущая стоимость привилегированной акции; D – годовой дивиденд; r – требуемая ставка дохода инвестора. Для расчета ожидаемой нормы прибыли держателя привилегированной акции мы используем уравнение определения стоимости привилегированной акции, представленное в примере. Решая его для r, получаем:
из чего видно, что ожидаемая норма прибыли для привилегированной акции равна дивидендному доходу (годовой дивиденд / рыночная цена).
Оценка обыкновенной акции
Стоимость обыкновенной акции представляет собой текущую стоимость всех будущих притоков денежных средств, ожидаемых инвестором, включая дивиденды и будущую стоимость акции на дату ее продажи. Разовый период владения Для инвестора, владеющего обыкновенной акцией в течение только одного года, стоимость акции представляет собой текущую стоимость как ожидаемых денежных дивидендов, которые должны быть получены за один год (D1), так и ожидаемую рыночную стоимость акции на конец года (Р1). Если (r) представляет требуемую ставку дохода инвестора, стоимость обыкновенной акции (Р0) составляет:
Расчет ожидаемой нормы прибыли (ставки доходности) на обыкновенную акцию получим из формулы (6:
или:
Многократный период владения Поскольку обыкновенная акция не имеет срока погашения и ею можно владеть многие годы, необходима более общая, многопериодная модель для расчета ее стоимости. Модель оценки обыкновенной акции:
где Dt – дивиденд за период t от 1 до n лет. Дивиденды могут быть разделены по категориям: дивиденды с нулевым ростом и дивиденды с постоянным ростом. В случае нулевого роста (то есть D0 = D1 =...= D) модель оценки стоимости акции будет.
Данная модель наиболее применима для оценки привилегированных акций или обыкновенных акций очень солидных компаний. В случае постоянного роста, если мы предположим, что дивиденды растут с постоянным темпом g ежегодно
тогда общая модель оценки акции будет иметь вид:
Формулу можно представить как:
Эта формула, известная как модель оценки Гордона, является наиболее применимой при оценке обыкновенных акций очень крупных или многоотраслевых компаний. Ожидаемую норму прибыли держателя обыкновенной акции с темпом роста g получим из формулы:
Задания: 1. Рассчитать наращенную сумму с исходной суммы в 1 тыс. руб. при размещении ее в банке на условиях начисления простых и сложных процентов, если: а) годовая ставка 20 %; б) периоды наращения 90 дней, 180 дней, 1 год, 5 лет, 10 лет (если считать, что в году 360 дней). 2. Векселедержатель предъявил для учета вексель на сумму 50 тыс. руб. со сроком погашения 28.09.97 г. Вексель предъявлен 13.09.97 г. Банк согласился учесть вексель по учетной ставке 30 % годовых. Определить сумму, которую векселедержатель получит от банка. 3. Приведены данные о денежных потоках:
Требуется рассчитать для каждого потока показатели FV при r=12 % и PV при r=15 % для двух случаев: а) потоки имеют место в начале года; б) потоки имеют место в конце года. 4. Оцените текущую стоимость облигации номиналом в 1000 $, купонной ставкой 9 % годовых и сроком погашения через 3 года, если рыночная норма прибыли равна 7 %. 5. Ценная бумага через 5 лет начнет генерировать бессрочный денежный поток в размере 1000 $ в год. По какой цене можно купить эту бумагу сегодня, если применяемая норма прибыли равна 12 %? 6. На рынке продаются две бескупонные облигации: облигация В1 номиналом 10000 руб. и сроком погашения через три года продается за 8 тыс. руб.; облигация В2 номиналом в 10000 руб. и сроком погашения через 10 лет продается за 4,5 тыс. руб. Какая облигация более выгодная для инвестирования? 7. Рыночная цена акции за год понизилась с 25 до 20 $. Рассчитайте показатели общей, капитализированной и дивидендной доходности, если выплаченный дивиденд составил: а) 3$; б) 5$; в) 8 $. 8. Клиент в конце каждого года вкладывает 3 тыс. руб. в банк, выплачивающий сложные проценты по процентной ставке 25 % годовых. Определите сумму, которая будет на счете клиента через 7 лет. Если эта сумма получается в результате однократного помещения денег в банк в начале первого года, то какой величины должен быть взнос? Как изменятся найденные величины, если деньги вкладываются в начале каждого года?
9. Ежегодно в начале года в банк делается очередной взнос в размере 14 тыс. руб. Банк устанавливает годовую номинальную процентную ставку 36 %. Какая сумма будет на счете по истечении шести лет, если начисление сложных процентов происходит: а) ежегодно; б) ежеквартально; в) ежемесячно. 10. Имеется переменный аннуитет постнумерандо (тыс. руб.): 20, 12, 8, 45, 30. Рассчитайте: а) будущую стоимость аннуитета; б) приведенную стоимость аннуитета, если его период совпадает с базовым периодом начисления процентов по сложной процентной ставке 25 % годовых, т.е. равен одному году. Как изменятся полученные оценки, если исходный поток представляет собой аннуитет пренумерандо? 11. За пять лет необходимо накопить 40 тыс. руб. Какой величины должен быть первый вклад, если предполагается каждый год увеличивать величину денежного поступления на 15 % и процентная ставка равна 24 % годовых? Денежные поступления и начисления сложных процентов осуществляются в конце года. 12. Имеется ценная бумага, которая по истечении трех лет даст право на получение дохода в размере 800 тыс. руб. Текущая стоимость денег на рынке капитала равна 15% в год. Рассчитать текущую стоимость ценной бумаги. 13. Предполагается, что акция будет приносить ежегодные дивиденды в сумме 45 рублей в течение 5 лет. Средняя ставка доходности прогнозируется так: 20%, 20%, 20%, 15%, 13% годовых. Определите настоящую приведенную стоимость денежных поступлений. 14. Предполагается, что акция будет приносить ежегодные дивиденды в размере 25, 25, 30, 30 рублей соответственно в течение 4-х лет. При этом средняя доходность финансового рынка будет принимать значения 20 %, 25 %, 25 %, 30 %. Определите настоящую приведенную стоимость будущих дивидендов. 15. Дивиденды на акцию составят за первый год 50 рублей, а затем будут постоянно увеличиваться с темпом прироста 0,1. Найдите настоящую приведенную стоимость будущих поступлений средств, использую в качестве ставки дисконта ставку 20 %. 16. Прогнозируется, что дивиденды по обыкновенной акции составят в первый год 40 рублей, затем в течение 3-х лет будут увеличиваться с темпом прироста 0,1, а в течение последующих 2-х лет с темпом прироста 0,15. Считать ставку доходности равной 20 %. Определите приведенную стоимость будущих дивидендов. 17. Дивиденды по обыкновенной акции за первый год составят 75 рублей. Затем 2 года будет прирост с темпом 0,2, а затем установится постоянный темп прироста 0,1. Определите: а) настоящую стоимость денежного потока; б) стоимость денежного потока на конец третьего года. 18. Инвестору предлагают приобрести за 75 тысяч рублей облигацию с нулевым купоном номиналом 120 тысяч рублей и сроком обращения 4 года. Стоит ли совершать покупку, если на протяжении этих 4-х лет существует возможность вложения средств под 7 % годовых? 19. На рынке обращаются облигации номиналом 150 тысяч рублей и с купонным доходом 6,3 % годовых. До погашения облигаций осталось 5 лет, а рыночная цена на настоящий момент составляет 107 тысяч рублей. Определите доходность к погашению. 20. Доходность к погашению выпускаемых облигации номиналом 250 тысяч рублей составляет 13 %. Облигации выпускаются на 6 лет с условием ежегодных выплат процентного
Тесты: 1. Доход от вложений денежных средств при начислении его методом простого процента: а) выше, чем при применении сложного процента; б) ниже; в) одинаков.
2. Эффективная ставка процента - это: а) процентное отношение дохода на капитал в конце года к величине капитала в начале года; б) ставка для начисления процентов в каждом отдельном периоде года; в) ставка, равная произведению ставки каждого отдельного периода на количество периодов начисления процентов в течение года. 3. Годовая номинальная ставка - это: а) процентное отношение дохода на капитал в конце года к величине капитала в начале года; б) ставка, равная произведению ставки каждого отдельного периода на количество периодов начисления процентов в течение года; в) ставка для начисления процентов в каждом отдельном периоде года.
4. Аннуитет - это: а) вложение в ценные бумаги; б) единовременный вклад в банк; в) серия равновеликих платежей в течение определенного количества периодов.
5. Будущая стоимость авансового аннуитета: а) выше будущей стоимости обычного аннуитета; б) ниже ее; в) равна ей.
6. Текущая стоимость будущего капитала рассчитывается методом: а) дисконтирования; б) начисления процентов.
7. Будущая стоимость текущего капитала рассчитывается методом: а) дисконтирования; б) начисления процентов.
8. Дисконтирование - это: а) приведение будущей стоимости к современной величине; б) приведение текущей стоимости к будущей величине. в) учет инфляции.
9. Метод аннуитета применяется при расчете 1) равных сумм платежей за ряд неодинаковых периодов; 2) неравных сумм платежей за ряд неодинаковых периодов; 3) равных сумм платежей за ряд одинаковых периодов; 4) неравных сумм платежей за ряд одинаковых периодов; 5) остатка долга по кредиту.
|
||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2017-02-05; просмотров: 823; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.191.255.180 (0.01 с.) |

 ,
,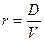 ,
,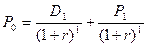 ,
, ,
,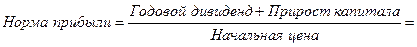

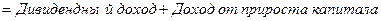
 ,
, ,
,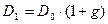 ,
,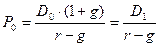 ,
,
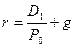
 дохода в размере 20 тысяч рублей. Оцените настоящую приведенную стоимость облигации.
дохода в размере 20 тысяч рублей. Оцените настоящую приведенную стоимость облигации.


