Дифракция, условие её наблюдения. Принцип гюйгенса-френеля. Метод зон Френеля и его применение для расчета дифракции света на узкой щели.

Дифракция – нарушение прямолинейности распространения и попадания волны в область геометрической тени. Дифракция свойственна волнам любой природы.

В естественных условиях дифракция наблюдается в виде нерезкой, размытой границы тени предмета. Подробное изучение показывает, что причиной нерезкости являются узкие интерференционные полосы вблизи границы геометрической тени. Вследствие дифракции оптическая система (например, микроскоп) изображает точку в монохроматическом свете в виде светлого пятна, окруженного попеременно темными и светлыми кольцами, поэтому разрешающая способность оптических приборов ограничена.

Принцип Гюйгенса-Френеля:

1. Каждая точка фронта волны является вторичным источником, от которого распространяется вперед полусферическая волна.

Новое положение фронта волны есть огибающее фронтов вторичных волн.

2. Вторичные источники когерентны, интерферируя между собой, они дают максимумы и минимумы интенсивности в дифракционной картине.

Зоны Френеля:

Распределение на эк­ране интенсивности дифрагировавшего излуче­ния можно рассчитать, пользуясь принципом Гюйгенса-Френеля, со­гласно которому фронт волны может рассматри­ваться как совокупность когерентных точечных источников. Пришедшие на экран волны, испу­щенные этими источни­ками, интерферируют между собой.

Рассмотрим распространение монохроматической световой волны от точечного источника S в некоторую точку Р на экране (рис. 1.4).

Согласно принципу Гюйгенса-Френеля действие источника S заменим действием воображаемых когерентных источников. Они располагаются на поверхности фронта волны, представляющей собой в некоторый момент времени сферу радиусом а, пересе­кающуюся в точке О с прямой SP.

На рис. 1.4 фронт волны изобразится дугой радиусом а с цен­тром в S. Далее поверхность фронта разобьем на кольцевые об­ласти, расстояния от краев которых до точки Р отличаются на λ/2. Эти области называются зонами Френеля. Пронумеруем их, начиная с ближайшей к точке Р, как показано на рис. 1.4. Расчет показывает, что площади всех зон Френеля одинаковы, т.е. каж­дая из них содержит одно и то же число точечных источников, излучающих одинаковую энергию. Радиус зоны Френеля с номе­ром т выражается формулой

Волновой процесс в точке Р можно рассматривать как резуль­тат интерференции волн, приходящих от каждой зоны в отдель­ности. Волны из соседних зон приходят в противофазе и ослаб­ляют друг друга. Поэтому, если между источником S и экраном поставить преграду, оставляющую открытыми четное число зон Френеля, то свет в точку Р не попадет. При нечетном числе зон Френеля одна из зон окажется непогашенной и в точке Р будет наблюдаться светлое пятно.

В случае плоской волны при а → ∞ согласно предыдущей формуле получим выражение для радиуса зоны Френеля:

Дифракция на щели:

Метод зон Френе­ля позволяет рассчи­тать дифракцию пло­ской световой волны на щели шириной b. Схема хода лучей по­казана на рис. 1.5. Лучи, идущие под углом φ, линза соби­рает в точке М.

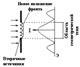
При условии

щель содержит четное число зон Френеля и в точке М будет ми­нимум интенсивности.