
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Гармонический осциллятор, его Закон движения, скорость, ускорение, возвращающая сила, энергия.Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Гармонический осциллятор, его закон движения, скорость, ускорение, возвращающая сила, энергия. Гармонический осциллятор – система, совершающая колебания, описываемые дифференциальным уравнением гармонических колебаний: За период колебаний фаза колебания получает приращение 2 π, т.е.: Запишем первую и вторую производные по времени от гармонически колеблющейся величины s:
Из последнего выражения и следует дифференциальное уравнение гармонических колебаний Пусть материальная точка совершает прямолинейные гармонические колебания вдоль оси координат х около положения равновесия, принятого за начало координат. Тогда зависимость координаты х от времени t задается уравнением, аналогичным уравнению (*), где s = x: Скорость и ускорение – это первая и вторая соответственно производные от х:
Сила F = ma, действующая на колеблющуюся м.т. массой m вышенаписанных уравнений, равна:
Кинетическая энерги я Потенциальная энергия Полная энергия Е: ВЫВОДЫ: 1. Колебания возникают при условии: а) положения равновесия Если уравнение движения имеет такой вид, то это гармонические колебания с Примерами гармонического осциллятора являются пружинный, физический и математический маятники, колебательный контур.
Резонанс. Анализ зависимости А=A(ω) амплитуды от частоты вынужд. силы показывает, что система по разному откликается на внешнее воздействие и при определенной частоте этот отклик наибольший и амплитуда максимальная. Такое явление называется резонансом. Частота, при которой он наступает, называется резонансной ωр. ωр -?
δ – коэффициент затухания:
Ар→∞ при δ →0 Резонансные кривые показаны на рисунке.
Кольца Ньютона
Разность хода этих лучей: Радиусы светлых колец в отраженном свете (или темных в проходящем): радиусы темных колец в отраженном свете (или светлых в проходящем): Полосы равного наклона (интерференция от плоскопараллельной пластинки)
Лучи 1' и 1 ", отразившиеся от верхней и нижней граней пластинки (рис.250), параллельны друг другу, так как пластинка плоскопараллельна. Следовательно, интерферирующие лучи 1 ' и 1 " «пересекаются» только в бесконечности, поэтому говорят, что полосы равного наклона локализованы в бесконечности. Для их наблюдения используют собирающую линзу и экран (Э), расположенный в фокальной плоскости линзы. Параллельные лучи 1' и 1" соберутся в фокусе F линзы (на рис. 250 ее оптическая ось параллельна лучам 1' и 1"), в эту же точку придут и другие лучи (на рис.250 — луч 2), параллельные лучу 1, в результате чего увеличивается общая интенсивность. Лучи 3, наклоненные под другим углом, соберутся в другой точке Р фокальной плоскости линзы. Легко показать, что если оптическая ось линзы перпендикулярна поверхности пластинки, то полосы равного наклона будут иметь вид концентрических колец с центром в фокусе линзы. Применение интерференции света Явление интерференции обусловлено волновой природой света; его количественные закономерности зависят от длины волны l0.Поэтому это явление применяется для подтверждения волновой природы света и для измерения длин волн (интерференционная спектроскопия). Явление интерференции применяется также для улучшения качества оптических приборов (просветление оптики) и получения высокоотражающих покрытий.
хода — равна (2m+1)l0/2. Явление интерференции также применяется в очень точных измерительных приборах, называемых интерферометрами. Все интерферометры основаны на одном и том же принципе и различаются лишь конструкционно. Интерферометры — очень чувствительные оптические приборы, позволяющие определять незначительные изменения показателя преломления прозрачных тел (газов, жидких и твердых тел) в зависимости от давления, температуры, примесей и т. д.
Поляризация света. Поляризатор и анализатор. Закон Малюса. Примеры получения и применения поляризованного света. Свет:
Волна называется поляризованной, если плоскость, в которой колеблется
Ест. свет = поляриз.
Устройство, превращающее естественный свет в поляризованный называется поляризатором. Он пропускает колебания только определенного направления (например, пропускает колебания, параллельные главной плоскости поляризатора, и полностью задерживает перпендикулярные этой плоскости. Устройство, служащее для анализа степени поляризации света, называется анализатором. Оба устройства совершенно одинаковы (их можно поменять местами). Схема классического опыта с турмалином:
Закон Малюса:
Примеры получения и применения поляризованного света: 1. Закон Брюстера: При отражении от диэлектрика происходит частичная или полная поляризация естественного света.
Если 2. Двойное лучепреломление: Проходя через прозрачный анизотропный кристалл, под углом к его оптической оси естественный свет делится на два луча.
3. Дихроизм. 4. Применение поляризованного света: а) метод фотоупругости; б) вращение плоскости поляризации: оптически активные вещества (кварц, раствор сахара). φ ~ d – твердые тела; φ ~ d c – жидкости, где d – толщина, с - концентрация, φ – угол поворота плоскости поляризации. Законы излучения абсолютно черного тела: Закон Стефана-Больцмана, закон Вина. Трудности классической физики при объяснении распределения энергии в спектре черного тела. Квантовая гипотеза Планка. 1. Закон Стефана-Больцмана: Для а.ч.т.: Для серого тела: Закон Стефана — Больцмана, определяя зависимость RT от температуры, не дает ответа относительно спектрального состава излучения черного тела. Из экспериментальных кривых зависимости функции rl,T (r l,T =(c/l 2 )rv,T) от длины волны l при различных температурах (рис.) следует, что распределение энергии в спектре черного тела является неравномерным. Все кривые имеют явно выраженный максимум, который по мере повышения температуры смещается в сторону более коротких волн. 2. Закон Вина:
Попытки объяснить распределение энергии в спектре черного тела с помощью волновой теории оказались неудачными. Несмотря на то что законы Стефана — Больцмана и Вина играют, в теории теплового излучения важную роль, они являются частными законами, так как не дают общей картины распределения энергии по частотам при различных температурах. Согласно теории относительности Эйнштейна энергия W и масса m взаимосвязаны: W=mc2, где с = 3 * 108 м/с – скорость света в вакууме. При излучении энергии масса тела уменьшается, при поглощении – увеличивается. Квантовая гипотеза. Формула Планка: При объяснении законов теплового излучения возникла гипотеза о квантах, с которой началась квантовая физика: электромагнитное излучение испускается порциями (квантами) с энергией Согласно электромагнитной теории в замкнутом объеме (резонаторе) существуют устойчиво только колебания, соответствующие стоячим волнам.
Тело – источник теплового излучения. В нем возникают стоячие электромагнитные волны, причем
Примеры применения уравнения Шредингера: частица в бесконечно глубокой потенциальной яме; гармонический осциллятор. Частица в бесконечно глубокой потенциальной яме:
0 ≤ х ≤ а: Граничные условия: Ψ(0)=0, Ψ(а)=0 Гармонические колебания
Энергия частицы квантуется.
Классическая частица в такой потенциальной яме может иметь любую энергию и, двигаясь равномерно от одной стенки к другой с равной вероятностью может быть поймана в любом месте ямы. У квантовой частицы энергия имеет линейчатый спектр и вероятность поймать ее в данной области ямы для разных состояний различна.
Гармонический осциллятор: (пружинный маятник)
Энергия такого осциллятора квантуется. Примером квантовых осцилляторов может служить колебание атомов в узлах кристаллической решетки. Согласно классическим представлениям Т~< ε > - средняя энергия теплового движения.
Квантовый осциллятор: Движение никогда не прекращается. Это проявляется в опыте.
Гармонический осциллятор, его закон движения, скорость, ускорение, возвращающая сила, энергия. Гармонический осциллятор – система, совершающая колебания, описываемые дифференциальным уравнением гармонических колебаний: За период колебаний фаза колебания получает приращение 2 π, т.е.: Запишем первую и вторую производные по времени от гармонически колеблющейся величины s:
Из последнего выражения и следует дифференциальное уравнение гармонических колебаний Пусть материальная точка совершает прямолинейные гармонические колебания вдоль оси координат х около положения равновесия, принятого за начало координат. Тогда зависимость координаты х от времени t задается уравнением, аналогичным уравнению (*), где s = x: Скорость и ускорение – это первая и вторая соответственно производные от х:
Сила F = ma, действующая на колеблющуюся м.т. массой m вышенаписанных уравнений, равна:
Кинетическая энерги я Потенциальная энергия Полная энергия Е: ВЫВОДЫ: 1. Колебания возникают при условии: а) положения равновесия Если уравнение движения имеет такой вид, то это гармонические колебания с Примерами гармонического осциллятора являются пружинный, физический и математический маятники, колебательный контур.
|
||||
|
Последнее изменение этой страницы: 2017-01-23; просмотров: 418; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.191.37.129 (0.011 с.) |

 . Решением этого уравнения является выражение:
. Решением этого уравнения является выражение:  (*), где A – максимальное значение колеблющейся величины (амплитуда колебания), ω0 – круговая (циклическая) частота, φ – начальная фаза колебания в момент времени t =0, (ω0t + φ) – фаза колебания в момент времени t. Фаза колебания определяет значение колеблющейся величины в момент времени t. Так как косинус изменяется в пределах от +1 до -1, то s может принимать значения от +А до –А.
(*), где A – максимальное значение колеблющейся величины (амплитуда колебания), ω0 – круговая (циклическая) частота, φ – начальная фаза колебания в момент времени t =0, (ω0t + φ) – фаза колебания в момент времени t. Фаза колебания определяет значение колеблющейся величины в момент времени t. Так как косинус изменяется в пределах от +1 до -1, то s может принимать значения от +А до –А.
 откуда:
откуда: 

 .
.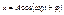

 где
где  .
. м.т., совершающей прямолинейные гармонические колебания равна:
м.т., совершающей прямолинейные гармонические колебания равна:  или
или 
 м.т., совершающей гармонические колебания под действием упругой силы F, равна
м.т., совершающей гармонические колебания под действием упругой силы F, равна  или
или 
 .
. 
 б) возвращающая сила
б) возвращающая сила  в) инертность, m. 2.
в) инертность, m. 2.  где ψ - колеблющаяся величина (x, v, A, F).
где ψ - колеблющаяся величина (x, v, A, F). .
.

 - зависит от сил трения.
- зависит от сил трения. Трение мало, δ мало. ωр≤ω0
Трение мало, δ мало. ωр≤ω0 Кольца Ньютона наблюдаются при интерференции света в тонком зазоре между соприкасающимися плоской и сферической поверхностями (рис.). В отраженном свете интерферируют лучи, разделяющиеся и вновь сходящиеся в точке А. Один из них отражается от границы раздела линза - воздух в этой точке, а другой проходит зазор и отражается от пластинки в точке А' с увеличением фазы на π.
Кольца Ньютона наблюдаются при интерференции света в тонком зазоре между соприкасающимися плоской и сферической поверхностями (рис.). В отраженном свете интерферируют лучи, разделяющиеся и вновь сходящиеся в точке А. Один из них отражается от границы раздела линза - воздух в этой точке, а другой проходит зазор и отражается от пластинки в точке А' с увеличением фазы на π. увеличивается вместе с увеличением толщины зазора при удалении от точки О, так что интерференционная картина имеет вид концентрических темных и светлых колец с центром в точке О. Интерференционная картина отчетлива при условии b «R.. Из рис. получаем:
увеличивается вместе с увеличением толщины зазора при удалении от точки О, так что интерференционная картина имеет вид концентрических темных и светлых колец с центром в точке О. Интерференционная картина отчетлива при условии b «R.. Из рис. получаем: 

 , где т - номер кольца (т = 0, 1,2...).
, где т - номер кольца (т = 0, 1,2...). Интерференционная картина в плоскопараллельных пластинках (пленках) определяется величинами l0, d, n и α. Для данных l0, d и n каждому наклону α лучей соответствует своя интерференционная полоса. Интерференционные полосы, возникающие в результате наложения лучей, падающих на плоскопараллельную пластинку под одинаковыми углами, называются полосами равного наклона.
Интерференционная картина в плоскопараллельных пластинках (пленках) определяется величинами l0, d, n и α. Для данных l0, d и n каждому наклону α лучей соответствует своя интерференционная полоса. Интерференционные полосы, возникающие в результате наложения лучей, падающих на плоскопараллельную пластинку под одинаковыми углами, называются полосами равного наклона. Просветление оптики. Для этого на свободные поверхности линз наносят тонкие пленки с показателем преломления меньшим, чем у материала линзы. При отражении света от границ раздела воздух — пленка и пленка — стекло возникает интерференция когерентных лучей 1' и 2' (рис.253). Толщину пленки d и показатели преломления стекла n с и пленки n можно подобрать так, чтобы интерферирующие лучи гасили друг друга. Для этого их амплитуды должны быть равны, а оптическая разность
Просветление оптики. Для этого на свободные поверхности линз наносят тонкие пленки с показателем преломления меньшим, чем у материала линзы. При отражении света от границ раздела воздух — пленка и пленка — стекло возникает интерференция когерентных лучей 1' и 2' (рис.253). Толщину пленки d и показатели преломления стекла n с и пленки n можно подобрать так, чтобы интерферирующие лучи гасили друг друга. Для этого их амплитуды должны быть равны, а оптическая разность
 - поперечная волна.
- поперечная волна.
 , каким-либо образом упорядочена.
, каким-либо образом упорядочена.
 Свет излучает атом. Каждый атом излучает линейно-поляризованный цуг волн (волновой цуг - излучение света атомами в виде отдельных коротких импульсов). Но т.к. атомы тела излучают хаотически, то естественный свет неполяризован.
Свет излучает атом. Каждый атом излучает линейно-поляризованный цуг волн (волновой цуг - излучение света атомами в виде отдельных коротких импульсов). Но т.к. атомы тела излучают хаотически, то естественный свет неполяризован. 




 , где I - интенсивность поляризованного света, прошедшего через поляризатор; I0 – интенсивность света, падающего на поляризатор; φ – угол, образованный вектором падающей световой волны с плоскостью поляризатора.
, где I - интенсивность поляризованного света, прошедшего через поляризатор; I0 – интенсивность света, падающего на поляризатор; φ – угол, образованный вектором падающей световой волны с плоскостью поляризатора.
 , отраженный луч полностью поляризован.
, отраженный луч полностью поляризован.

 где σ = 5,678 * 10-8 Вт/(м2 К2) – постоянная Стефана-Больцмана; Т - абсолютная температура.
где σ = 5,678 * 10-8 Вт/(м2 К2) – постоянная Стефана-Больцмана; Т - абсолютная температура. , где λ – длина волны, соответствующая максимальной испускательной способности абсолютно черного тела при данной температуре Т; b = 2,9 * 10-3 м К.
, где λ – длина волны, соответствующая максимальной испускательной способности абсолютно черного тела при данной температуре Т; b = 2,9 * 10-3 м К. , где h =6,625*10-34 Дж*с – постоянная Планка; ν – частота излучения.
, где h =6,625*10-34 Дж*с – постоянная Планка; ν – частота излучения. Пример резонатора – струна:
Пример резонатора – струна:

 , где m =1,2,3,…- номер гармоники.
, где m =1,2,3,…- номер гармоники.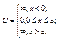




 - спектр собственных энергий частицы, уровни энергии.
- спектр собственных энергий частицы, уровни энергии. -собственные функции
-собственные функции ;
;  -собств. функции
-собств. функции
 .
.


 УШ→
УШ→ 
 , n - квантовое число (n = 0,1,2,…)
, n - квантовое число (n = 0,1,2,…)
 - энергия «нулевых» колебаний.
- энергия «нулевых» колебаний.


