
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Соотношения неопределенностей как выражение корпускулярно-волнового дуализма и границ применения классической физики.
Соотношения неопределенностей Гейзенберга являются математическим выражением корпускулярно-волнового дуализма, ограничивая применение классических моделей волны и частицы к микрочастицам. Классическая частица: состояние Ее координаты: x, y, z известны точно
Классическая волна:λ
Микрочастицы: Δх – неопределенность координаты Δрх - неопределенность импульса в проекции на эту ось.
Соотношения неопределенностей позволяют провести четкую границу между необходимостью использования квантовой или классической физики. Δх Δ Δх Δрх >> h – классический объект; Δх Δрх < h – таких объектов нет! Сопряженные величины: ΔЕ Δt ≥ h, где ΔЕ – неопределенность энергии; Δt – время, необходимое для измерения этого значения энергии Е. Экспериментальным подтверждением служит естественная ширина спектральных линий.
Состояние и уравнение движения квантовой частицы. Волновая функция, ее статистический смысл. Уравнение Шредингера. Классическая частица: м.т., состояние Уравнение движения: II закон Ньютона
Уравнение движения: УШ + граничные условия→Ψ Состояние квантового объекта полностью описывается волновой функцией Физический смысл имеет квадрат модуля волновой функции Вероятность ~ Плотность вероятности: Волновая функция конечная, однородная и непрерывная. Уравнение движения (Уравнение Шредингера):
Если известна U=U(x) и граничные условия (аналог начальных условий)
Примеры применения уравнения Шредингера: частица в бесконечно глубокой потенциальной яме; гармонический осциллятор. Частица в бесконечно глубокой потенциальной яме:
0 ≤ х ≤ а: Граничные условия: Ψ(0)=0, Ψ(а)=0 Гармонические колебания
Энергия частицы квантуется.
Классическая частица в такой потенциальной яме может иметь любую энергию и, двигаясь равномерно от одной стенки к другой с равной вероятностью может быть поймана в любом месте ямы. У квантовой частицы энергия имеет линейчатый спектр и вероятность поймать ее в данной области ямы для разных состояний различна.
Гармонический осциллятор: (пружинный маятник)
Энергия такого осциллятора квантуется. Примером квантовых осцилляторов может служить колебание атомов в узлах кристаллической решетки. Согласно классическим представлениям Т~< ε > - средняя энергия теплового движения.
Квантовый осциллятор: Движение никогда не прекращается. Это проявляется в опыте.
|
|||||
|
Последнее изменение этой страницы: 2017-01-23; просмотров: 270; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.117.196.217 (0.01 с.) |
 - траектория
- траектория
 неопределенность (ошибка) координаты.
неопределенность (ошибка) координаты.
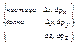 сопряженные величины.
сопряженные величины.


 Для Δх и Δрх (и т.п.) ограничений нет.
Для Δх и Δрх (и т.п.) ограничений нет. рх ≥ h – квантовый объект;
рх ≥ h – квантовый объект; - траектория.
- траектория. .
. Микрочастица: волна + частица; Δx + Δpx ≥ h – нет классической траектории, волновое «облако».
Микрочастица: волна + частица; Δx + Δpx ≥ h – нет классической траектории, волновое «облако». . Сама волновая функция не сопоставима ни с какой измеряемой в опыте физической величиной.
. Сама волновая функция не сопоставима ни с какой измеряемой в опыте физической величиной.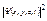 , определяющий вероятность обнаружения микрочастицы в точке с координатами x,y,z в момент времени t. Это значит, что
, определяющий вероятность обнаружения микрочастицы в точке с координатами x,y,z в момент времени t. Это значит, что  прямо пропорциональна потоку частиц N, который может быть измерен, например, счетчиком: N ~
прямо пропорциональна потоку частиц N, который может быть измерен, например, счетчиком: N ~  ~
~ 
 ~ ΔN.
~ ΔN.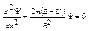 - Одномерное стационарное движение.
- Одномерное стационарное движение.
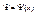 , U- потенциальная энергия частицы (энергия взаимодействия); Е - полная энергия; m – масса частицы.
, U- потенциальная энергия частицы (энергия взаимодействия); Е - полная энергия; m – масса частицы. - на границах области движения.
- на границах области движения.
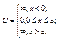




 - спектр собственных энергий частицы, уровни энергии.
- спектр собственных энергий частицы, уровни энергии. -собственные функции
-собственные функции ;
;  -собств. функции
-собств. функции
 .
.


 УШ→
УШ→ 
 , n - квантовое число (n = 0,1,2,…)
, n - квантовое число (n = 0,1,2,…)
 - энергия «нулевых» колебаний.
- энергия «нулевых» колебаний.


