
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Волна, уравнение гармонической волны.Содержание книги
Поиск на нашем сайте
Процесс распространения колебаний в сплошной среде (в пространстве и времени) называется волновым процессом (или волной). При распространении волны частицы среды не движутся вместе с волной, а колеблются около своих положений равновесия. Вместе с волной от частицы к частице среды передаются лишь состояние колебательного движения и его энергия. Поэтому основным свойством всех волн, независимо от их природы, является перенос энергии без переноса вещества. Среди разнообразных типов волн, встречающихся в природе и технике, выделяются следующие их типы: волны на поверхности жидкости, упругие и электромагнитные волны. Упругими (механическими) волнами называются механические возмущения, распространяющиеся в упругой среде. Упругие волны бывают продольные и поперечные. Упругая волна называется гармонической, если соответствующие ей колебания частиц среды являются гармоническими. Гармоническая поперечная волна, распространяющаяся со скоростью v вдоль оси x представлена на рис., т.е. приведена зависимость между смещением ξ частиц среды, участвующих в волновом процессе, и расстоянием x этих частиц (напр., частицы В) от источника колебаний О для какого-то фиксированного момента времени t. Длина волны: Область пространства, где уже возникли колебания, называется волновым полем. Поверхность, отделяющая волновое поле от невозмущенной среды называется фронтом волны. Точки волнового поля, колеблющиеся одинаково образуют волновые поверхности. Форма волновых поверхностей и фронта волны бывает различной и определяет название волны: плоская, сферическая, цилиндрическая и т.д. Для вывода уравнения бегущей волны рассмотрим плоскую волну, предполагая, что колебания носят гармонический характер, а ось x совпадает с направлением распространения волны. Рассмотрим некоторую частицу В среды. Колебания этой частицы отстают от колебаний источника на τ. τ=х/υ, где υ - скорость частицы. Тогда уравнение колебаний частиц, лежащих в плоскости х, имеет вид: В общем случае уравнение плоской волны имеет вид: Для характеристики волн используется волновое число: Учитывая это число уравнению можно придать вид:
|
|||||||||||||||||||
|
Последнее изменение этой страницы: 2017-01-23; просмотров: 274; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.144.158.98 (0.008 с.) |

 - расстояние между ближайшими частицами, колеблющимися в одинаковой фазе.
- расстояние между ближайшими частицами, колеблющимися в одинаковой фазе.  , где ν – частота колебаний,
, где ν – частота колебаний,  .
. откуда следует, что ξ(x, t) является не только периодической функцией времени, но и периодической функцией координаты х. Если плоская волна распространяется в положительном направлении, то
откуда следует, что ξ(x, t) является не только периодической функцией времени, но и периодической функцией координаты х. Если плоская волна распространяется в положительном направлении, то 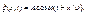
 где А=const – амплитуда волны, ω – циклическая частота, φ0 – начальная фаза волны.
где А=const – амплитуда волны, ω – циклическая частота, φ0 – начальная фаза волны.




