
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Электромагнитное поле. Уравнения Максвелла. Плоская электромагнитная волна.Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Уравнения Максвелла для электромагнитного поля В основе теории Максвелла лежат рассмотренные выше четыре уравнения: 1. Электрическое поле может быть как потенциальным (e q), так и вихревым (Е B), поэтому напряженность суммарного поля Е = Е Q+ Е B. Так как циркуляция вектора e q равна нулю, а циркуляция вектора Е B определяется выражением: 2. Обобщенная теорема о циркуляции вектора Н: Это уравнение показывает, что магнитные поля могут возбуждаться либо движущимися зарядами (электрическими токами), либо переменными электрическими полями. 3. Теорема Гаусса для поля D: Если заряд распределен внутри замкнутой поверхности непрерывно с объемной плотностью r, то формула запишется в виде: 4. Теорема Гаусса для поля В: Итак, полная система уравнений Максвелла в интегральной форме:
Величины, входящие в уравнения Максвелла, не являются независимыми и между ними существует следующая связь (изотропные не сегнетоэлектрические и не ферромагнитные среды): D =e0e E, В= m0m Н, j =g E, где e0 и m0 — соответственно электрическая и магнитная постоянные, e и m— соответственно диэлектрическая и магнитная проницаемости, g — удельная проводимость вещества. Из уравнений Максвелла вытекает, что источниками электрического поля могут быть либо электрические заряды, либо изменяющиеся во времени магнитные поля, а магнитные поля могут возбуждаться либо движущимися электрическими зарядами (электрическими токами), либо переменными электрическими полями. Уравнения Максвелла не симметричны относительно электрического и магнитного полей. Это связано с тем, что в природе существуют электрические заряды, но нет зарядов магнитных.
10. Интерференция. Когерентность волн. Условия максимума и минимума интерференции. <?>Принцип получения когерентных световых волн<?>. Интерференция волн
Рассмотрим наложение двух когерентных сферических волн, возбуждаемых точечными источниками S1 и S2 (рис.221), колеблющимися с одинаковыми амплитудой ао и частотой СО и постоянной разностью фаз. Согласно уравнению сферической волны
где r 1 и r 2 — расстояния от источников волн до рассматриваемой точки В, k — волновое число, (j1 и j2 — начальные фазы обеих накладывающихся сферических волн. Амплитуда результирующей волны в точке В равна: Так как для когерентных источников разность начальных фаз (j1-j2)=const, то результат наложения двух волн в различных точках зависит от величины D= r 1- r 2, называемой разностью хода волн. В точках, где k (r 1 -r 2 )- (j1-j2)=±2mp (m=0, 1,2,...), наблюдается интерференционный максимум: амплитуда результирующего колебания A=A 0 /r 1 +A0/r 2. В точках, где k (r 1- r 2) - (j1-j2)= ±(2m+1)p (m=0, 1,2,...), наблюдается интерференционный минимум: амплитуда результирующего колебания А=А 0 /r 1 —А 0 /r 2│(m=0, 1, 2,...,) называется соответственно порядком интерференционного максимума или минимума. Эти Условия сводятся к тому, что r 1 -r 2=const. Интерференция света Возникает при сложении двух (или более) световых волн, когда в одних местах волны гасят друг друга, а в других – усиливают, т.е. происходит перераспределение энергии вдоль фронта волны с образованием максимумов и минимумов интенсивности. Для световых волн максимумы ярко освещены, минимумы – слабо (темные области). Интерференционная картина устойчива во времени.
11. Интерференция света в тонких пленках, примеры ее наблюдения и применения. При падении на тонкую прозрачную пластинку (пленку) (рис.) луч в точке А делится на два: отраженный – 1 и преломленный – 2, который после отражения от нижней плоскости пленки в точке О и преломления в точке С идет параллельно лучу 1. Попадая на линзу (хрусталик глаза), эти лучи собираются водной точке и интерферируют.
Здесь учитывается, что при отражении волны 1 в точке А от оптически более плотной среды происходит увеличение ее фазы на π, что равносильно дополнительному пути В проходящем свете интерферируют лучи, отраженные от оптически менее плотной среды, так что разность хода уменьшается на Кольца Ньютона
Разность хода этих лучей: Радиусы светлых колец в отраженном свете (или темных в проходящем): радиусы темных колец в отраженном свете (или светлых в проходящем): Полосы равного наклона (интерференция от плоскопараллельной пластинки)
Лучи 1' и 1 ", отразившиеся от верхней и нижней граней пластинки (рис.250), параллельны друг другу, так как пластинка плоскопараллельна. Следовательно, интерферирующие лучи 1 ' и 1 " «пересекаются» только в бесконечности, поэтому говорят, что полосы равного наклона локализованы в бесконечности. Для их наблюдения используют собирающую линзу и экран (Э), расположенный в фокальной плоскости линзы. Параллельные лучи 1' и 1" соберутся в фокусе F линзы (на рис. 250 ее оптическая ось параллельна лучам 1' и 1"), в эту же точку придут и другие лучи (на рис.250 — луч 2), параллельные лучу 1, в результате чего увеличивается общая интенсивность. Лучи 3, наклоненные под другим углом, соберутся в другой точке Р фокальной плоскости линзы. Легко показать, что если оптическая ось линзы перпендикулярна поверхности пластинки, то полосы равного наклона будут иметь вид концентрических колец с центром в фокусе линзы. Применение интерференции света Явление интерференции обусловлено волновой природой света; его количественные закономерности зависят от длины волны l0.Поэтому это явление применяется для подтверждения волновой природы света и для измерения длин волн (интерференционная спектроскопия). Явление интерференции применяется также для улучшения качества оптических приборов (просветление оптики) и получения высокоотражающих покрытий.
хода — равна (2m+1)l0/2. Явление интерференции также применяется в очень точных измерительных приборах, называемых интерферометрами. Все интерферометры основаны на одном и том же принципе и различаются лишь конструкционно. Интерферометры — очень чувствительные оптические приборы, позволяющие определять незначительные изменения показателя преломления прозрачных тел (газов, жидких и твердых тел) в зависимости от давления, температуры, примесей и т. д.
|
||
|
Последнее изменение этой страницы: 2017-01-23; просмотров: 639; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.214 (0.008 с.) |

 Электромагнитная волна – это распространяющееся в пространстве электромагнитное поле. Оно может существовать в вакууме, поэтому электромагнитные волны могут распространяться в вакууме. Плоская электромагнитная волна представлена на рисунке.
Электромагнитная волна – это распространяющееся в пространстве электромагнитное поле. Оно может существовать в вакууме, поэтому электромагнитные волны могут распространяться в вакууме. Плоская электромагнитная волна представлена на рисунке.
 , то циркуляция вектора напряженности суммарного поля:
, то циркуляция вектора напряженности суммарного поля:  Это уравнение показывает, что источниками электрического поля могут быть не только электрические заряды, но и меняющиеся во времени магнитные поля.
Это уравнение показывает, что источниками электрического поля могут быть не только электрические заряды, но и меняющиеся во времени магнитные поля.





 Согласованное протекание во времени и пространстве нескольких колебательных или волновых процессов связывают с понятием когерентности. Волныназываются когерентными, если разность их фаз остается постоянной во времени. Очевидно, что когерентными могут быть лишь волны, имеющие одинаковую частоту. При наложении в пространстве двух (или нескольких) когерентных волн в разных его точках получается усиление или ослабление результирующей волны в зависимости от соотношения между фазами этих волн. Это явление называется интерференцией волн.
Согласованное протекание во времени и пространстве нескольких колебательных или волновых процессов связывают с понятием когерентности. Волныназываются когерентными, если разность их фаз остается постоянной во времени. Очевидно, что когерентными могут быть лишь волны, имеющие одинаковую частоту. При наложении в пространстве двух (или нескольких) когерентных волн в разных его точках получается усиление или ослабление результирующей волны в зависимости от соотношения между фазами этих волн. Это явление называется интерференцией волн. :
:
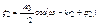 ,
,
 - условие максимума, (m=0, 1, 2,…);
- условие максимума, (m=0, 1, 2,…); - условие минимума.
- условие минимума. Оптическая разность хода лучей равна:
Оптическая разность хода лучей равна: 
 . Расчет дает, что:
. Расчет дает, что: 
 Кольца Ньютона наблюдаются при интерференции света в тонком зазоре между соприкасающимися плоской и сферической поверхностями (рис.). В отраженном свете интерферируют лучи, разделяющиеся и вновь сходящиеся в точке А. Один из них отражается от границы раздела линза - воздух в этой точке, а другой проходит зазор и отражается от пластинки в точке А' с увеличением фазы на π.
Кольца Ньютона наблюдаются при интерференции света в тонком зазоре между соприкасающимися плоской и сферической поверхностями (рис.). В отраженном свете интерферируют лучи, разделяющиеся и вновь сходящиеся в точке А. Один из них отражается от границы раздела линза - воздух в этой точке, а другой проходит зазор и отражается от пластинки в точке А' с увеличением фазы на π. увеличивается вместе с увеличением толщины зазора при удалении от точки О, так что интерференционная картина имеет вид концентрических темных и светлых колец с центром в точке О. Интерференционная картина отчетлива при условии b «R.. Из рис. получаем:
увеличивается вместе с увеличением толщины зазора при удалении от точки О, так что интерференционная картина имеет вид концентрических темных и светлых колец с центром в точке О. Интерференционная картина отчетлива при условии b «R.. Из рис. получаем: 

 , где т - номер кольца (т = 0, 1,2...).
, где т - номер кольца (т = 0, 1,2...). Интерференционная картина в плоскопараллельных пластинках (пленках) определяется величинами l0, d, n и α. Для данных l0, d и n каждому наклону α лучей соответствует своя интерференционная полоса. Интерференционные полосы, возникающие в результате наложения лучей, падающих на плоскопараллельную пластинку под одинаковыми углами, называются полосами равного наклона.
Интерференционная картина в плоскопараллельных пластинках (пленках) определяется величинами l0, d, n и α. Для данных l0, d и n каждому наклону α лучей соответствует своя интерференционная полоса. Интерференционные полосы, возникающие в результате наложения лучей, падающих на плоскопараллельную пластинку под одинаковыми углами, называются полосами равного наклона. Просветление оптики. Для этого на свободные поверхности линз наносят тонкие пленки с показателем преломления меньшим, чем у материала линзы. При отражении света от границ раздела воздух — пленка и пленка — стекло возникает интерференция когерентных лучей 1' и 2' (рис.253). Толщину пленки d и показатели преломления стекла n с и пленки n можно подобрать так, чтобы интерферирующие лучи гасили друг друга. Для этого их амплитуды должны быть равны, а оптическая разность
Просветление оптики. Для этого на свободные поверхности линз наносят тонкие пленки с показателем преломления меньшим, чем у материала линзы. При отражении света от границ раздела воздух — пленка и пленка — стекло возникает интерференция когерентных лучей 1' и 2' (рис.253). Толщину пленки d и показатели преломления стекла n с и пленки n можно подобрать так, чтобы интерферирующие лучи гасили друг друга. Для этого их амплитуды должны быть равны, а оптическая разность



