
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Разрешающая способность дифракционной решеткиСодержание книги Похожие статьи вашей тематики
Поиск на нашем сайте
где Dl — наименьшая разность длин волн двух соседних спектральных линий (l и l+Dl,), при которой эти линии могут быть видны раздельно в спектре, полученном посредством данной решетки; N — полное число щелей решетки. Угловая дисперсия дифракционной решетки
Линейная дисперсия дифракционной решетки
где F — фокусное расстояние линзы, проектирующей спектр на экран. Формула Вульфа — Брэгга
где q — угол скольжения (угол между направлением параллельного пучка рентгеновского излучения, падающего на кристалл, и атомной плоскостью в кристалле); d — расстояние между атомными плоскостями кристалла. Разрешающая способность (разрешающая сила) объектива
где dy — наименьшее угловое расстояние между двумя точками, при котором они еще разрешаются оптическим прибором, D - диаметр объектива, l - длина волны света. Закон Брюстера
где eB — угол падения, при котором отразившийся от диэлектрика луч полностью поляризован; n 21 — относительный показатель преломления второй среды относительно первой. Закон Малюса
где I о — интенсивность плоскополяризованного света, падающего на анализатор; I — интенсивность этого света после анализатора; a — угол между направлением колебаний электрического вектора света, падающего на анализатор, и плоскостью пропускания анализатора (если колебания электрического вектора падающего света совпадают с этой плоскостью, то анализатор пропускает данный свет без ослабления). Угол поворота плоскости поляризации монохроматического света при прохождении через оптически активное вещество: а) где a — постоянная вращения; d — длина пути, пройденного светом в оптически активном веществе; б) где [a] — удельное вращение; r—массовая концентрация оптически активного вещества в растворе. Релятивистская масса
где m o — масса покоя частицы; v — ее скорость; с —-скорость света в вакууме; b— скорость частицы, выраженная в долях скорости света (b= v/с). Взаимосвязь массы и энергии релятивистской частицы
где Полная энергия свободной частицы
где Т — кинетическая энергия релятивистской частицы. Кинетическая энергия релятивистской частицы
Импульс релятивистской частицы
Связь между полной энергией и импульсом релятивистской частицы
Закон Стефана—Больцмана
где Re — энергетическая светимость абсолютно черного тела, s — постоянная Стефана— Больцмана; Т — термодинамическая температура Кельвина. Если тело не является абсолютно черным, то закон Стефана—Больцмана применяют в виде
где a— коэффициент (степень) черноты тела (a <1). Закон смещения Вина
где l m — длина волны, на которую приходится максимум энергии излучения; b — постоянная Вина. Максимальная спектральная плотность энергетической светимости абсолютно черного тела
где С 1 = 1,29 10-5 Вт/(м3 К5). Энергия фотона
где h — постоянная Планка; Масса фотона
где с — скорость света в вакууме; l — длина волны фотона. Импульс фотона
Формула Эйнштейна для фотоэффекта
где h n — энергия фотона, падающего на поверхность металла; А — работа выхода электрона; T max — максимальная кинетическая энергия фотоэлектрона. Красная граница фотоэффекта
где no — минимальная частота света, при которой еще возможен фотоэффект; lо — максимальная длина волны света, при которой еще возможен фотоэффект; h — постоянная Планка; с — скорость света в вакууме. Формула Комптона
где l1 — длина волны фотона, встретившегося со свободным или слабосвязанным электроном; l2 — длина волны фотона, рассеянного на угол q после столкновения с электроном; т о — масса покоящегося электрона. Комптоновская длина волны
Давление света при нормальном падении на поверхность
где Ее — энергетическая освещенность, w — объемная плотность энергии излучения; r — коэффициент отражения. Момент импульса электрона согласно теории Бора для атома водорода
где m — масса электрона; vn — скорость электрона на n -й орбите; rn — радиус n -й стационарной орбиты; ћ = h /2p — постоянная Планка; п — главное квантовое число (n = 1, 2,3,...). Радиус n -й стационарной орбиты
где a o — первый боровский радиус. Энергия электрона в атоме водорода
где Ei — энергия ионизации атома водорода. Энергия, излучаемая или поглощаемая атомом водорода,
где п 1 и п 2 — квантовые числа, соответствующие энергетическим уровням, между которыми совершается переход электрона в атоме. Спектроскопическое волновое число
где l — длина волны излучения или поглощения атомом; R — постоянная Ридберга. Длина волны де Бройля
где р — импульс частицы. Импульс частицы и его связь с кинетической энергией Т: a) б) где т о — масса покоя частицы; т — релятивистская масса; v — скорость частицы; с — скорость света в вакууме; Е o — энергия покоя частицы (Е o = т о c 2) Соотношение неопределенностей: а) где D рx, — неопределенность проекции импульса на ось X,D х — неопределенность координаты; б) где D E — неопределенность энергии; D t — время жизни квантовой системы в данном энергетическом состоянии. Одномерное уравнение Шредингера для стационарных состояний
где y= y(х) — волновая функция, описывающая состояние частицы; т — масса частицы; Е — полная энергия; U = U(x) — потенциальная энергия частицы. Плотность вероятности
где dw(x) — вероятность того, что частица может быть обнаружена вблизи точки с координатой х на участке dx. Вероятность обнаружения частицы в интервале от х 1 до х 2
Решение уравнения Шредингера для одномерного, бесконечно глубокого, прямоугольного потенциального ящика: а) б) где п— квантовое число (п = 1, 2, 3,...); l— ширина ящика. В области 0 < x < l U =¥ и y(х)=0. Массовое число ядра (число нуклонов в ядре)
где Z — зарядовое число (число протонов); N — число нейтронов. Закон радиоактивного распада
где dN — число ядер, распадающихся за интервал времени dt, N — число ядер, не распавшихся к моменту времени t; N o — число ядер в начальный момент (t o=0); l — постоянная радиоактивного распада. Число ядер, распавшихся за время t,
В случае, если интервал времени D t, за который определяется число распавшихся ядер, много меньше периода полураспада T 1/2, то число распавшихся ядер можно определить по формуле
Зависимость периода полураспада от постоянной радиоактивного распада
Среднее время t жизни радиоактивного ядра, т. е. интервал времени, за который число нераспавшихся ядер уменьшается в е раз,
Число атомов N, содержащихся радиоактивном изотопе,
где m— масса изотопа; m — молярная масса; Na— постоянная Авогадро. Активность А радиоактивного изотопа
где dN — число ядер, распадающихся за интервал времени dt; A o — активность изотопа в начальный момент времени. Удельная активность изотопа
Дефект массы ядра,
где Z — зарядовое число (число протонов в ядре); А — массовое число (число нуклонов в ядре); (А—Z) — число нейтронов в ядре; mp — масса протона; mn — масса нейтрона; mядр — масса ядра. Изменение энергии при ядерной реакции определяется соотношением
где å M 1—сумма масс частиц до реакции и å M 2—сумма масс частиц после реакции. Если å M 1 > å M 2, то реакция идет с выделением энергии, если же å M 1 < å M 2, то реакция идет с поглощением энергии. Отметим, что в последнюю формулу так же, как и при вычислении энергии связи ядра, мы можем подставлять массу изотопов, а не ядер, так как поправки на массу электронов оболочки входят с разными знаками и поэтому исключаются. Энергия связи ядра
где D m — дефект массы ядра; с — скорость света в вакууме. Во внесистемных единицах энергия связи ядра равна E св= 931 D m, где дефект массы D m —в а.е.м.; 931— коэффициент пропорциональности (1 а.е.м.~931 МэВ). Контрольные задачи 1. На пути пучка света поставлена стеклянная пластина толщиной d =1 мм так, что угол падения луча i 1=30°. На сколько изменится оптическая длина пути светового пучка? 2. На мыльную пленку с показателем преломления п =1,33 падает по нормали монохроматический свет с длиной волны l=0,6 мкм. Отраженный свет в результате интерференции имеет наибольшую яркость. Какова наименьшая возможная толщина d min пленки? 3. Между стеклянной пластинкой и лежащей на ней плосковыпуклой линзой находится жидкость. Найти показатель преломления жидкости, если радиус r 3 третьего темного кольца Ньютона при наблюдении в отраженном те с длиной волны l=0,6 мкм равен 0,82 мм. Радиус кривизны линзы R =0,5 м. 4. Радиус второго темного кольца Ньютона в отраженном свете r 2=0,4 мм. Определить радиус R кривизны плосковыпуклой линзы, взятой для опыта, если она освещается монохроматическим светом с длиной волны l=0,64 мкм. 5. На тонкую пленку в направлении нормали к ее поверхности падает монохроматический свет с длиной волны l=500 нм. Отраженный от нее свет максимально усилен вследствие интерференции. Определить минимальную толщину d min пленки, если показатель преломления материала пленки п =1,4. 6. Расстояние L от щелей до экрана в опыте Юнга равно 1 м. Определить расстояние между щелями, если на отрезке длиной l =1 см укладывается N =10 темных интерференционных полос. Длина волны l=0,7 мкм. 7. На стеклянную пластину положена выпуклой стороной плосковыпуклая линза. Сверху линза освещена монохроматическим светом длиной волны l=500 нм, найти радиус R линзы, если радиус четвертого, темного кольца Ньютона в отраженном свете r 4=2 мм. 8. На тонкую глицериновую пленку толщиной d =1,5 мкм нормально к ее поверхности падает белый свет. Определить длины волн лучей видимого участка спектра (0,4<l<0,8 мкм), которые будут ослаблены в результате интерференции. 9. На стеклянную пластину нанесен тонкий слой прозрачного вещества с показателем преломления п =1,3. Пластинка освещена параллельным пучком монохроматического света с длиной волны l=640 нм, падающим на пластинку нормально. Какую минимальную толщину d min должен иметь слой, чтобы отраженный пучок имел наименьшую яркость? 10. На тонкий стеклянный клин падает нормально параллельный пучок света с длиной волны l=500 нм. Расстояние между соседними темными интерференционными полосами в отраженном свете b =0,5 мм. Определить угол a между поверхностями клина. Показатель преломления стекла, из которого изготовлен клин, п =1,6. 11. Плосковыпуклая стеклянная линза с фокусным расстоянием F =1 м лежит выпуклой стороной на стеклянной пластинке. Радиус пятого темного кольца Ньютона в отраженном свете r 5=1,1 мм. Определить длину световой волны l. 12. Между двумя плоскопараллельными пластинами на расстоянии L =10 см от границы их соприкосновения находится проволока диаметром d =0,01 мм, образуя воздушный клин. Пластины освещаются нормально падающим монохроматическим светом (l=0,6 мкм). Определить ширину b интерференционных полос, наблюдаемых в отраженном свете. 13. Установка для наблюдения колец Ньютона освещается нормально падающим монохроматическим светом (l=590 нм). Радиус кривизны R линзы равен 5 см. Определить толщину d 3 воздушного промежутка в том месте, где в отраженном свете наблюдается третье светлое кольцо. 14. Точечный источник света с l=500 нм помещен на расстоянии а =0,500 м перед непрозрачной преградой с отверстием радиуса r =0,500 мм. Определить расстояние b от преграды до точки, для которой число m открываемых отверстием зон Френеля будет равно: а) 1, б) 5, в) 10. 15. Точечный источник света с l=550 нм помещен на расстоянии а =1,00 м перед непрозрачной преградой с отверстием радиуса r =2,00 мм. а) Какое минимальное число m min открытых зон Френеля может наблюдаться при этих условиях? б) При каком значении расстояния b от преграды до точки наблюдения получается минимально возможное число открытых зон? в) При каком радиусе r отверстия может оказаться в условиях данной задачи открытой только одна центральная зона Френеля? 16. Исходя из определения зон Френеля, найти число m зон Френеля, которые открывает отверстие радиуса r для точки, находящейся на расстоянии b от центра отверстия, в случае если волна, падающая на отверстие, плоская. 17. На непрозрачную преграду с отверстием радиуса r =1,000 мм падает плоская монохроматическая световая волна. Когда расстояние от преграды до установленного за ней экрана равно b 1=0,575 м, в центре дифракционной картины наблюдается максимум интенсивности. При увеличении расстояния до значения b 2=0,862 м максимум интенсивности сменяется минимумом. Определить длину волны λ света. 18. Интенсивность, создаваемая на экране некоторой монохроматической световой волной в отсутствие преград, равна I o. Какова будет интенсивность I в центре дифракционной картины, если на пути волны поставить преграду с круглым отверстием, открывающим: а) 1-ю зону Френеля, б) половину 1-й зоны Френеля, в) полторы зоны Френеля, г) треть 1-й зоны Френеля? 19. Свет от монохроматического источника (λ=0,6 мкм) падает нормально на диафрагму с круглым отверстием. Диаметр отверстия 6 мм. За диафрагмой на расстоянии 3 м от нее находится экран. 1) Сколько зон Френеля укладывается в отверстии диафрагмы? 2) Каким будет центр дифракционной картины на экране: темным или светлым? 20. Вычислить радиусы первых пяти зон Френеля, если расстояние от источника света до волновой поверхности равно 1 м, расстояние от волновой поверхности до точки наблюдения также равно 1 м и λ=5·10-7 м. 21. Вычислить радиусы первых пяти зон Френеля для случая плоской волны. Расстояние от волновой поверхности до точки наблюдения равно 1 м. Длина волны λ=5·10-7 м. 22. Дифракционная картина наблюдается на расстоянии l от точечного источника монохроматического света (λ=6·10-5 см). На расстоянии 0,5 l от источника помещена круглая непрозрачная преграда диаметром 1 см. Чему равно расстояние l, если преграда закрывает только центральную зону Френеля? 23. На пластину с щелью, ширина которой а =0,05 мм, падает нормально монохроматический свет с длиной волны l=0,7 мкм. Определить угол j отклонения лучей, соответствующий первому дифракционному максимуму. 24. Какое наименьшее число N min штрихов должна содержать дифракционная решетка, чтобы в спектре второго порядка можно было видеть раздельно две желтые линии натрия с длинами волн l1=589,0 нм и l2=589,6 нм? Какова длина l такой решетки, если постоянная решетки d =5 мкм? 25. Дифракционная решетка, освещенная нормально падающим монохроматическим светом, отклоняет спектр третьего порядка на угол j1=30°. На какой угол j2 отклоняет она спектр четвертого порядка? 26. На поверхность дифракционной решетки нормально к ее поверхности падает монохроматический свет. Постоянная дифракционной решетки в п =4,6 раза больше длины световой волны. Найти общее число m max дифракционных максимумов, которые теоретически можно наблюдать в данном случае. 27. На дифракционную решетку падает нормально параллельный пучок белого света. Спектры третьего и четвертого порядка частично накладываются друг на друга. На какую длину волны в спектре четвертого порядка накладывается граница (l=780 нм) спектра третьего порядка? 28. На дифракционную решетку, содержащую п =600 штрихов на миллиметр, падает нормально белый свет. Спектр проецируется помещенной вблизи решетки линзой на экран. Определить длину l спектра первого порядка на экране, если расстояние от линзы до экрана 11,2 м. Границы видимого спектра: lкр=780 нм, lф=400 нм. 29. На грань кристалла каменной соли падает параллельный пучок рентгеновского излучения. Расстояние между атомными плоскостями равно 280 пм. Под углом в q=65° к атомной плоскости наблюдается дифракционный максимум первого порядка. Определить длину волны l рентгеновского излучения. 30. На непрозрачную пластину с узкой щелью падает нормально плоская монохроматическая световая волна (l=600 нм). Угол отклонения лучей, соответствует второму дифракционному максимуму, j=20°. Определить ширину а щели. 31. На дифракционную решетку, содержащую п =100 штрихов на 1 мм, нормально падает монохроматический свет. Зрительная труба спектрометра наведена на максимум второго порядка. Чтобы навести трубу на другой максимум того же порядка, ее нужно повернуть на угол Dj=16°. Определить длину волны l света, падающего на решетку. 32. На дифракционную решетку падает нормально монохроматический свет (l=410 нм). Угол Dj между направлениями на максимумы первого и второго порядка равен 2°21". Определить число п штрихов на 1 мм дифракционной решетки. 33. Постоянная дифракционной решетки в п =4 раза больше длины световой волны монохроматического света, нормально падающего на ее поверхность. Определить угол a. между двумя первыми симметричными дифракционными максимумами. 34. Расстояние между штрихами дифракционной решетки d =4 мкм. На решетку падает нормально свет длиной волны l=0,58 мкм. Максимум какого наибольшего порядка дает эта решетка? 35. Определить угловую дисперсию дифракционной решетки для λ=589 нм в спектре первого порядка. Постоянная решетки равна 2,5·10-4 см. 36. Угловая дисперсия дифракционной решетки для λ=668 нм в спектре первого порядка равна 2,02·105 рад/м. Найти период дифракционной решетки. 37. Найти линейную дисперсию (в мм/нм) дифракционной решетки предыдущей задачи, если фокусное расстояние линзы, проектирующей спектр на экран, равно 40 см. 38. На каком расстоянии друг от друга будут находиться на экране две линии ртутной дуги (λ1=577 нм и λ2=579,1 нм) в спектре первого порядка, полученном при помощи дифракционной решетки с периодом 2·10-4 см? Фокусное расстояние линзы, проектирующей спектр на экран, равно 0,6 м. 39. На дифракционную решетку нормально падает пучок света. Красная линия (λ.=630 нм) видна в спектре третьего порядка под углом φ=60°. Какая спектральная линия видна под этим же углом в спектре четвертого порядка? 2) Какое число штрихов на 1 мм, длины имеет дифракционная решетка? 3) Чему равна угловая дисперсия этой решетки для линии λ=630 нм в спектре третьего порядка? 40. Для какой длины волны дифракционная решетка с постоянной d =5 мкм имеет угловую дисперсию D = 6,3·105 рад/м в спектре третьего порядка? 41. Почему в случае отражательной решетки удается наблюдать дифракционные максимумы малых порядков при периодах решетки d, много больших длины волны λ, например, при d ~ l мм? 42. Можно ли различить невооруженным глазом два находящихся на расстоянии 5 км столба, отстоящих друг от друга на 1 м? Диаметр зрачка принять равным 4 мм. 43. В зрительную трубу рассматривается лунная поверхность. Диаметр объектива трубы d =4,00 см. При каком минимальном расстоянии a min между двумя кратерами их можно увидеть раздельно? Длину световой волны принять равной 600 нм. 44. Пластинку кварца толщиной d =2 мм поместили между параллельными призмами Николя, в результате чего плоскость поляризации монохроматического света повернулась на угол j=53°. Какой наименьшей толщины следует взять пластинку, чтобы поле зрения поляризатора стало совершенно темным? 45. Параллельный пучок света переходит из глицерина в стекло так, что пучок, отраженный от границы раздела этих сред, оказывается максимально поляризованным. Определить угол j между падающим и преломленным пучками. 46. Кварцевую пластинку поместили между скрещенными призмами Николя. При какой наименьшей толщине d minкварцевой пластины поле зрения между призмами Николя будет максимально просветлено? Постоянная вращения a кварца равна 27 град/мм. 47. При прохождении света через трубку длиной l 1=20 см, содержащую раствор сахара концентрацией C 1=10%, плоскость поляризации света повернулась на угол j1=13,3°. В другом растворе сахара, налитом в трубку длиной l 2=15 см, плоскость поляризации повернулась на угол j2=5,2°. Определить концентрацию C 2 второго раствора. 48. Пучок света последовательно проходит через две призмы Николя, плоскости пропускания которых образуют между собой угол j=40°. Принимая, что коэффициент поглощения k каждой призмы равен 0,15, найти, во сколько раз пучок света, выходящий из второй призмы ослаблен по сравнению с пучком, падающим на первую призму. 49. На сколько процентов уменьшается интенсивность света после прохождения через призму Николя, если потери света составляют 10%? 50. Угол падения e1 луча на поверхность стекла равен 60°. При этом отраженный пучок света оказался максимально поляризованным. Определить угол e2 преломления луча. 51. Угол преломления луча в жидкости i 2=35°. Определить показатель преломления п жидкости, если известно, что отраженный пучок света максимально поляризован. 52. Угол a между плоскостями пропускания поляроидов равен 50°. Естественный свет, проходя через такую систему, ослабляется в п =8 раз. Пренебрегая потерей света при отражении, определить коэффициент поглощения k света в поляроидах. 53. Пучок света, идущий в стеклянном сосуде с глицерином, отражается от дна сосуда. При каком угле e падения отраженный пучок света максимально поляризован? 54. Пучок света переходит из жидкости в стекло. Угол падения e1 пучка равен 60°, угол преломления e2=50°. При каком угле падения eB пучок света, отраженный от границы раздела этих сред, будет максимально поляризован? 55. Пучок света падает на плоскопараллельную стеклянную пластину, нижняя поверхность которой находится в воде. При каком угле падения eB свет, щаженный от границы стекло—вода, будет максимально поляризован? 56. Частица движется со скоростью v = с /3, где c — скорость света в вакууме. Какую долю энергии покоя составляет кинетическая энергия частицы? 57. При какой скорости b (в долях скорости света) релятивистская масса любой частицы вещества в п =3 paза больше массы покоя? 58. Определить отношение релятивистского импульса электрона с кинетической энергией T =1,53 МэВ к комптоновскому импульсу m o c электрона. 59. Скорость электрона v =0,8 с (где с — скорость света в вакууме). Зная энергию покоя электрона в единицах МэВ, определить в тех же единицах кинетическую энергию Т электрона. 60. Протон имеет импульс р =469 МэВ/с. Какую кинетическую энергию необходимо дополнительно сообщить протону, чтобы его релятивистский импульс возрос вдвое? (1 МэВ/с=5,33х10-22 кг м/с) 61. Во сколько раз релятивистская масса m электрона, обладающего кинетической энергией Т =1,53 МэВ, больше массы покоя m o? 62. Какую скорость b (в долях скорости света) нужно сообщить частице, чтобы ее кинетическая энергия была равна удвоенной энергии покоя? 63. При какой скорости v релятивистская масса частицы в k =3 раза больше массы покоя этой частицы? 64. Релятивистский электрон имел импульс р 1 =т o c. Определить конечный импульс этого электрона (в единицах т o c), если его энергия увеличилась в n =2 раза. 65. Определить скорость v электрона, имеющего кинетическую энергию Т =1,53 МэВ. 66. Релятивистский протон обладал кинетической энергией, равной энергии покоя. Определить, во сколько раз возрастет его кинетическая энергия, если его импульс увеличится в п =2 раза. 67. Электрон движется, со скоростью v =0,6 с, где с — скорость света в вакууме. Определить релятивистский импульс р электрона. 68. Вычислить истинную температуру Т вольфрамовой раскаленной ленты, если радиационный пирометр показывает температуру T рад=2,5 кК. Принять, что поглощательная способность для вольфрама не зависит от частоты излучения и равна a =0,35. 69. Вычислить энергию, излучаемую за время t =1 мин с площади S =l см2 абсолютно черного тела, температура которого T =1000 К. 70. Черное тело имеет температуру Т 1=500 К. Какова будет температура Т 2 тела, если в результате нагревания поток излучения увеличится в п =5 раз? 71. Длина волны, на которую приходится максимум энергии излучения абсолютно черного тела, lm=0,6 мкм. Определить температуру Т тела. 72. Температура абсолютно черного тела Т =2 кК. Определить длину волны lm, на которую приходится максимум энергии излучения, и спектральную плотность энергетической светимости (rl,T)maxдля этой длины волны. 73. Определить максимальную спектральную плотность (rl,T)max энергетической светимости, рассчитанную на 1 нм в спектре излучения абсолютно черного тела. Температура тела Т =1 К. 74. Определить температуру Т и энергетическую светимость Re абсолютно черного тела, если максимум энергии излучения приходится на длину волны lm=600 нм. 75. Из смотрового окошечка печи излучается поток Фе =4 кДж/мин. Определить температуру Т печи, если площадь окошечка S =8 см2. 76. Поток излучения абсолютно черного тела Фе =10 кВт. Максимум энергии излучения приходится на длину волны lm=0,8 мкм. Определить площадь S излучающей поверхности. 77. Как и во сколько раз изменится поток излучения абсолютно черного тела, если максимум энергии излучения переместится с красной границы видимого спектра (lm1=780 нм) на фиолетовую (lm2=390 нм)? 78. Определить поглощательную способность а серого тела, для которого температура, измеренная радиационным пирометром, T рад=1,4 кК, тогда как истинная температура Т тела равна 3,2 кК. 79. Муфельная печь, потребляющая мощность Р =1 кВт, имеет отверстие площадью S =100 см2. Определить долю h мощности, рассеиваемой стенками печи, если температура ее внутренней поверхности равна 1 кК. 80. Средняя энергетическая светимость R поверхности Земли равна 0,54 Дж/(см2 мин). Какова должна быть температура Т поверхности Земли, если условно считать, что она излучает как серое тело с коэффициентом черноты а =0,25? 81. Определить энергию e, массу m и импульс р фотона с длиной волны l=1,24 нм. 82. Красная граница фотоэффекта для цинка lo=310 нм. Определить максимальную кинетическую энергию T max фотоэлектронов в электрон-вольтах, если на цинк падает свет с длиной волны l=200 нм. 83. На поверхность калия падает свет с длиной волны l=150 нм. Определить максимальную кинетическую энергию T max фотоэлектронов. 84. Фотон с энергией e=10 эВ падает на серебряную пластину и вызывает фотоэффект. Определить импульс р, полученный пластиной, если принять, что направления движения фотона и фотоэлектрона лежат на одной прямой, перпендикулярной поверхности пластин. 85. На фотоэлемент с катодом из лития падает свет длиной волны l=200 нм. Найти наименьшее значение задерживающей разности потенциалов U min, которую нужно приложить к фотоэлементу, чтобы прекратить фототок. 86. На пластину падает монохроматический свет (l=0,42 мкм). Фототок прекращается при задерживающей разности потенциалов U =0,95 В. Определить работу А выхода электронов с поверхности пластины. 87. Какова должна быть длина волны излучения, падающего на платиновую пластину, чтобы максимальная скорость фотоэлектронов была v max=3 Мм/с? 88. На цинковую пластину падает пучок ультрафиолетового излучения (l=0,2 мкм). Определить максимальную кинетическую энергию T max и максимальную скорость v max фотоэлектронов. 89. На металлическую пластину направлен пучок ультрафиолетового излучения (l=0,25 мкм). Фототок прекращается при минимальной задерживающей разности потенциалов U min=0,96 В. Определить работу выхода А электронов из металла. 90. Определить максимальную скорость v max фотоэлектрона, вырванного с поверхности металла g-квантом с энергией e=1,53 МэВ. 91. На поверхность металла падает монохроматический свет с длиной волны l=0,1 мкм. Красная граница фото эффекта lo = 0,3 мкм. Какая доля энергии фотона расходуется на сообщение электрону кинетической энергии? 92. На металл падает рентгеновское излучение с длиной волны l=1 нм. Пренебрегая работой выхода, определить максимальную скорость v max фотоэлектронов. 93. На металлическую пластину направлен монохроматический пучок света с частотой n=7,3 1014 Гц. Красная граница lo фотоэффекта для данного материала равна 560 нм. Определить максимальную скорость v maxфотоэлектронов. 94. На цинковую пластину направлен монохроматический пучок света. Фототок прекращается при задерживающей разности потенциалов U =1,5 В. Определить длину волны l света, падающего на пластину. 95. Определить угол q рассеяния фотона, испытавшего соударение со свободным электроном, если изменение длины волны при рассеянии Dl=3,63 пм. 96. Фотон при эффекте Комптона на свободном электроне был рассеян на угол q=p/2. Определить Импульс р (в МэВ/с), приобретенный электроном, если энергия фотона до рассеяния была e1=1,02 МэВ (1 МэВ/с=5,33х10-22 кг м/с). 97. Рентгеновское излучение (l=1 нм) рассеивается электронами, которые можно считать практически свободными. Определить максимальную длину волны lmaxрентгеновского излучения в рассеянном пучке. 98. Фотон с энергией e1, равной энергии покоя электрона (т о с 2 ), рассеялся на свободном электроне на угол q=120°. Определить энергию e2 рассеянного фотона и кинетическую энергию Т электрона отдачи (в единицах т о с 2). 99. Какая доля энергии фотона приходится при эффекте Комптона на электрон отдачи, если рассеяние фотона происходит на угол q=p/2? Энергия фотона до рассеяния e1=0,51 МэВ. 100. Определить максимальное изменение длины волны (Dl)max, при комптоновском рассеянии света на свободных электронах и свободных протонах. 101. Фотон с длиной волны l1=15 пм рассеялся на свободном электроне. Длина волны рассеянного фотона l2=16 пм. Определить угол q рассеяния. 102. Фотон с энергией e1=0,51 МэВ был рассеян при эффекте Комптона на свободном электроне на угол q=180°. Определить кинетическую энергию T электрона отдачи. 103. В результате эффекта Комптона фотон с энергией e1=1,02 МэВ рассеян на свободных электронах на угол q=150°. Определить энергию e1 рассеянного фотона. 104. Определить угол q, на который был рассеян квант с энергией e1=1,53 МэВ при эффекте Комптона, если кинетическая энергия электрона отдачи T =0,51 МэВ. 105. Фотон с энергией e1=0,51 МэВ при рассеянии на свободном электроне потерял половину своей энергии. Определить угол рассеяния q. 106. Определить импульс ре электрона отдачи, если фотон с энергией e1=1,53 МэВ в результате рассеяния на свободном электроне потерял 1/3 своей энергии. | ||
|
| Поделиться: |

 ,
,
 ,
, ,
,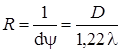 ,
, ,
,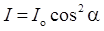
 (в твердых телах),
(в твердых телах), (в растворах),
(в растворах),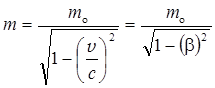 ,
, ,
, — энергия покоя частицы.
— энергия покоя частицы. ,
, .
. .
.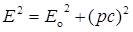
 ,
,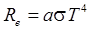 ,
, ,
, ,
,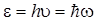 ,
,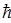 — постоянная Планка, деленная на 2p; n — частота фотона; w — циклическая частота.
— постоянная Планка, деленная на 2p; n — частота фотона; w — циклическая частота.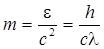 .
.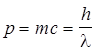 .
.
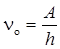 , или
, или 
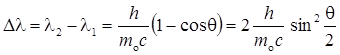 ,
, .
. ,
,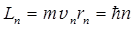 ,
, ,
,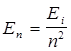 ,
, ,
,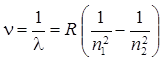 ,
,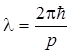 ,
, при v << c (нерелятивистский случай),
при v << c (нерелятивистский случай), при v £ c (релятивистский случай),
при v £ c (релятивистский случай), (для координаты и импульса),
(для координаты и импульса),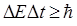 (для энергии и времени),
(для энергии и времени), ,
, ,
, .
.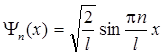 (собственная нормированнаяволновая функция);
(собственная нормированнаяволновая функция); (собственное значение энергии),
(собственное значение энергии),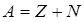 ,
, , или
, или 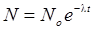 ,
, .
. .
. .
. .
. ,
,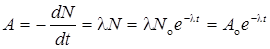 ,
,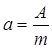 .
. ,
,
 ,
,


