
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Теорема единственности решения теплопроводностиСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Умножим на
Уравнение Бесселя
Разделим на х
Решение будем искать в виде
Коэффициенты с нечетными номерами
Коэффициенты с четными номерами
-Функция Бесселя Общее решение:
Полином Лежандра
Для
Ортогональная система Разложение по ортогональному базису Уравнения эллиптического типа. Уравнение Лапласа на плоскости
Решением u(x, y) являются гармонические функции
Уравнение эллиптического типа
P,q,f – заданные функции
Оператор Лапласа в полярных координатах
Решение уравнения Лапласа в круге
На границе
Оператор Лапласа в цилиндрических координатах
Оператор Лапласа в сферических координатах
Стационарное распределение температуры в сферическом кольце
Перфая формула Грина
G – область n – единичная нормаль
Вторая формула Грина
Следствие
Тогда 1 формула Грина будет
Задача на собственные значение
Свойства L
Такие операторы называются эрмитовыми (сыойство симметричности)
Тогда
Множество значений оператора L Теорема 1 Множество собственных значений оператора L счетно и не имеет конечных предельных точек Теорема 2 Каждое собственное число имеет конечную потреюность, соответствующие им собственные им функции можно выбирать ортоганальными Ткорема 3 Всякая ф-я удовлетворяющая граничным условиям и дтфференцируема, разлагается в сходящийся ряд Фурье косвенными ыункциями оператора L
34
Удовлетворяют условиям
Частный случай оператора L
Линейная ф-я является гармонической в G
Теорема. Принципмаксимумов Если функция u(x) ≠const –Гармоническая в G и D в G –ограниченная область то
В неограниченной области теоремаа не верна
Док во пусть
Это возможно если
Если
Первая краевая задача.Единственность решения
Тогда пусть
В Силу теоремы принципа максимумов u(x) достигает максимума на границе – S Из Следстивие Если ДУ эллиптического вида
Задача в море
Это ф-ла пуассона Задача Дирихле в пространстве. Метод функций Грина
Задача Дирихле
Формула грина для шара A,A*- сопряженные точки
Решение задачи дирихле
Задача Дирихле
Док во
Не завити от e поэтому e можно устремить к 0
Следствие Решение задачи Дирихле в шаре
Решение уравнения Пуссона
Док во
Какаято теорема Пусть
|
|||||||||||||||||||
|
Последнее изменение этой страницы: 2017-01-23; просмотров: 434; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.140.207.29 (0.009 с.) |





 – решение задачи
– решение задачи




 и проинтегрируем по х
и проинтегрируем по х





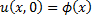













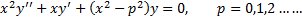

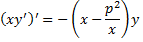
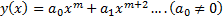


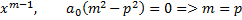






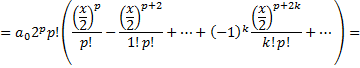







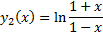





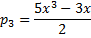














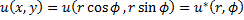
























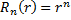



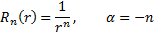




















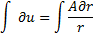










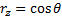




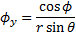



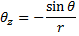

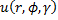










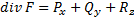


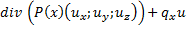




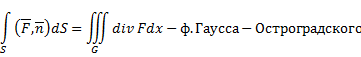



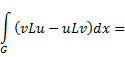







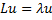





















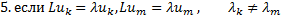




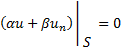

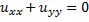






















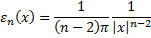

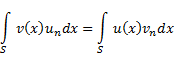







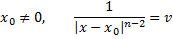





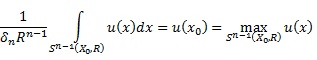

 хотя бы в одной точке то среднее значение
хотя бы в одной точке то среднее значение

 – решения задачи
– решения задачи










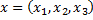


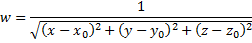





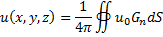





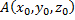



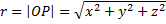
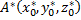







 - гармогическая функция
- гармогическая функция






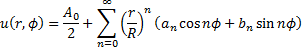




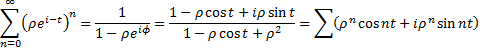








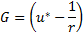
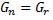



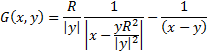


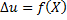
















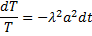

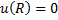





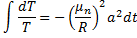








 тогда
тогда




