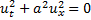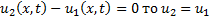Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Вывод уравнения распространения теплаСодержание книги
Поиск на нашем сайте
|n|=1 внешняя единичная нормаль U(x,t) – температура реды в т x (x1,x2 x3) в t
С(х) – удельная теплоемкость K(x) – коэффициент теплопроводности F(x) – интенсивность источника тепла в х в t Производная по направлению – скалрное произведение градиента на нормаль
Закон Фурье Через поверхность S в объем V поступает в промежуток времени [t, t+dt] количество тепла
Составим уравнение баланса тепла
Q2 – тепло которое возникает внутри за счет самого источника Q1 – отток тепла через границу
Изменение температуры u(x,t) за время dt равно u(x, t+dt) – u(x,t) По т. Лагранжа
На это затрачивается количество тепла
Q2 – Забирание тепла извне Q2 – кол во внутреннего тепла Q1 + Q2 - Q3 = 0
V – стягиваем в точку Всилу произвольности V =>
Уравнение теплопроводности
Однородные интегральные уравнения
2 общих интеграла, 2 независимых решения
Примечание
Неоднородные уравнения
Находим частные производные по x
Обратно Пусть функция
Доказать
Док во
И
ДУ гиперболического типа u(x,y,z,t)
f – внешние силы. u – отклонение частицы пр-ва от положения равновесия u(x,y,z,t) -?
Волновое уравнение (q=0, p =a2)
Упрощенный вариант гиперболического уравнения
если известны нач возмущения то известна начальная скорость
Формула Кирхгофа x =x(x1,x2,x3) y=y(y1,y2,y3) x-y < at
Гиперболические уравнения 1 типа
1 Краевая задача
2 Краевая задача
Параболические уравнения Уравнение диффузии и теплопроводности
Задана начальная температура
Формула Пуассона
Уравнения эллиптического типа Отсутствует зависимость от времени (стационарные процессы)
1 Задача Дирихле
2 Задача
3 Уравнения гиперболического типа. Формула даламбера. Имеется бесконечная струна
Вывод Сделаем замену
Уравнения гиперболического типа. Формула Даламбера с внешним воздействием.
Пусть
Уравнения колебаний струны бесконечной справа
Первая краевая задача для конечной струны. Метод Фурье.
Ищем решение в виде
Вторая краевая задача
Колебания струны в среде с сопротивлением m - коэффициент сопротивления среды
1 краевая
Решение краевых задач колебания струны при наличии внешних сил.
Будем искать решение в виде
Случай неоднородных граничных условий.
Делаем замену
19 Теорема единственности решения 1 краевой задачи
u1, u2 – решения данной задачи
Умножим на
По т. Лагранжа
|
||||
|
Последнее изменение этой страницы: 2017-01-23; просмотров: 336; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.119 (0.009 с.) |


 плотность среды
плотность среды

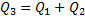
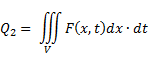
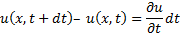



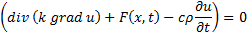

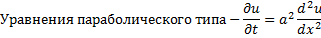

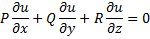
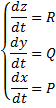
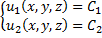

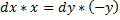
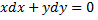 –уравнение с разделяющимися переменными
–уравнение с разделяющимися переменными




 – решение 1.
– решение 1.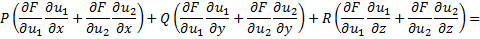
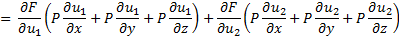


 -решение
-решение -
-  при условии
при условии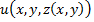



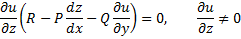
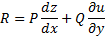
 такая, что функциональное уравнение
такая, что функциональное уравнение 





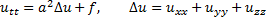


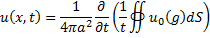







 - заданные функции
- заданные функции



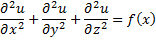




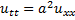


























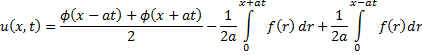
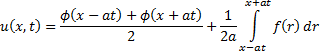






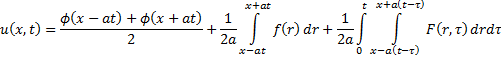


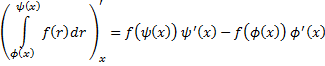
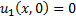 - 1 условие выполнено
- 1 условие выполнено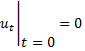 - 2 условие выполнено
- 2 условие выполнено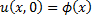



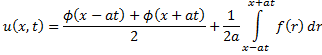




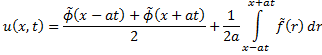























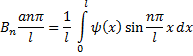


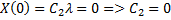
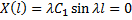
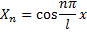
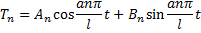

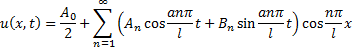







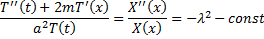






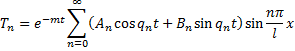
















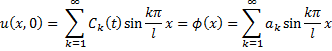
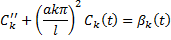






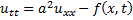











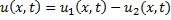

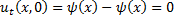
 и проинтегрируем по х
и проинтегрируем по х