
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Уравнения фильтрации для трещинно-пористой средыСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
В чисто трещинном пласте система уравнений имеет тот же вид, что и в пористом. Для трещинно-пористой среды следует учитывать её характерные особенности: 1) моделирование связано с порами разных масштабов (среда 1 – роль поровых каналов играют трещины, а роль зёрен – пористые блоки; среда 2 – обычная пористая среда, образующая блоки); 2) между отмеченными средами при фильтрации возникает переток жидкости из пористых блоков в трещины в пределах выделенного элементарного объёма трещинно-пористого пласта. При этом предполагается, что в каждом элементарном объёме трещинно-пористого пласта содержится большое число пористых блоков, так что в окрестности каждой точки вводится две скорости фильтрации, два давления, относящиеся к средам 1 и 2. На основании сказанного, уравнения неразрывности выписываются для каждой из сред, а переток учитывается членом q1,2. Наличие перетока эквивалентно существованию внутренних источников жидкости в выделенном объёме. Для жидкости, находящейся в трещинах, имеем:
Для жидкости в пористых блоках
Здесь q1,2 – масса жидкости, поступающей из пористых блоков в трещины за единицу времени на единицу объёма (размерность МL-3T-1, где М – размерность массы, L – расстояния и Т – времени). Будем полагать, что q1,2 пропорционально разности фильтрационных потенциалов первой и второй сред q1,2 =Q (j2 - j1),(2.35) где Q – коэффициент переноса, размерности L-2. Для чисто трещинного пласта считаем q1,2=0 и тогда будем иметь только одно уравнение неразрывности для жидкости в системе трещин (в пористых блоках не содержится жидкость). При установившейся фильтрации жидкости в трещинно-пористом пласте, когда во всём пласте существует только одно давление р1=р2=р, получаем
Для чисто трещинного пласта
Начальные и граничные условия
Выше было показано, что уравнения фильтрации сводятся к одному уравнению второго порядка относительно потенциала. В связи с этим, рассмотрим начальные и граничные условия для данного уравнения.
Начальные условия
j = jо (x,y,z) при t = 0, (2.38) если при t = 0 пласт не возмущён, тоj = jо = const. Граничные условия
Число граничных условий равно порядку дифференциального уравнения по координатам. Граничные условия задаются на границах пласта (внешние) и на забое скважины (внутренние). А) Внешняя граница Г 1)постоянный потенциал j (Г,t)= j к=const, (2.39) т.е. граница является контуром питания; 2) постоянный переток массы через границу G = F r `u = const, т.е. используя уравнение (2.30),
3) переменный поток массы через границу
4) замкнутая внешняя граница
5) бесконечный пласт limx®¥ j (Г,t) = j к = const. ( 2.43) у®¥ В) Внутренняя граница 1) постоянный потенциал на забое скважины, радиуса rc j (rc, t)= j c=const; (2.44) 2) постоянный массовый дебит (при условии выполнения закона Дарси)
3) переменный потенциал на забое j (rc,t)=f2(t) при r=rc;(2.46) 4) переменный массовый дебит
5) неработающая скважина
Замыкающие соотношения
Для полного замыкания системы уравнений фильтрационного течения необходимо знание зависимостей r, m, k, μ от давления.
|
||
|
Последнее изменение этой страницы: 2016-12-30; просмотров: 548; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.214 (0.007 с.) |

 . (2.33)
. (2.33)
 . (2.34)
. (2.34) (2.36)
(2.36) . (2.37)
. (2.37)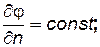 (2.40)
(2.40) (2.41)
(2.41) (2.42)
(2.42) или
или при r=rc; (2.45)
при r=rc; (2.45) при r=rc; (2.47)
при r=rc; (2.47) при r=rc. (2.48)
при r=rc. (2.48)


