
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Неустановившаяся фильтрация газа в пористой средеСодержание книги
Поиск на нашем сайте Уравнение Лейбензона Лейбензон Л.С. получил дифференциальное уравнение для определения давления в пласте при неустановившемся движении в нем идеального газа. Для получения требуемого уравнения используем изотермическое приближение и, следовательно, используем уравнение состояния в виде
Потенциальная функция, как уже отмечалось ранее, имеет вид
Обозначив р2=Р и проделав преобразования общего уравнения нестационарной фильтрации, получим уравнение Лейбензона:
По внешнему виду уравнение (4.37) не отличается от уравнения пьезопроводности (4.11), но множитель перед лапласианом переменен. В связи с этим уравнение (4.37) нелинейно в отличие от линейного уравнения пьезопроводности упругой жидкости и аналитически решается приближенно. Для получения приближенного решения используется метод линеаризации, а именно, переменное давление р заменяется на некоторое постоянное: Лейбензон предложил замену на рк (начальное давление в пласте); Чарный – на рср=рmin+0,7(pmax-pmin), где pmax и pmin – максимальное и минимальное давление в пласте за расчетный период. При указанных допущениях решение будет иметь такой же вид, что и в случае упругой жидкости, но при этом в данных решениях давлению р будет соответствовать Р=р2, æ – æ/ = Таким образом, изменение давления при нестационарной фильтрации газа описывается соотношением
При малых значениях r2/(4 æ/ t) можно заменить интегрально-показательную функцию логарифмической
Формулы (4.38),(4.39) определяют при фиксированных значениях времени распределение давления вокруг газовой скважины, работающей с постоянным дебитом с момента t =0. Депрессионные кривые идентичны кривым при установившейся фильтрации – имеют максимальную кривизну вблизи скважины (рис.4.9а). Если задать значение r, то можно найти изменение давления в данной точке с течением времени (рис.4.9b). В частности, можно найти давление на забое (при r=rc) после начала работы скважины. Уравнение (4.39) используется для расчета коллекторских параметров газовых пластов методом обработки кривой восстановления давления. Принцип расчета такой же, что и в случае нефтяных скважин, но для получения линейной зависимости по оси ординат надо откладывать не депрессию, а разность квадратов пластового и забойного давлений.
ОСНОВЫ ТЕОРИИ ФИЛЬТРАЦИИ МНОГОФАЗНЫХ СИСТЕМ
|
|||
|
Последнее изменение этой страницы: 2016-12-30; просмотров: 470; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.5 (0.008 с.) |

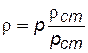 . (4.35)
. (4.35)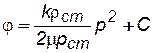 . (4.36)
. (4.36) . (4.37)
. (4.37)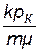 ,
, 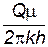 –
– 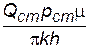 .
.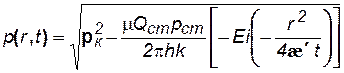 . (4.38)
. (4.38)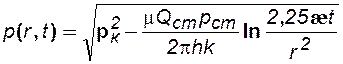 . (4.39)
. (4.39)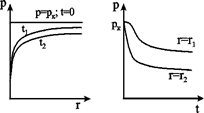 a b
Рис. 4.9. Пьезометрические кривые при неустановившемся притоке газа к скважине в разные моменты времени (а) и изменение давления с течением времени в фиксированных точках пласта (b)
a b
Рис. 4.9. Пьезометрические кривые при неустановившемся притоке газа к скважине в разные моменты времени (а) и изменение давления с течением времени в фиксированных точках пласта (b)



