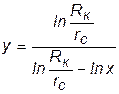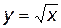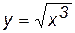Влияние радиуса скважины на её производительность

 

Определим дебит в двух крайних случаях: по закону Дарси – первое слагаемое в формуле (3.33) и по закону Краснопольского развитого нелинейного течения – второе слагаемое. То же самое сделаем и в случае радиально–сферического течения. Если примем радиус одной скважины r_с, а другой – r_c^/ = x^.r_c и, соответственно, дебиты G и G^/, а их отношение обозначим через у = G/G^/, то получим следующие формулы для вычисления предельных значений у

Из таблицы видно, что при сохранении закона Дарси в плоскорадиальном потоке влияние радиуса скважины на дебит невелико (необходимо увеличение радиуса в 10 раз, чтобы дебит вырос на 20%). Если же фильтрация нелинейна, то влияние r_c на G усиливается. Для радиально-сферического потока дебит скважины зависит от радиуса в большей степени, особенно при нелинейном законе фильтрации. При торпедировании забоя, гидравлическом разрыве пласта и других способах воздействия на призабойную зону, образуются и расширяются трещины, что способствует нарушению закона Дарси и, следовательно, усилению влияния радиуса скважины на приток к ней жидкости.

Закон	Тип потока
фильтрации	плоскорадиальный	радиально-сферический
Дарси		у=х
Краснопольского

ВОПРОСЫ ДЛЯ САМОПРОВЕРКИ

1. Какие потоки называются одномерными?

2. Прямолинейно-параллельный поток. Примеры.

3. Плоскорадиальный поток. Примеры.

4. Радиально-сферический поток. Примеры.

5. Что входит в исследование фильтрационного течения.

6. Общее дифференциальное уравнение потенциального одномерного потока.

7. Показатель формы потока.

8. Получение выражения для потенциала и дебита плоскорадиального течения.

9. Получение выражения для потенциала и дебита прямолинейно-параллельного и радиально-сферического течений.

10. Потенциал несжимаемой жидкости в недеформируемом (пористом) пласте.

11. Потенциал несжимаемой жидкости в деформируемом (трещинном) пласте.

12. Потенциал упругой жидкости в недеформируемом пласте.

13. Потенциал сжимаемой жидкости (газа) в недеформируемом (пористом) пласте.

14. Уравнение Дюпюи.

15. Коэффициент продуктивности. Размерность.

16. Депрессия и воронка депрессии.

17. Методика получения закона движения частиц жидкости.

18. Методика вывода средневзвешенного давления.

19. Индикаторная зависимость и индикаторная диаграмма.

20. Нарисовать и объяснить графики давления, скорости фильтрации для несжимаемой жидкости в пористом и трещинном пластах.

21. Нарисовать и объяснить графики давления, скорости фильтрации для несжимаемой жидкости и газа в пористом пласте.

22. Нарисовать и объяснить индикаторные диаграммы для несжимаемой жидкости в пористом и трещинном пластах. В каких координатах надо строить диаграммы, чтобы получить прямолинейные зависимости.

23. Нарисовать и объяснить индикаторные диаграммы для несжимаемой жидкости и газа в пористом пласте. В каких координатах надо строить диаграммы, чтобы получить прямолинейные зависимости.

24. Соотношение дебитов реального и совершенного газов при одинаковых условиях.

25. Принципиальное отличие зависимости для дебита упругой жидкости от несжимаемой.

26. Отличие уравнений притока и дебита для несжимаемой жидкости, текущей по закону Дарси и по двухчленному закону.

27. Зависимость величины проницаемости от метода обработки индикаторной диаграммы.

28. Слоистая неоднородность. Зональная неоднородность.

29. Эффективная проницаемость квазиоднородного пласта при слоистой неоднородности.

30. Эффективная проницаемость прямолинейно-параллельного течения квазиоднородного пласта при зональной неоднородности.

31. Эффективная проницаемость плоскорадиального течения квазиоднородного пласта при зональной неоднородности.

32. Характер изменения дебита и давления в случаях слоистой и зональной неоднородностях.

33. Характер влияния изменения проницаемости призабойной зоны на дебит в случае течения по закону Дарси и нелинейной фильтрации.

34. Виды несовершенств скважины. Совершенная скважина.

35. Приведенный радиус. Относительное вскрытие.

36. Радиус зоны влияния несовершенств по степени и характеру вскрытия.

37. Влияние радиуса скважины на её производительность при линейной и нелинейной фильтрации и различных типов одномерного течения.