
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Система относительных единиц при расчетах КЗСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Выражение электрических величин в относительных единицах широко применяется в теории электрических машин. Это обусловлено тем, что представление любой величины не в именованных, а относительных единицах существенно упрощает теоретические выкладки и придает результатам расчета большую наглядность. Достоинства системы относительных единиц: 1) не нужно следить за обозначениями; 2) позволяет выбрать удобные для расчета числа; 3) основа теории подобия позволяет связать задачи поля с задачами расчета цепей:
Тогда: Под относительным значением какой-либо величины следует понимать ее отношение к другой одноименной величине, принятой за базисную:
Следовательно, перед тем как представить какие-либо величины в относительных единицах, надо выбрать базисные единицы. За базисный ток и базисное линейное напряжение принимаются произвольные величины Iб, Uб. Тогда базисная мощность трехфазной цепи будет определяться формулой:
а базисное сопротивление:
Отсюда вытекает, что только две базисные величины могут быть выбраны произвольно, а остальные являются связанными. Обычно выбирается
единицах при выбранных базисных условиях будут вычисляться по формулам:
Здесь U, I, S, Z − параметры в именованных единицах. При расчетах токов КЗ приняты размерности расчетных параметров к В, к А, МВ·А, М Вт, Мвар, Ом. При этом все формулы не требуют дополнительных согласующих коэффициентов. При задании паспортных данных оборудования в относительных единицах их параметры относят к номинальным параметрам элементов:
Так, относительное сопротивление при номинальных условиях показывает относительное падение напряжения на элементе при протекании номинального тока, что придает физическую наглядность параметру:
При расчетах в системе относительных единиц исходные параметры обычно задаются либо в именованных единицах (и.е.) либо в относительных единицах (о.е.) при номинальных условиях элемента. При построении расчетных схем замещения требуется их перевод в относительные единицы при базисных условиях с обязательным приведением параметров на основную ступень.
При этом для построения расчетных формул требуется решение двух задач: 1) заданы параметры в и.е. − требуется их перевод в о.е. при базисных условиях с приведением на основную ступень; 2) заданы параметры в о.е. при номинальных условиях − требуется их перевод в о.е. при базисных условиях с приведением на основную ступень. Рассмотрим порядок построения расчетных формул на примере сопротивлений и ЭДС. 1) Заданы
Здесь:
Формулы (4.17) и (4.18) являются формулами точного приведения. При приближенном приведении
где При обычно используемом условии
2) Заданы
Здесь Формулы (4.22) и (4.23) являются формулами точного приведения. При приближенном приведении
При обычно используемых условиях
В дальнейшем индекс приведения будет опускаться. 4.4. Определение сопротивления элементов электрических систем Формулы определения сопротивлений приведены в относительных единицах при приближенном приведении к базисным условиям. Генераторы. У генераторов практически никогда не учитывается активное сопротивление, так как оно пренебрежительно мало по сравнению с индуктивным. Номинальное сопротивление генератора в относительных единицах − − − Номинальное сопротивление генератора в относительных единицах при базисных условиях определяется формулой: Двигатели. Параметры синхронных электродвигателей определяются аналогично генераторам. Реакторы. Токоограничивающие реакторы могут иметь различное устройство и конструктивное исполнение, а также технические и технико-экономические характеристики и параметры.
Линейные реакторы, включаемые последовательно в соответствующую линию, ограничивают ток КЗ и поддерживают относительно высокий уровень остаточного напряжения. Сопротивление линейного реактора можно определить по формуле:
Сдвоенный реактор обладает лучшими характеристиками. Между ветвями реактора существует магнитная связь, которая в сквозном режиме позволяет уменьшить потери напряжения в реакторе. Коэффициент магнитной связи идентичных ветвей обмотки реактора равен:
Сдвоенный реактор имеет 3 режима работы (рис. 4.11) Одноцепный режим (рис. 4.11а). В одноцепном режиме общее сопротивление реактора определятся как сопротивление одной его ветви:
а) б) в) Рис. 4.11. Режимы работы сдвоенного реактора Двухцепный (сквозной) режим (рис. 4.11б). Двухцепный режим – это нормальный режим работы реактора. В таком режиме магнитные потокиветвейнаправлены встречно, что вызывает уменьшение индуктивного сопротивления одной ветви. Индуктивное сопротивление одной ветви: Общее индуктивное сопротивление: Продольный режим (рис. 4.11в). В продольном режиме магнитные потоки ветвейнаправлены согласно и индуктивность ветви увеличивается.
Каждый режим работы реактора может быть представлен своей схемой замещения. Активное сопротивление обычно не учитывается, но оно может быть найдено по потерям активной мощности в реакторе. На рисунке 3 приведена общая схема замещения сдвоенного реактора.
Рис. 4.12. Обозначение сдвоенного реактора и его схема замещения Рассмотрим пример. Используя схему замещения (рис. 4.12), определим сопротивление реактора в одноцепном, сквозном и продольном режимах. Коэффициент связи равен В режиме КЗ (одноцепном):
В нормальном (сквозном) режиме:
В продольном режиме:
Трансформаторы
Рис. 4.13. Условное обозначение и схема замещения двухобмоточного трансформатора
Параметры схемы замещения производятся по данным опытов холостого хода и короткого замыкания.
Потери холостого хода:
Сопротивление холостого хода:
Рис. 4.14. Опыт холостого хода
Опыт короткого замыкания (рис. 4.15) позволяет определить напряжение короткого замыкания и потери короткого замыкания:
Напряжение короткого замыкания Рис. 4.15. Опыт короткого замыкания
Потери короткого замыкания:
Активное сопротивление трансформатора: Пренебрегая ветвью намагничивания
Рис. 4.16. Схема замещения
Активное сопротивление трансформатора в относительных единицах, приведенное к базисным условиям:
где
Рис. 4.17. Условное обозначение и схема замещения трёхобмоточного трансформатора
В относительных единицах напряжения короткого замыкания обмоток будут равняться их сопротивлениям рассеивания и их значения для обмоток высшего, среднего и низшего напряжений трехобмоточного трансформатора могут быть определены по формулам:
Данные формулы справедливы и для автотрансформатора, Трансформатор с расщепленной обмоткой. На электростанциях и подстанциях применяются силовые трансформаторы и автотрансформаторы с расщепленной обмоткой низшего напряжения, так как это позволяет существенно снизить ток КЗ в сетях низшего напряжения. Повышающие трансформаторы и автотрансформаторы с расщепленной обмоткой используются для формирования укрупненных блоков электростанций, особенно на ГЭС.
а) б) Рис. 4.18 Условное обозначение трансформатора с расщепленной обмоткой: а) обмотка низшего напряжения расщеплена на 2 части; б) обмотки низшего напряжения расщеплена на 3 части
Сопротивление трансформатора с расщепленной обмоткой характеризуется следующими параметрами: − сопротивление расщепления − сквозное сопротивление − коэффициент расщепления
а) б) в) г)
Рис. 4.19 Схемы замещения трансформатора с расщепленной обмоткой
Сопротивление рассеивания обмоток трансформатора:
При расщеплении низшей обмотки на 2 части (рис. 4.19а) сопротивление обмоток низшего напряжения:
Сопротивление обмотки высшего напряжения:
Для трансформатора стрежневого типа и При расщеплении низшей обмотки на 3 части (рис. 4.19г) сопротивление обмотки высшего напряжения: Сопротивление обмоток низшего напряжения:
Пример. Автотрансформатор с расщепленной обмоткой низшего напряжения на 2 части (рис. 4.20). Сопротивление расщепленных обмоток низшего напряжения:
Сопротивления обмоток высшего, среднего и низшего напряжений:
Рис. 4.20. Автотрансформатор с расщепленной обмоткой и его схема замещения
|
|||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-12-27; просмотров: 559; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.216.128.55 (0.01 с.) |

 ;
;  ;
;  ;
;  , где
, где  ,
, ;
;  ;
;  .
.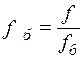 . (4.10)
. (4.10) , (4.11)
, (4.11) . (4.12)
. (4.12) и Uб. Причем выбранные базисные величины должны быть едиными для всей расчетной схемы и применяться как к полным величинам, так и к их отдельным составляющим. Следовательно, параметры электрической системы в относительных
и Uб. Причем выбранные базисные величины должны быть едиными для всей расчетной схемы и применяться как к полным величинам, так и к их отдельным составляющим. Следовательно, параметры электрической системы в относительных ;
;  ;
;  ; (4.13)
; (4.13) ;
; 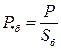 ;
;  ; (4.14)
; (4.14)

 . (4.15)
. (4.15) ;
; 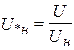 ;
;  ;
; 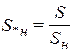 ;
;  . (4.16)
. (4.16) .
.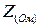 ,
,  .
. 
 (4.17)
(4.17)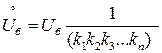 − базисное напряжение, приведенное на расчетную ступень.
− базисное напряжение, приведенное на расчетную ступень. (4.18)
(4.18) ; (4.19)
; (4.19)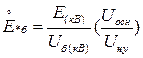 , (4.20)
, (4.20) − номинальное напряжение ступени, где установлен элемент.
− номинальное напряжение ступени, где установлен элемент. формулы принимают вид:
формулы принимают вид: ;
;  . (4.21)
. (4.21) ,
,  .
.  (4.22)
(4.22) . (4.23)
. (4.23) − номинальное паспортное напряжение элемента.
− номинальное паспортное напряжение элемента. (4.24)
(4.24) (4.25)
(4.25)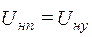 формулы принимают вид:
формулы принимают вид:
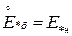 . (4.26)
. (4.26) может быть определено из паспортных данных:
может быть определено из паспортных данных: ,
,  − синхронные сопротивления по продольной и поперечной оси, которые характеризуют установившийся режим.
− синхронные сопротивления по продольной и поперечной оси, которые характеризуют установившийся режим. и
и  ,
, 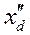 и
и  − переходные и сверхпереходные сопротивления в момент времени t = 0.
− переходные и сверхпереходные сопротивления в момент времени t = 0.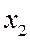 ,
, 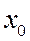 − сопротивления обратной и нулевой последовательностей.
− сопротивления обратной и нулевой последовательностей. .
. , где
, где  лежит в пределах 0,1…0,4 Ом.
лежит в пределах 0,1…0,4 Ом. .
.



 .
. .
. .
.

 0,5.
0,5. .
. .
. .
. Двухобмоточный трансформатор. Схема замещения двухобмоточного трансформатора приведена на рисунке 4.13.
Двухобмоточный трансформатор. Схема замещения двухобмоточного трансформатора приведена на рисунке 4.13.
 Опыт холостого хода (рис. 4.14) позволяет определить ток холостого хода
Опыт холостого хода (рис. 4.14) позволяет определить ток холостого хода  , потери в ветви намагничивания
, потери в ветви намагничивания  и сопротивление холостого хода.
и сопротивление холостого хода.
 ;
;  .
.
 , следовательно, индуктивное сопротивление рассеивания определяется как
, следовательно, индуктивное сопротивление рассеивания определяется как  .
. .
.

 , получим упрощенную схему замещения (рис. 4.16):
, получим упрощенную схему замещения (рис. 4.16):

 ,
, − номинальное активное сопротивление в относительных единицах.
− номинальное активное сопротивление в относительных единицах. Трехобмоточный трансформатор
Трехобмоточный трансформатор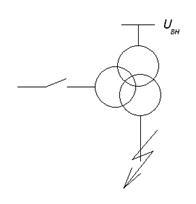
 ,где
,где  ;
; 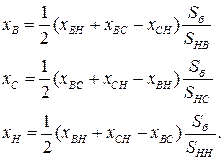

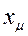 обычно в расчеты не вводится.
обычно в расчеты не вводится.

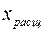 , равное сопротивлению между выводами двух произвольных частей расщепленной обмотки;
, равное сопротивлению между выводами двух произвольных частей расщепленной обмотки;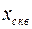 , равное сопротивлению между выводами обмотки высшего напряжения и объединенными выводами частей расщепленной обмотки низшего напряжения;
, равное сопротивлению между выводами обмотки высшего напряжения и объединенными выводами частей расщепленной обмотки низшего напряжения; , равный отношению сопротивления расщепления к сквозному сопротивлению:
, равный отношению сопротивления расщепления к сквозному сопротивлению:
 При расщеплении обмотки на две части
При расщеплении обмотки на две части 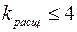 (рис. 4.18а), а при расщеплении на три части
(рис. 4.18а), а при расщеплении на три части  (рис. 4.18б). Коэффициент расщепления также зависит от исполнения трансформатора, например, для трансформатора броневого исполнения (рис. 4.18а) при отсутствии других данных следует принимать
(рис. 4.18б). Коэффициент расщепления также зависит от исполнения трансформатора, например, для трансформатора броневого исполнения (рис. 4.18а) при отсутствии других данных следует принимать  . Для группы однофазных трансформаторов
. Для группы однофазных трансформаторов  .
.





 схемы замещения для активных и индуктивных сопротивлений приведены на рис. 4.19б, в.
схемы замещения для активных и индуктивных сопротивлений приведены на рис. 4.19б, в. .
.







