
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Логикой называют науку о закономерностях в связях и развитии мыслей.Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Как самостоятельная наука она сложилась более 2000 лет назад в IV в. до н. э. Одним из основателей является древнегреческий философ Аристотель. В своих логических трудах, получивших общее название «Органон» - (греч. «орудие познания»), Аристотель сформулировал основные законы мышления: § тождества § непротиворечия § исключенного третьего Он описал важнейшие логические операции, разработал теорию понятия и суждения, исследовал дедуктивное (силлогизм) умозаключения. Его учения продолжили Гален, Порфирий и др. Примерно в это же время логика развивается в философских трудах мыслителей Китая, Индии, Тибета, Индонезии. Логика развивалась и в средние века, применительно к религиозной схоластике. Значительны успехи логической науки в Новое время, толчком для которой послужило развитие промышленного производства, науки, рост духовного производства. Важнейшим этапом в развитии логики явилась теория индукции, разработанная английским философом Ф. Бэконом (1561-1626) в книге «Новый Органон». В своем труде он докладывает принципиально новое отношение к логике. Если раньше логику рассматривали как искусство ведения диспутов, то автор «Нового Органона» утверждает, что логика инструмент познания. Ф. Бэкон говорит о важности объективности в познании, точности в речи, освобождении этого процесса от эмоций, пристрастности, влияния устаревших авторитетов. Индукция, по Бэкону, помогает найти причину вещей. Он разработал методы определения причинной связи между явлениями, роль эксперимента в научном познании и многое другое. Дальнейшее развитие логики связано с именами таких мыслителей как Р. Декарт, Г. Лейбниц, И. Кант и др. Р. Декарт (1569-1650) выступил с критикой средневековой схоластики. Он развил идеи дедуктивной логики, сформулировал правила научного исследования, изложенного в сочинении «Правила для руководства ума». В 1662г. вышла книга «Логика или искусство мыслить», написанная последователями Р. Декарта, А. Арно и П. Николем, известная под названием «Логика Пор-Рояля». Крупный вклад в исследования логических проблем внес немецкий философ Г. Лейбниц (1646-1716), сформулировавший закон «Достаточного основания», выдвинувший идею математической логики, которая получила развитие лишь в XIX-XXв.в. Значительные заслуги в развитии логики И. Канта, М.В. Ломоносова, С.И. Поварнина. Во второй половине XIX в. в логике начинают широко применятся разработанные в математике методы исчисления. Это направления разрабатывается в трудах Д. Буля, У. Джевонса, П. Порецкого, Б. Рассела, Я. Лукасевича. Теоретический анализ дедуктивных рассуждений методами исчисления с использованием формализованных языков получил название математической или символической логики.
Диалектическая логика. Принципы диалектической логики были сформулированы Гегелем (1770-1831). Диалектическая логика изучает законы развития человеческого мышления, а также методологические принципы и требования, которые формируются на их основе. К ним относятся объективность и всесторонность рассмотрения предмета; принцип историзма; раздвоение единого на противоположные стороны; восхождения от абстрактного к конкретному; принцип и единство исторического и логического в познании и др. Формальная логика как наука о формах мыслей. Формальная логика изучает формы мышления, выявляет структуру, общую для различных по содержанию мыслей. Она изучает законы, обуславливающие логическую правильность мышления, без соблюдения которой нельзя прийти к результатам, соответствующим действительности, познать истину. Мы будем изучать формальную логику с элементами символической (математической) логики. Язык логики. Материальным носителем мысли является язык, речь. Различают устную и письменную речь, языки естественные и искусственные – специальные. Логика исследует формы мыслей, способы их выявления и выражения в языке. В связи с этим в логике изучаются отдельные аспекты естественных языков, а также создаются искусственные языки – язык логики высказываний, символическая логика, логика предикатов и др. При логическом анализе язык рассматривается как система знаков. Знак – материальный чувственно-воспринимаемый объект, который символически, условно представляет и отсылает обозначенному им предмету, явлению, действию или событию, сигнализирует о предмете, явлении или свойстве и т.п., который им обозначается. Выделяют знаки трех типов: (1) знаки – индексы; (2) знаки – образы; (3) знаки – символы. Логика исследует знаки - символы, которые не связаны материально и не уподобляются им по форме т внешнему виду. В современной логике общепринятым является язык логики предикатов. Основными семантическими категориями языка являются: имена предметов, имена признаков, предложения. Имя предмета – это отдельные слова или словосочетания обозначающие предметы. Каждое имя имеет всегда двойное значение – предметное и смысловое. Предметное значение – это объект, который обозначается этим знаком. Такими объектами могут выступать: предметы, явления, действия, отношения и др. («стол», «погода», «поступление»). Смысловое значение – информация, которую несет имя о предмете, о свойствах, признаках, на основании которых выделяют предмет или их множество: «деревянный стол», «осенняя погода», «наступление армии». Различают имена простые, не включающие других имен («территория»), сложные – включающие другие имена («территория парка»). Имя может быть единичным – обозначать один предмет («Луна», «Киев», «Эльбрус», «Эверест»). В речи он чаще всего представлен именем собственным или дается описательно: («спутник Земли», «высочайшая вершина Альп», «столица Украины»). Общее имя – обозначает множество, содержащее больше одного предмета: («группа», «полк», «государство»). Основной формой выражения логической мысли служит повествовательное предложение, в котором с помощью имен, логических знаков выражается истина или ложь.
Виды знаков (символов): 1. a, b, c… - символы для единичных (собственных или описательных) имен предметов (a – Сидоров, b – Иванов, c – Петров); 2. x, y, z… - символы общих имен (студент, учащийся, академик - x, y, z…); 3. p, q, r … - символы для высказываний; 4. " - «все» («каждый») – квантор общности $ - «некоторые», «иногда» - квантор существования 5. Логические связки: ù - «неверно, что», «не» - знак отрицания &, Ú - «и» - конъюнкция – знак объединения Ù - «или» - дизьюнкция – знак разделения ®, É - «если…то» - импликация, знак условности º -«если и только если…то» - знак эквивалентности, тождества двойное условие (…) – скобки (,) – занятая круги Эйлера Пример: «Иванов, Сидоров, Петров – студенты академии. (а, b, с)"х.у. «Если я сдам сессию (а) и буду свободна (b), то поеду отдыхать в Крым (с) или на Кавказ (с,). (аÙb)®(сÚùс,). Упражнения. Ответьте на контрольные вопросы: 1. Что такое знак? 2. Основные виды знаков? 3. Что такое имя? Основные виды имен? Приведите примеры. 4. Поставьте запятую в предложении: «Казнить нельзя помиловать» С помощью логических знаков выразите: @ «Видеть несправедливость и молчать - это значит самому участвовать в ней» @ «И добродетель стать пороком может, когда ее неправильно приложат» (У. Шекспир) @ «Если больному после разговора с врачом не становится легче, то это не врач» (Бехтерев В.М.) Литература: А.Д. Гетманова Логика М., 1986 с 16-25; А.Є. Конверський Логіка К. 1998, с 34-83
Занятие 2.
Понятие Понятие как вид мысли. Важнейшими видами мыслей, в которых отражается действительность в процессе абстрактного мышления, является понятие. Понятие – форма логической мысли, представляющая собой результат обобщения предметов или явлений по их существенным признакам. В понятии диалектически синтезируется целостный образ на основе существенных отличительных признаков предметов или явлений. Признак - это наличие или отсутствие у предмета свойств или отношений, характеризующих предмет. Пример: «Часть суши, окруженная со всех сторон водой» «Глубокая, узкая горная долина с практически отвесными скалами» «Отсутствие демократии в государстве» Понятие неразрывно связано со словом, называемым в логике именем. Важнейшими характеристиками понятий является содержание и объем. Содержание и объем понятий, класс. Содержание – это система признаков на основе осуществлено обобщение и выделение предмета. Пример: Геометрическая, прямоугольная фигура с равными сторонами: - «квадрат» Объем – множество обобщаемых и выделяемых предметов в понятии. Соотношение между содержанием и объемом понятий определяется законом обратного отношения, согласно которому с увеличением содержания уменьшается объем понятия и наоборот. Сравните: 1. «Город» - общее понятие с ограниченным содержанием. 2. «Город, который является столицей государства» 3. «Столичный город Франции» - понятие с меньшим объемом, но большим содержанием. Виды понятий. табл. №1
Литература: А.Д. Гетманова Логика М., 1986 с 25-31; А.Є. Конверський Логіка К. 1998, с 129-141
Упражнения. 1) Укажите единичные и общие понятия, определите, какие общие понятия являются регистрирующими, подчеркните собирательные понятия: · Днепропетровская область · Бригада морской пехоты · Рабочий класс · Организация объединенных наций · Наука · Молодежь, студент, студент Иванов · Юридическое лицо
2) Укажите конкретные и абстрактные понятия: политическая система, преступность, диктатура, двуличие, трезвость, Родина, противоречие, спутник, бездорожье, белизна. 3) Укажите положительные и отрицательные понятия: верность, безволие, ненависть, анархия, ананас, гуманизм, антиквар, халатность, беспорядок, принципиальность, контроль. 4) Выясните, являются ли данные понятия безотносительными или соотносительными: причина, рабочий, вверх, политика, ускорение, копия, положение, проблема, право, племянник, практика. 5) Дайте полную логическую характеристику понятиям: государство, академия, кража, невменяемость, чертеж, бескорыстие, талант. Пример: «Государство» - понятие общее, не регистрирующее, положительное, безотносительное. Отношение между понятиями. Отношения между понятиями – принято изображать кругами Эйлера. Понятия по отношению друг к другу делятся на сравнимые и не сравнимые. В логических отношениях могут находиться только сравнимые, совместимые понятия, которые делятся на: 1) равнообъемные 2) пересечение, перекрещивание 3) подчинение
Пример: a) равнообъемность: «А» - премьер министр; «В» - глава правительства
- по объему и содержанию эти понятия совпадают
b) пересечение: «А» - студент, «В» - спортсмен
c) подчинение: «А» - академия, «В» - факультет, «С» -факультет
Понятия, объемы которых не совпадают ни полностью, ни частично называют несовместимыми. Они содержат признаки, исключающие совпадения их объемов. Три вида отношений не совместимости: 1) соподчинения (координация)
2) противоположности (контрарности) – понятия содержат несовместимые признаки пример: студент – А, отличник – В, неуспевающий – С.
3) противоречия (контрадикторности) – отношение понятий содержащих взаимоисключающие признаки пример: черный – белый, отрицательный – положительный заряд электронов, производство «А» - потребление «В»
Упражнения. Определите вид отношения между совместимыми понятиями и изобразите его с помощью круговых схем Эйлера. Высшее учебное заведение, университет. Юрист, депутат парламента. Конница, кавалерия. Орган государственного управления, министерство. Писатель, украинский писатель, автор повести «Тарас Бульба». Республика, форма правления. Президент, президент США, глава государства. Художник, живописец, Левитан. Офицер, орденоносец, спортсмен. Литератор, прозаик, поет. Ученый, сторонник мира, гражданин Швеции. Мать, дочь, родители. Операции над понятиями. Методы образования понятий 1. Анализ – мысленное расчленение предмета на составляющие его признаки; 2. Сравнение - установление сходства либо различия между рассматриваемыми предметами; 3. Синтез – мысленное соединение различных признаков предмета в единое целое; 4. Абстрагирование – выделение отдельных признаков, составляющих содержание понятий из всей совокупности признаков предмета; 5. Обобщение – действие абстрагирования и обобщения неразрывно связаны; Обобщение и ограничение понятий Обобщить понятие – значит, перейти от понятия с меньшим объемом, но большим содержанием к понятию с большим объемом, но меньшим содержанием. Ограничить понятие – значит, перейти от понятия с большим объемом, но меньшим содержанием к понятию с меньшим объемом, но с большим содержанием. Пример: – обобщения понятия: «Теория государства и права» - юриспруденция «Ректор» - руководитель вуза Пример: – ограничения понятия: «Великая держава» - Китай «Религия» - Буддизм «Организм» - растение
Упражнения. Обобщите понятия Конституция. Повесть. Антарктида. Осень. Пропаганда войны. Рыночное хозяйство. Министр. Верховный суд автономной республики Крым. Ограничьте понятия Революция. Закон. Форма мышления. Республика. Политическая партия. Учебник. Созвездие. Культура. Проверьте правильность обобщения понятий Кабинет министров – правительство Лето – наиболее теплое время года Халатность – должностное преступление Договор – сделка Районный жилмассив - микрорайон Род – племя Проверьте правильность ограничения понятия Государство – республика Классовое общество – общественный класс Организм – живая клетка Оркестр – виолончель Старший офицер – майор Циферблат – цифра Общественная организация – профсоюз Политическое движение – борьба за мир Литература: А.Д. Гетманова Логика М., 1986 с 36-69; А.Є. Конверський Логіка К. 1998, с 141-169.
Занятие 3. Суждение Строение суждения. Суждение – форма мысли, в которой утверждается или отрицается что-либо относительно предметов и явлений, их свойств, связей и отношений, и которая обладает свойством выражать истину, либо ложь. Пример: Маркетинг – деятельность по созданию спроса на товары и услуги (в том числе PR – реклама, мерчендайзинг, научные исследования по изучению спроса имеющегося и создания нового спроса) Та часть суждения, которая отображает предмет мысли, называется субъектом (лат. subjectum) суждения и обозначается латинской буквой S. Это подлежащее суждение. Та часть суждения, которая отображает то, что утверждается (или отрицается) о предмете мысли, т.е. субъекте, называется предикатом (лат. praedicatum) суждения и обозначается латинской буквой P. Предикат отображает наличие или отсутствие того или иного признака у предмета и является сказуемым суждения. В нашем примере субъект выражен словом «маркетинг», а предикат словами «система функций капитала по реализации товаров». Элемент суждения, который соединяет субъект и предикат называется связка. Связка выражена словом «есть». Суждение можно изобразить символически в виде такой формулы: S есть (не есть) Р. Языковой формой суждения является повествовательное предложение. Вопросительные и побудительные предложения ничего, не утверждая и не отрицая, не обладают значением истинности и суждений не выражают. Пример: «Прощай, свободная стихия!» (Пушкин А.С.) – побудительное предложение, суждения не выражает. «Кто сегодня отсутствует?» - вопросительное. Упражнение. Найдите предложения, выражающие суждения 1. Кто автор сочинения «Новый Органон»? 2. Всякое преступление – противоправное деяние. 3. Нет повести печальнее на свете, чем повесть про Ромео и Джульетту. 4. Мой друг! Отчизне посвятим души прекрасные порывы! (А.С. Пушкин) 5. Ни один подложный документ не является доказательством. 6. Кооператив вправе принимать любые решения, если это не противоречит действующему законодательству. 7. Одни поддельные цветы дождя боятся. 8. Подготовьтесь к зачету!
В зависимости от объема и содержания, отображаемых в суждении предметов и характера связи предметов и свойств суждения можно разделить их несколько видов. По качеству отображаемых предметов суждения делятся на утвердительные и отрицательные. Пример: Аренда не есть форма собственности. Всякий человек имеет право на жизнь, свободу, личную неприкосновенность. (Всеобщая декларация прав человека) По объему или количеству отображаемых предметов суждения делятся на единичные, частные, общие. Пример: «Лев Толстой не писал стихов», «Некоторые писатели в молодости писали стихи», «Все писатели – художники слова». Отвлекаясь от конкретного содержания данных частных суждений, можно установить, что структура у всех подобных суждений одинакова. Она выражается следующей формулой: некоторые S суть (или не суть) Р. В символической логике частное суждение называется суждением существования и выражается формулой $ х A (х), т.е. «существует или не существует такой то Х, для которого выполняется А(х), или ù А (х). Частные суждения бывают утвердительными и отрицательными и называются частноутвердительными и частноотрицательными. Пример: «Некоторые иностранные фирмы имеют украинских сотрудников», «Несколько служащих не довольны своим окладом». В логике приняты обозначения буквами А, Е, О, I виды суждений: А - общеутвердительное суждение; Е – общеотрицательное суждение; О – частно-отрицательное суждение; I – частно-утвердительное суждение. Пример: 1. Каждый гражданин имеет право на образование – А; 2. Ни один нацистский преступник не уйдет от наказания – Е; 3. Некоторые страны имеют однопартийную систему – I; 4. Некоторые страны не имеют морских границ – О.
Упражнения. Дайте объединительную классификацию суждений, используя обозначения: А, Е, О, I. 1. Некоторые сделки являются односторонними. 2. В этой деревне огни не погашены. (Рубцов). 3. Не все выдающиеся музыканты имели абсолютный слух. 4. В здоровом теле здоровый дух. 5. Каждый профессиональный футболист имеет свой уровень мастерства. 6. Сделка, направленная на ограничение прав человека, не является законной. 7. Маршал Жуков – выдающийся полководец второй мировой войны. 8. Ничто не проходит бесследно. 9. Никакая поддержка банд террористов не может быть оправдана. Суждения могут быть простыми и сложными. Простыми называются суждения, в которых нельзя выделить часть, которая сама являлась бы суждением. Простые суждения подразделяются на атрибутивные суждения, суждения об отношениях и суждения существования. Атрибутивные суждения - выражает принадлежность каких либо свойств предметам или отсутствие у них таковых. Пример: «Некоторые имена не являются общими – О» «Логика – философская наука» - А «Дельфины - не рыбы» - Е Атрибутивные суждения делятся на виды по качеству и количеству. По качеству они делятся на утвердительные и отрицательные. По количеству – на единичные, частные и общие. Пример: «Все горючие сланцы – полезные ископаемые» - А «Некоторые вирусы болезнетворные» - I Атрибутивное суждение определяется еще и как категорическое суждение, в котором выражается знание о принадлежности или непринадлежности признака предмету независимо от каких либо условий. Пример: «Рыбы дышат жабрами» «Киты не принадлежат к рыбам» Суждения об отношениях В этих суждения утверждается наличие или отсутствие определенного отношения между элементами предметов. Пример: Киев севернее Одессы. Петров учится лучше Иванова. Человек не живет два века. Везувий – действующий вулкан близ Неаполя. Простыми являются также суждения существования «Инопланетяне существуют», суждения тождества – (а=b) «Жизнь – это существование белковых тел». Упражнения. Определите вид суждений: 1. В атмосфере Юпитера нет кислорода. 2. Зима этого года теплее зимы 2002 года. 3. Каждая страна имеет свой гимн. 4. Законность – неотъемлемая часть демократии. 5. В музее находится одна из последних работ художника. 6. Книга природы есть неисчерпаемый источник знания. (Вольтер) 7. Не существует абсолютной повторяемости явлений. 8. Лишь тот достоин жизни и свободы, кто каждый день идет за них на бой. (Гете).
Модальность суждений. В практике человеческого мышления встречаются суждения, в которых оценивается характер утверждаемой связи между субъектом и предикатом. Модальность – (от лат. modus - способ) – это явно или неявно выраженная дополнительная информация о степени достоверности отображенного фактора, явления – от вероятности до необходимости существования отображаемого, и его оценка. В структуру модельных суждений входит оператор, позволяющий оценивать характер связи между субъектом и предикатом, выражающийся обычно парными категориями: «хорошо – плохо», «необходимо – случайно», «доказано – опровергнуто» и др. Структура модельных суждений М (S есть Р), или М (S не есть Р), где М означает модальный оператор (модальное понятие). В формальной логике суждения по модульности делятся на эпистемическую, деонтическую, алетическую. Эпистемическая («эпистема» - греч. означает умозрительный или интеллектуально- созерцательный тип достоверного значения) модульность это выраженная в суждении информация об основаниях принятия того или иного решения, мнения, факта. По степени обоснования различают достоверные и проблематичные суждения. Пример: «Хорошо, что студенты добросовестно относятся к учебе» (достоверное). «Вероятно, добросовестные студенты успешно сдадут сессию» (проблематично). Деонтическая (от греч. «деонтическая» - обязанность) модальность – это выраженное в суждении предписание в форме совета, пожелания, приказа, побуждающее человека к конкретным действиям. К деонтическим относятся различного рода нормативные высказывания, правила, рекомендации. Пример: «Запрещается переходить улицу на красный свет» «Студенты обязаны сдавать экзамены в срок» «Каждый гражданин Украины имеет право на защиту своей жизни и здоровья» Алетическая (по-гречески означает «истинный») модальность – это выраженная в терминах необходимости – случайности либо возможности- невозможности информация о детерминированности суждения или факта. Логическая модальность характеризует истинность или ложность структуры или формы суждения. Истинными являются суждения, построенные в соответствии с законами логики и отвечающие истинности факта действительности. Алетическая модальность используется при формировке законов, теоретических выводов. Пример: «Эйфелева башня находится в Париже» «Сумма углов треугольника равна 180о» «Кислород необходим для поддержания жизни» Сложные суждения. Сложные суждения образуются из простых с помощью логических связок. В соответствии с функциями логических связок различают: 1) Соединительные - (конъюнктивные) суждения, состоящие из нескольких простых, связанных логической связкой «и». « Все люди рождаются свободными и равными в своем достоинстве», - сложное суждение. Его можно изобразить символически: Р – все люди рождаются свободными, - первое суждение. q – все люди рождаются равными в своем достоинстве – второе суждение Р Ù q Ù- символ конъюнкции Соединительное суждение истинно при истинности всех составляющих его конъюнктов и ложно при ложности хотя бы одного из них. Условия истинности суждения рÙq показаны в таблице, где истинность обозначена – и, а ложность - Ù Таблица №1
Упражнение Приведите примеры, подтверждающие истинность распределений суждений в данной таблице. 2) Разделительный (дизъюнктивные) суждения состоят из нескольких простых, связанных логической связкой «или» «Ú» Пример: «Оскорбление может быть нанесено либо случайно, либо намерено». Это предложение может быть представлено в виде двух простых суждений: «Оскорбление может быть нанесено случайно» - р «Оскорбление может быть нанесено намерено» - ġ
Нестрогая и строгая дизъюнкция Нестрогая дизъюнкция - суждение, в котором связка «или» употребляется в соединительно-разделительном значении (символ Ú). Пример: «По форме правления современное государство может быть республикой или монархией» Связка «или» в данном случае и разделяет, поскольку существует как государства- республики, так и государства – монархии, и соединяет, т.к. существуют государства, которым присущи черты как первого, так и второго. Суждение р Ú q будет истинным при истинности хотя одного члена дизъюнкции. Дизъюнкция будет ложной при ложности обоих ее членов.
Таблица №2 Упражнение. Проверьте на примерах правильность данной таблицы. Строгая дизъюнкция – суждение, в котором связка «или» употребляется в разделительном значении. В этих суждениях утверждается наличие одной из двух и более ситуаций. Члены строгой дизъюнкции, называемые альтернативами, не могут быть одновременно истинными. Пример: «Паду ли я стрелой пронзенный, (р) ( (
Условия истинности и строгой дизъюнкции представлены в табл. 3
Упражнения. Подберите примеры, иллюстрирующие справедливость данной таблицы. Практический совет В некоторых случаях, когда требуется четко выразить мысль, например при заключении договора, важно не только употреблять союз «или», но и пояснить дополнительно, что утверждается наличие (или возможность) двух ситуаций или же только одной из них. Так, отечественная фирма заключила договор с иностранной фирмой на поставку сырья взамен оргтехники. В договоре на русском языке было сказано, что отечественная фирма получает оргтехнику, а взамен поставляет уголь или нефть. Подразумевался не разделительный смысл союза «или». При переводе на английский язык был употреблен союз «or», а не выражение «or»(and), как это принято в тех случаях, когда требуется указать на соединительно-разделительный смысл союза «или». Фирма расплатилась частично углем, а частично нефтью. Пришлось заплатить неустойку, поскольку арбитражный суд признал претензии иностранной фирмы справедливыми. 3) Условные (импликативные) суждения состоят из двух простых суждений, связанных логической связкой «ЕСЛИ…ТО». Связка обозначается знаком ®. Пример: «Если я видел дальше других (р), то потому, что стоял на плечах гигантов». (q) Таблица №4
Символически суждение можно выразить р®q Первый член импликации (или антецедент), называется еще основанием, второй (или консеквент) называется следствием.
Таблица истинности для импликативных суждений выглядит как это показано в таблице №4.
4) Суждение эквивалентности В суждениях эквивалентности утверждается взаимная обусловленность двух ситуаций, выражаемая посредством предложений с союзом «если и только если, … то» («тогда, и только тогда, … когда»). Союз обозначается символом«. Пример: «Вода в нормальных условиях замерзает (р) тогда и только тогда, когда температура опускается ниже 0оС.(q) Символически это выражение можно изобразить р«q(или º) Выражение читается «р, если и только если q». Таблица истинности для суждений эквивалентности выглядит, как это показано в табл.5. Таблица №5
В суждении эквивалентности, как и в суждении условном можно выделить основания и следствия. Основание в них выражает достаточное и необходимое условие для ситуации, описываемой следствием. Упражнения. Придумайте примеры эквивалентных суждений в соответствии с табл. 5. Отношение между суждениями. При составлении разных точек зрения по спорным вопросам, когда не ясно, кто из спорящих прав, а кто не прав, можно по логическим формам суждений установить, могут ли все спорящие быть правы, или не правы, совместимы ли обсуждение концепций, а если совместимы, то в каких частях. Основу отношений между суждениями составляет их сходство по смыслу и логическим значениям (истинности и ложности), поэтому отношения устанавливаются не между любыми, а лишь между сравнимыми, т.е. имеющими общий смысл суждениями.
Вершины А, Е, О, I – символизирует простые категорические суждения, стороны и диагонали – отношения между суждениями. Среди сравнимых различают совместимые и не совместимые. К совместимым относятся суждения А и I, Е и О, которые одновременно могут быть истинными. Различают 3 вида совместимости: эквивалентность, (полная совместимость), частичная совместимость (субконтрарность) и подчинение. Отношение несовместимости могут быть в суждениях А и Е, О, Е и I, которые одновременно не могут быть истинными. Различают два вида несовместимости: противоположность и противоречивость. Противоположными (контрарными) являются суждения А и Е, которые одновременно не могут быть истинными, но могут быть одновременно ложными. Пример: «Все студенты прошли стажировку на предприятиях города»- А «Никто из студентов не стажировался на предприятиях города» - Е А®ùЕ – одно из них истинно. «Все птицы зимой улетают в теплые края» - А «Ни одна птица не улетает зимой в теплые края» - Е А®ùЕ (оба утверждения ложны) Противоречащими (контрадикторными) являются суждения А и О, Е и I, которые одновременно не могут быть ни истинными, ни ложными. Если А признается истинным, то О будет ложным. (А®ùО), при истинности Е будет ложным I (Е®ù I). И наоборот, при ложности А будет истинным О(ù А®О), а при ложности Е будет истинным I (ùЕ®О). Пример: Если истинным будет суждение «Все люди признают свои ошибки», то ложным будет «Некоторые люди не признают свои ошибки». Контрольные вопросы: 1) В чем различие между простыми и сложными суждениями? 2) Дайте характеристику атрибутивного суждения? 3) Основные виды отношений между суждениями? 4) Какие виды сложных суждений Вы знаете? 5) Что такое модальность суждений?
Упражнение. 1. Приведите примеры простых суждений различных видов (А, Е, О, I) 2. Определите модальность следующих суждений: 3. Ошибочно приписывать современным кибернетическим устройствам способность мышления и тем более сознания. 4. Материя неразрывно связана с движением. 5. Каждый человек имеет право на гражданство. 6. В шесть часов я, вероятно, буду дома. 7. В общественном транспорте запрещается провоз легковоспламеняющихся веществ. 8. Не плюй в колодец – пригодится воды напиться. 9. Вероятно, молоко было одним из первых продуктов сельского хозяйства. 10.Невозможно построить вечный двигатель.
Литература: А.Д. Гетманова Логика М., 1986 с 70-97; А.Є. Конверський Логіка К. 1998, с 170-202
Раздел II.
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-12-26; просмотров: 1523; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.144.108.200 (0.01 с.) |







 ) иль мимо пролетит она». (q)
) иль мимо пролетит она». (q) ) – знак строгой дизъюнкции Таблица №3
) – знак строгой дизъюнкции Таблица №3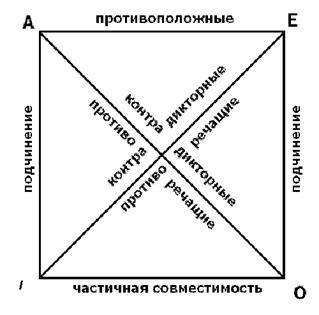 Отношения между простыми суждениями рассматривается с помощью логического квадрата изобретенного византийским логиком М. Пселом.
Отношения между простыми суждениями рассматривается с помощью логического квадрата изобретенного византийским логиком М. Пселом.


