
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Модуль и аргумент комплексного числа. Главное значение аргумента. Тригонометрическая и показательная формы комплексного числа. Действия над комплексными числами в тригонометрической форме.Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Z=a+b A=(a,b) |Z|=r=
Z=r(cos
ArgZ=h –аргумент комплексного числа - |Z|=
z
Пример: Z=4+3i X=4 y=3 >0. 2 четверть |Z|=sqrt(4*4+3*3)=sqrt25=5 Tga=y/x=3/4 a=arctg(3/4)+ПК argZ=arctg(3/4) Z=5*(cos(arctg(3/4))+isin(arctg(3/4))) –тригонометрическая форма. Z=5*e*arctg(3/4) – показательная форма. Действия 1) Умножение 2) Деление 3)Введение в степень
4) извлечение корня из n степени
Корень n-ой степени из комплексного числа. Логарифм и степень комплексного числа.
Sin(x+2пк)=sinx
Приведём главное значение логарифма для некоторых аргументов: Правило Крамера. Решение линейных систем алгебраических уравнений. Если DetA не равен 0, то слау при условии n=m имеет единственное решение. X=DetA/Detb Метод Крамера (правило Крамера) — способ решения квадратных систем линейных алгебраических уравнений с ненулевым определителем основной матрицы (причём для таких уравнений решение существует и единственно) Пример.
A =
x1 = D1/detA; x2 = D2/detA; x3 = D3/detA;
Системы линейных алгебраических уравнений. Общие понятия. Теорема Кронекера-Капелли. Определение. Система m уравнений с n неизвестными в общем виде записывается следующим образом:
где aij – коэффициенты, а bi – постоянные. Решениями системы являются n чисел, которые при подстановке в систему превращают каждое ее уравнение в тождество. Ax=B
Решением слау называется упорядоченный набор чисел х1 х2 х3 при постановке которых в уравнение системы каждый из этих выражений обращается в тождество
Теорема Кронекера-Капелли: Неоднородная слау была совместна, необходима и достаточная, чтобы ранг основной матрицы был равен рангу расширенной матрицы этой систему. 1) Если решение существует, то столбец свободных членов есть линейная комбинация столбцов матрицы А, а значит добавление этого столбца в матрицу, т.е. переход А®А* не изменяют ранга. 2) Если RgA = RgA*, то это означает, что они имеют один и тот же базисный минор. Столбец свободных членов – линейная комбинация столбцов базисного минора, те верна запись, приведенная выше. Однородные и неоднородные системы линейных алгебраических уравнений. Теоремы о существовании решений. Структура общего решения.
Слау называется однородной если В1=В2=Вм=0 Ax=0 Слау называется не однородной если В1, B2, …, Bm не равно 0.
Свойства однородной системы 1* любая однородная слау совместна, имеет решение X1=0 X2=0 Xn=0 2* любая линейная комбинация решений однородной слау является решение этой системы 3* однородная слау имеет не нулевое решение тогда и только тогда когда ранг матрицы её коэффициента меньше количества её неизвестных 4* однородная слау имеет только нулевое решение когда ранг коэффициента равен количеству не известных этой системы.
|
|||||
|
Последнее изменение этой страницы: 2016-12-14; просмотров: 715; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.12.146.108 (0.012 с.) |

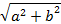

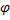 +sin
+sin 

 =cos
=cos  показатель формулы комплексного числа
показатель формулы комплексного числа тригонометрической формой комплексного числа.
тригонометрической формой комплексного числа.

 +isin(xa))
+isin(xa)) - формула Муавра
- формула Муавра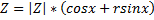


 =|Z|*(
=|Z|*(
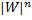 =
= 

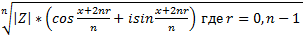

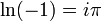
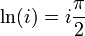


 ; D1=
; D1=  ; D2=
; D2=  ; D3=
; D3=  ;
; , (1)
, (1)


