
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Производная функции. Дифференцирование суммы, разности, произведения и частного двух функций. Геометрический смысл производной функции.Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Производная функции. Дифференцирование суммы, разности, произведения и частного двух функций. Геометрический смысл производной функции. Определение. Производной функции f(x) в точке х = х0 называется предел отношения приращения функции в этой точке к приращению аргумента, если он существует. Производная - основное понятие дифференциального исчисления, характеризующее скорость изменения функции. Определяется как предел отношения приращения функции к приращению ее аргумента при стремлении приращения аргумента к нулю, если таковой предел существует. Дифференцирования суммы: Дифференцирования разности: Дифференцирования произведения (правило Лейбница): Дифференцирования частного:
f(x)
f(x0 +Dx) P Df f(x0) M
a b Dx 0 x0 x0 + Dx x
Пусть f(x) определена на некотором промежутке (a, b). Тогда
где a - угол наклона касательной к графику функции f(x) в точке (x0, f(x0)).
Угол между кривыми может быть определен как угол между касательными, проведенными к этим кривым в какой- либо точке. Уравнение касательной к кривой: Уравнение нормали к кривой: Производные основных элементарных функций. 1)С¢ = 0; 9) 2)(xm)¢ = mxm-1; 10) 3) 4) 5) 6) 7) 8)
Дифференциал функции, его свойства. Определение. Дифференциалом функции f(x) в точке х называется главня линейная часть приращения функции. Обозначается dy или df(x). Из определения следует, что dy = f¢(x)Dx или dy = f¢(x)dx. Можно также записать: Дифференциал функции f – это линейная функция y=f’(x0)*(x-x0) в точке x0 и обозначают df. Для функции x производная в каждой точке равна 1, то есть dx=x-x0 Поэтому пишут: df=f’(x)dx Дифференциал в математике — линейная часть приращения функции или отображения. Приближенное значение функции вблизи точки равно сумме ее значения в этой точке и дифференциала в этой же точке. Это дает возможность записать производную следующим образом: f’(x)=df/dx Геометрически дифференциал функции df – это приращение ординаты касательной к графику функции в данной точке при изменении абсциссы точки на dx. Свойства 1) d(u ± v) = (u ± v)dx = udx ± vdx = du ± dv 2) d(uv) = (uv)dx = (uv + vu)dx = vdu + udv 3) d(Cu) = Cdu 4)
Дифференцирование элементарных функций. Табличные производные.
Дифференцирование элементарных функций 1) (X+Y) ’=X’+Y’ 2) (X-Y) ’=X’-Y’ 3) (C*X) ’=C*X’, Где С это постоянная 4) (X*Y) ’=X’Y+XY’ 5) (X/Y) ’=(X’Y-XY’)/(Y*2) 6) (F(K*X+B)) ’=KF’*(KX+B) ’ 7) (F(g(X)) ’=F’(g(X))*g’ (x)
Табличные производные 1) C’=0, где С постоянная 2) (Xn) ’=n*xn-1 3) 4) (ex)’=ex 5) (Ax)’=Ax*ln g 6) (Ln x)’= 7) (sin x)’= cos x 8) (Cos x)’= - sin x 9) (Tg x)’= 10) (Ctg x)’ = - 11) (Arcsin x) ’= 12) (Arcos x) ’= - 13) (Arctg x) ’= 14) (Arcctg x) ’= -
Операции над матрицами А.Сложение матриц Это сумма матриц А и В одинакового размера MxN, называется квадратные матрицы MxN, которые определяются по формуле Сij=Aij+Bij
Б. умножение матриц Произведение матрицы А размера М и Х называется матрица В размерами М и Х, такая что Вij=P*aij, где Р это любое число.
5*
В. Вычитание матриц Разность А-В матриц элементами ij одинакового размера M и X называется матрица С размерами М и Х такая что Cij=Aij-Bij
Г. Произведение матриц Необходимое условие: количество столбцов матрица А равно количеству строк матрицы В. Произведение матрицы А размерами М х К на матрицу В размерами К и N называется матрица С размерами М и К. такая что Cij=Ai1*B1j+Ai2*B2j+Ai3*B3j…+Aik*Bkj Примеры
A*B= B*A= Свойства 1.) Сложение и вычитание допускается только для матриц одинакового размера. 2.) Существует нулевая матрица Θ такая, что её прибавление к другой матрице A не изменяет A, то есть A + Θ = A 3.) Все элементы нулевой матрицы равны нулю. 4.) Возводить в степень можно только квадратные матрицы. 5.) Ассоциативность сложения: A + (B + C) = (A + B) + C. 6.) Коммутативность сложения: A + B = B + A. 7.) Ассоциативность умножения: A(BC) = (AB)C. 8.) Дистрибутивность умножения относительно сложения: A(B + C) = AB + AC; (B + C)A = BA + CA. 9.) Свойства операции транспонирования матриц: (AT)T = A (AB)T = BTAT (A − 1)T = (AT) − 1, если обратная матрица A - 1 существует. (A + B)T = AT + BT detA = detAT 10.) Умножение матриц не коммутативно, т.е. АВ ¹ ВА даже если определены оба произведения. Однако, если для каких – либо матриц соотношение АВ=ВА выполняется, то такие матрицы называются перестановочными 11.)Если произведение АВ определено, то для любого числа a верно соотношение: a(AB) = (aA)B = A(aB).
Матричный многочлен Пусть f(x)=a0xn+a1xn-1+…+an-1x+an
A – квадратная матрица порядка М F(a)= a0An+a1An-1+…+an-1A+anE Где Е единичная матрица порядка М Называется матричный многочлен степени М Для любой квадратной матрицы А определено произведение А*А. Назовем произведение А*А квадратом матрицы А: A2 = A*A. Произведение A*Ar-1 для любого целого положительного числа r называется r-й степенью матрицы А. Т.е. Ar=A*Ar-1. Обозначаем Ar. Свойства определителей. 1) Если все элементы некоторой строки или столбца равны 0, то определитель равен 0 2) Если определитель имеет 2 одинаковых строки или 2 одинаковых столбца, то он равен 0 3) Если элементы 2 строк пропорциональны то определитель равен 0 4) (Линейная зависимость строк и столбцов) Если все элементы К ого столбца определителя N порядка имеют вид Aij=L1*ai1+L2*ai2+…+Lk1*aik+Lk+1*aik+…+Ln*ain то определитель равен 0 Замечание: имеет место аналогичное свойство для строк
5) При транспортировании матриц определитель не меняется 6) Общий множитель некоторой строки элементов выноситься за знак определителя
7) При перестановке 2 ух строк или 2 ух столбцов определителя изменяется только знак
8) Если в некоторой строке прибавить другую строку умноженную на произвольные числа то определитель не измениться 9) Если к некоторому столбцу прибавить другой столбец умноженный на любое число то определитель не изменится 10) Если все элементы К ого столбца определителя Д n-ого порядка приставить в виде Aij=L1Bi1+L2bi2, то Д=L1Д1+L2Д2 11) Определитель Д ого порядка равен сумме по парных произведений всех элементов I ой строки, на их алгебраические дополнения 12) Определитель треугольной и диагональной матрицы равен произведению всех её элементов главной диагонали 13) det A = det AT; 14) det (A ± B) = det A ± det B. 15) det (AB) = detA×detB
Сложение и вычитание.
Умножение.
В тригонометрической форме:
3) Деление.
В тригонометрической форме:
4) Возведение в степень.
В общем случае получим: 5) Извлечение корня из комплексного числа.
Отсюда:
Свойства однородной системы 1* любая однородная слау совместна, имеет решение X1=0 X2=0 Xn=0 2* любая линейная комбинация решений однородной слау является решение этой системы 3* однородная слау имеет не нулевое решение тогда и только тогда когда ранг матрицы её коэффициента меньше количества её неизвестных 4* однородная слау имеет только нулевое решение когда ранг коэффициента равен количеству не известных этой системы. Полярная система координат
Определение Полярная система координат из точки О на плоскости, называется полюсом, луча, исходящего из полюса и единичного отрезка.
Луч, исходящий из полюса, называется полярным лучом или полярной осью.
Полярными координатам точки А на плоскости являются полярный радиус r и полярный угол
Определение Полярным радиусом точки А называется расстояние от точки А до полюса.
Определение Полярным углом точки А, называется величина ориентированного угла между полярным лучом ОР и углом ОА
Производная функции. Дифференцирование суммы, разности, произведения и частного двух функций. Геометрический смысл производной функции. Определение. Производной функции f(x) в точке х = х0 называется предел отношения приращения функции в этой точке к приращению аргумента, если он существует. Производная - основное понятие дифференциального исчисления, характеризующее скорость изменения функции. Определяется как предел отношения приращения функции к приращению ее аргумента при стремлении приращения аргумента к нулю, если таковой предел существует.
Дифференцирования суммы: Дифференцирования разности: Дифференцирования произведения (правило Лейбница): Дифференцирования частного:
f(x)
f(x0 +Dx) P Df f(x0) M
a b Dx 0 x0 x0 + Dx x
Пусть f(x) определена на некотором промежутке (a, b). Тогда
где a - угол наклона касательной к графику функции f(x) в точке (x0, f(x0)).
Угол между кривыми может быть определен как угол между касательными, проведенными к этим кривым в какой- либо точке. Уравнение касательной к кривой: Уравнение нормали к кривой: Производные основных элементарных функций. 1)С¢ = 0; 9) 2)(xm)¢ = mxm-1; 10) 3) 4) 5) 6) 7) 8)
|
|||||||
|
Последнее изменение этой страницы: 2016-12-14; просмотров: 924; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.143.4.99 (0.012 с.) |





 у
у тангенс угла наклона секущей МР к графику функции.
тангенс угла наклона секущей МР к графику функции.  ,
,
 .
.
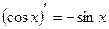
 11)
11) 
 12)
12) 
 13)
13) 
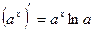 14)
14) 
 15)
15) 
 16)
16) 


 =
= 




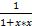

 =
= 
 =
= 



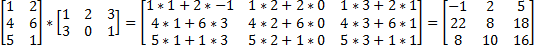
 =0
=0



 ,
, 






 ,
,






