
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Упрощение систем высказыванийСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
До сих пор мы упрощали высказывания в целом. Как быть, если имеется некоторая их система? Упростить систему высказываний значит привести ее к меньшему числу не более сложных высказываний: {А, В, С, D, Е} = {F, G, H} Рассмотрим возможные случаи. 1) С истема истинных высказываний А, В, С, D, Е. Каждое из высказываний данной совокупности истинно, поэтому истинна конъюнкция всех этих высказываний. Чтобы упростить данную систему высказываний, нужно составить конъюнкцию из высказываний А, В, С, D, Е и привести ее эквивалентными преобразованиями к конъюнкции более простого вида: ABCDE = FGH. 2) Система высказываний А, В, С, D, Е, относительно которых известно, что по меньшей мере одно из них истинно. По меньшей мере одно из высказываний А, В, С, D, Е истинно, значит истинна дизъюнкция всех данных высказываний. Поэтому, чтобы упростить данную систему высказываний, нужно составить дизъюнкцию из данных высказываний и привести ее путем эквивалентных преобразований к дизъюнкции более простого вида: А + В + С + D + Е = F + G + H. 3) С истема высказываний А, В, С, D, Е, в которой хотя бы одно из высказываний ложно. Если хотя бы одно из высказываний системы ложно, то ложна и конъюнкция этих высказываний. Поэтому для упрощения данной системы используется конъюнктивная нормальная форма: АВСDЕ = FGH. 4) Система ложных высказываний А, В, С, D, Е. Если все высказывания системы ложны, то ложна и их дизъюнкция. Поэтому для упрощения данной системы используется дизъюнктивная нормальная форма: А + В + С + D + Е = F + G + H.
Решение логических задач Законы логики высказываний могут быть использованы при решении логических задач, условия которых представляют собой совокупность высказываний, по которым требуется установить истинность или ложность других высказываний. Фактически решение логической задачи сводится к правильному преобразованию ее условия по законам логики. Оно включает ряд этапов: 1) формализовать условие задачи; 2) составить систему высказываний, т.е. объединить условие в единую формулу; 3) путем эквивалентных преобразований привести формулу к искомому результату.
Рассмотрим следующую задачу. Кто из студентов-заочников был вчера в библиотеке, если известно следующее: 1. Если в библиотеке Алексеев, то с ним обязательно бывают Борисов и Волков. 2. Если Волков идет в библиотеку, то Григорьев отправляется с ним. 3. Дмитриев бывает в библиотеке тогда и только тогда, когда там Борисов. 4. По крайней мере, Алексеев или Борисов были в библиотеке. 5. Либо Дмитриев, либо Григорьев были вчера в библиотеке. Запишем условия задачи в символической форме, обозначая высказывания буквами в соответствии с фамилиями персонажей. Очевидно, что все условия задачи справедливы одновременно, то есть их конъюнкция тождественно-истинна. 1 Ù 2 Ù 3 Ù 4 Ù 5 = И, где 1: А ® (Б Ù В); 2: В ® Г; 3: Д «Б; 4: А Ú Б; 5: Д Ú Г. Учитывая это, получим следующее соотношение: (А ® (Б Ù В)) Ù (В ® Г) Ù (Д «Б) Ù (А Ú Б) Ù (Д Ú Г) = И Удалим знаки импликации, эквиваленции и строгой дизъюнкции, а в качестве знаков дизъюнкции и конъюнкции выберем для удобства, соответственно, “+” и “·”, тогда будем иметь:
1 2 3 4 5 По правилам алгебры логики перемножим скобки: (1)х(4): (1)х(4)х(3): (1)х(4)х(3)х(5): (1)х(4)х(3)х(5)х(2): Таким образом, получаем Контрольные задания В №№ 501 – 520 определите логическую структуру следующих атрибутивных суждений и приведите их к канонической форме (в необходимых случаях выявите их недостающие – подразумеваемые – смысловые части). Пример. Древние греки внесли большой вклад в развитие философии. Это суждение частноутвердительное. Каноническая форма: Некоторые S есть Р. Некоторые (квантор) древние греки (S) есть (связка) люди, внесшие большой вклад в развитие философии (Р).
501. Ликург – великий законодатель древности. 502. Все сделки, не соответствующие требованиям закона, являются недействительными. 503. Некоторые птицы не летают. 504. Киты не дышат жабрами. 505. Некоторые студенты являются мастерами спорта. 506. Все дороги ведут в Рим. 507. Народ земного шара хочет мира. 508. Все распространенные предложения имеют второстепенные члены. 509. Среди дикорастущих растений многие представляют собой большую ценность для медицины. 510. Человек находится на верхней ступени эволюционной лестницы. 511. Ни одно исключение не опровергает правило. 512. Иногда люди опаздывают на работу. 513. Электроны имеют отрицательный электрический заряд. 514. Жили у бабуси три веселых гуся. 515. В архивах хранятся и закрытые дела. 516. Некоторые выдающиеся математики не приняли неевклидовой геометрии. 517. Имеются приборы, преобразующие ультразвук в звук, слышимый человеком. 518. Ни один ученый не мыслит формулами. 519. Каждый кулик свое болото хвалит. 520. Ни один квадрат не имеет острых углов.
В №№ 521 – 530 составьте возможные истинные суждения вида А, Е, I, О, используя в качестве субъекта и предиката следующие понятия:
521. Крестьянское восстание; восстание, закончившееся победой. 522. Русский феодал; сторонник преобразований Петра I. 523. Комета; тело Солнечной системы. 524. Звезда; мощный источник радиоизлучения. 525. Студент; именной стипендиат. 526. 15; простое число. 527. Домашнее животное; друг человека. 528. Выпускник вуза; работник банка. 529. Президент США; католик. 530. Представитель африканского племени; человек с белым цветом кожи.
В №№ 531 – 545 определите распределенность терминов и выразите отношения между терминами с помощью диаграмм Эйлера-Венна.
531. Некоторые чувства не выразимы в словах. 532. Ни один нейтрон не имеет электрического заряда. 533. В листьях некоторых растений не происходит фотосинтез. 534. Животные семейства кошачьих относятся к классу млекопитающих. 535. Некоторые античные философы были римскими императорами. 536. Ни одно имя собственное не пишется с маленькой буквы. 537. Некоторые разумные советы не применимы на практике. 538. Субъект общего суждения всегда распределен. 539. Некоторые солдаты вовсе не мечтают стать генералами. 540. Ни один студент СГПУ не является лауреатом Нобелевской премии. 541. Некоторая часть новых экспонатов была передана музею. 542. Всего лишь четыре студента 23-й группы не явились на семинар по логике. 543. Ни один вопрос студентов не остался без ответа. 544. Большинство подростков отличаются активным поведением. 545. Люди – не ангелы.
В №№ 546 – 605 запишите символически сложные высказывания, употребляя буквы для обозначения простых компонентов предложения (под простыми компонентами подразумеваются предложения, не содержащие логических связок):
546. Либо я отправляюсь в поездку, либо встречаю гостей. 547. Идет дождь, или кто-то не выключил душ. 548. Если вечером будет туман, то Иван или останется дома, или должен будет взять такси. 549. Иван сядет, и он или Дмитрий будут ждать. 550. Иван сядет и будет ждать, или Дмитрий будет ждать. 551. Я поеду или на автобусе, или на такси. 552. Ни белые, ни красные не победили в гражданской войне. 553. Хлеба уцелеют тогда и только тогда, когда будут вырыты ирригационные канавы, и если хлеба не уцелеют, то фермеры обанкротятся и оставят фермы. 554. Если я устал или голоден, я не могу заниматься. 555. Если Иван встанет и пойдет в школу, он будет доволен, а если он не встанет, он не будет доволен. 556. Сын работает на заводе, а дочь учится в школе. 557. Неверно, что сын не работает на заводе, или дочь не учится в школе. 558. Иван и Петр друг друга не любят. 559. Неверно, что Иван любит Петра, и Петр любит Ивана. 560. Каждый студент этого факультета способен и трудолюбив. 561. Неверно, что каждый студент этого факультета неспособен или нетрудолюбив. 562. Прямоугольные треугольники бывают равнобедренными или неравнобедренными. 563. Неверно, что прямоугольные треугольники бывают равнобедренными и неравнобедренными. 564. Иван либо сын, либо внук Петра. 565. Неверно, что Иван сын Петра тогда и только тогда, когда является его внуком. 566. Если слово ставится в начале предложения, то оно пишется с большой буквы. 567. Неверно, что слово ставится в начале предложения и при этом не пишется с большой буквы. 568. Если по проводнику проходит электрический ток, то вокруг проводника возникает магнитное поле. 569. Если вокруг проводника возникает магнитное поле, то по проводнику проходит электрический ток. 570. Число является четным тогда и только тогда, когда оно делится на два. 571. Если число четное, то оно делится на два, а если число нечетное, то оно не делится на два. 572. Человек нечестен и несправедлив. 573. Неверно, что если человек нечестен, то он справедлив. 574. На улице темно и сыро. 575. Неверно, что на улице не темно или не сыро. 576. Я получаю стипендию тогда и только тогда, когда сдаю экзамены. 577. Я не получаю стипендию тогда и только тогда, когда не сдаю экзамены. 578. Я либо читаю книгу, либо иду в кино. 579. Я либо не читаю книгу, либо не иду в кино. 580. Я тогда и только тогда иду в кино, когда не читаю книгу. 581. Либо я иду в кино, либо читаю книгу. 582. Либо я не читаю книгу, либо я хочу прилечь. 583. Тогда и только тогда я читаю книгу, когда хочу прилечь. 584. Если будет хорошая погода, то мы отправимся в путешествие. 585. Не будет хорошей погоды, или мы не отправимся в путешествие. 586. Я учусь в институте или не работаю на заводе. 587. Если я работаю на заводе, то учусь в институте. 588. Тогда и только тогда мы отправимся в путешествие, когда будет хорошая погода. 589. Будет хорошая погода, и мы отправимся в путешествие, или не будет хорошей погоды, и мы не отправимся в путешествие. 590. Неверно, что тогда и только тогда мы отправимся в путешествие, когда будет хорошая погода. 591. Будет хорошая погода, но мы не отправимся в путешествие, или не будет хорошей погоды, а мы отправимся в путешествие. 592. Либо я увлекаюсь гимнастикой, либо плаванием. 593. Я увлекаюсь гимнастикой, но не увлекаюсь плаванием. 594. Неверно, что либо я увлекаюсь гимнастикой, либо плаванием. 595. Я увлекаюсь гимнастикой и плаванием, или я не увлекаюсь ни гимнастикой, ни плаванием. 596. “Иль чума меня подцепит, иль мороз окостенит, Иль мне в лоб шлагбаум влепит непроворный инвалид” (А. Пушкин). 597. “Что неясно представляешь, то неясно и высказываешь; неточность и запутанность выражений свидетельствует только о запутанности мыслей” (Н. Чернышевский). 598. Новый год он будет встречать либо в Ростове, либо в Москве. 599. Не покупай кота в мешке, если тебе не нужен мешок. 600. “Вода и камень, стихи и проза, лед и пламень не столь различны меж собой” (А. Пушкин). 601. Кто хочет что-нибудь сделать – находит средства, кто не хочет ничего делать – находит оправдания. 602. “Если кто-то из товарищей опаздывал на молебен, или доходили слухи о какой-нибудь проказе гимназистов, или видели классную даму поздно вечером с офицером, то он очень волновался и все говорил, как бы чего не вышло” (А. Чехов). 603. Если я намереваюсь поехать в деревню тогда и только тогда, когда я сдам экзамен, то если я не сдам экзамен, то я останусь в городе. 604. “Пушкин в карты не играл, а если и играл, то без всяких фокусов” (М. Булгаков). 605.
В №№ 606 – 645 установите логически истинностные значения следующих суждений: 606. Конъюнкция высказываний (pÙq) истинна. Что можно сказать о логическом значении дизъюнкции этих высказываний (pÚq)? 607. Конъюнкция высказываний (pÙq) истинна. Что можно сказать о логическом значении импликации этих высказываний (p®q)? 608. Конъюнкция высказываний (pÙq) истинна. Что можно сказать о логическом значении эквиваленции этих высказываний (p«q)? 609. Дизъюнкция высказываний (pÚq) ложна. Что можно сказать о логическом значении импликации этих высказываний (p®q)? 610. Конъюнкция высказываний (pÙq) истинна. Что можно сказать о логическом значении строгой дизъюнкции этих высказываний (p Ú q)? 611. Дизъюнкция высказываний (pÚq) ложна. Что можно сказать о логическом значении эквиваленции этих высказываний (p«q)? 612. Дизъюнкция высказываний (pÚq) ложна. Что можно сказать о логическом значении строгой дизъюнкции этих высказываний (p Ú q)? 613. Импликация высказываний (p®q) ложна. Что можно сказать о логическом значении конъюнкции этих высказываний (pÙq)? 614. Импликация высказываний (p®q) ложна. Что можно сказать о логическом значении дизъюнкции этих высказываний (pÚq)? 615. Импликация высказываний (p®q) ложна. Что можно сказать о логическом значении эквиваленции этих высказываний (p«q)? 616. Импликация высказываний (p®q) ложна. Что можно сказать о логическом значении строгой дизъюнкции этих высказываний (p Ú q)? 617. Дизъюнкция высказываний (pÚq) ложна. Что можно сказать о логическом значении конъюнкции этих высказываний (pÙq)? 618. Эквиваленция высказываний (p«q) ложна. Что можно сказать о логическом значении конъюнкции этих высказываний (pÙq)? 619. Эквиваленция высказываний (p«q) ложна. Что можно сказать о логическом значении дизъюнкции этих высказываний (pÚq)? 620. Эквиваленция высказываний (p«q) ложна. Что можно сказать о логическом значении строгой дизъюнкции этих высказываний (p Ú q)? 621. Импликация высказываний (p®q) ложна. Что можно сказать о логическом значении импликации (q®p) этих же высказываний? 622. Строгая дизъюнкция высказываний (p Ú q) ложна. Что можно сказать о логическом значении импликации этих высказываний (p®q)? 623. Строгая дизъюнкция высказываний (p Ú q) ложна. Что можно сказать о логическом значении эквиваленции этих высказываний (p«q)? 624. Эквиваленция высказываний (p«q) истинна. Что можно сказать о логическом значении строгой дизъюнкции этих высказываний (p Ú q)? 625. Строгая дизъюнкция высказываний (p Ú q) истинна. Что можно сказать о логическом значении конъюнкции этих высказываний (pÙq)? 626. Пусть значение высказывания p«q есть И. Что можно сказать о значении высказывания ( 627. Пусть значение высказывания p«q есть И. Что можно сказать о значении высказывания p« В №№ 646 – 655 определите значение истинности следующих выражений: 646. (ИÙИÙИ)®И; 647. (ИÙИÙЛ)®И;
649. (ИÚЛ)«(ИÙЛÙИ); 650. (((ИÚЛ)ÙЛ)®И)ÚЛ; 651. (((И®Л)®И)®И)®Л; 652. ((Л®И)«Л)®(ИÙЛ); 653. (И®Л)« 654. И Ú (ЛÙИÙИ); 655. Л Ú (ИÚИÚЛ). В №№ 656 – 665 определите логические значения следующих высказываний, не составляя полных таблиц истинности: 656. p®(q® r), где p - ложно; 657. pÚ(q® r), где p - истинно; 658. (pÙqÙr)® r, где p - ложно; 659. (pÙq)®(p Ú r), где q - ложно; 660. (p®q)«( 661. 662. ( 663. ( 664. (qÙr)®(pÚr),где p - истинно;
В №№ 666 – 675 высказывания p, q, r имеют соответственно значение истинности – И, Л, Л; определите значения следующих высказываний: 666. (pÙq)®(r®(sÚt)); 667. (p« 668. (pÙq)®(r«s); 669. p«(q®(r Ú s)); 670. (p Ú r)«(pÚs); 671. p®(q Ú r); 672. p®(r®s); 673. r®(pÚs); 674. pÙ(qÚr); 675. (p Ú q)Ùr.
676. (pÚqÚr)«s 677. (pÙs) Ú (qÚr) 678. (q®r)®(sÙp) 679. (q®p)®(r®s) 680. (qÚp)®(rÚs) 681. (qÙ(pÚr))«(rÙ 682. (rÙ(s«p))®(( 683. (qÙ 684. (rÙs)®(p®( 685. ((pÚ В №№ 686 – 705 приведите примеры рассуждений в соответствии со следующими формулами и проверьте табличным способом, являются ли они тождественно-истинными высказываниями: 686. (pÙq)®((qÙp)Úr) 687. (pÙq)®(pÚr) 688. (pÙq)®(qÚr) 689. (qÙp)®(q®(pÙq)) 690. ((p®q)Ù(p®r))®(p®(qÙr)) 691. ((p®q)Ù(r®s))®(p®(qÙr)) 692. ((p®q)Ù(q®r))®(p®r) 693. ((p®q)Ù(r®q))®((pÚr)®q) 694. (pÚq)®((qÚp)Ú(pÙr)) 695. (pÚq)®( 696. (p«q)®((q«p)Ú r) 697. (p«q)®((p®q)Ú r) 698. (p«q)®((q®p)Ú r) 699. ((p®q)Ù(q®p))®((p«q)Úr)
702. ((p®q)Ùq)®(pÚr) 703. ((p®q)Ù 704. (rÙ(p Ú q))®((
В №№ 706 – 775 определите табличным способом, к какому классу (всегда истинные, всегда ложные, нейтральные) относятся следующие формулы:
706. (p®q) 707. (
709. (pÚr)®(qÙ 710. p Ú (
711. (
713. (p®r)®(((q®r)®(pÚq))®r) 714. (p®q)®((p®r)®(p®(qÙr)))
717. (r®(p«q)) Ú 718. (p®q)«(
720. ((pÚq)Ù((rÚq)®q))®q 721. (p«q)®((q«r)®(p«r)) 722. (p®(q®p))Úq 723. q®(p®(qÚr)) 724. p®(pÚq) 725. (p®(qÙr))®(( 726. (p®q)®((p®r)®(p®(qÙr))) 727. (p®r)®((q®r)®((pÚq)®r)) 728. ((pÙq)®r)«((pÙ 729. ((p®q)Ù(p«r))®(qÙ 730. ((p®q)Ù(r® s))Ù(( 731. ((p®q)«( 732. ((pÚq)® r)®((pÚr)® 733. (( 734. (p Ú q)Ú( 735. ((p®q)®(p®r))«(
737. ((( 738. ((p®q)Ùr)Ú(
744. (r®( 745. (p«q) Ú ( 746. (pÙq)®(qÙp) 747. (pÙq)®p 748. (pÙq)®q 749. p®(q®(pÙq)) 750. ((p®q)Ù(p®r))®(p®(qÙr)) 751. ((p®q)Ù(r®s))®(p®(qÙr)) 752. ((p®q)Ù(q®r))®(p®r) 753. ((p®q)Ù(r®q))®((pÚr)®q) 754. (pÚq)®(qÚp) 755. (pÚq)®( 756. (p«q)® (q «p) 757. (p«q)® (p®q) 758. (p«q)® (q®p) 759. ((p®q)Ù(q®p))® (p«q)
762. ((p®q) Ùq)®p 763. ((p®q) Ù 764. (p Ú q)®((
766. (( 767. (( 768. (p®q)Ù (q Ú p)Ù(q®p)Ù(rÚsÚt) 769. ((q®p)Ù(p«q))Ú (q®p)Ù (p®q)Ú((rÚs)Ùt) 770. (( 771. (p®q)Ù(p Ú q)Ù(p«q)Ù(q®p)Ù(pÙrÙsÙt) 772. ( 773. (pÚr)Ù(sÚt)Ù(tÚp)Ù(p«r)Ù(sÚp)Ù(t®r)Ù(r Ú p) 774. (r®s)Ù(pÚqÚr)Ù(t®r)Ù(s Ú t)Ù(tÙ 775. (p®q)Ù(r®s)Ù(s®t)Ù(rÙ В №№ 776 – 795 с помощью таблицы истинности установите, являются ли равносильными суждения а) и б):
776. А) Сын работает на заводе, а дочь учится в школе. Б) Неверно, что сын не работает на заводе или дочь не учится в школе. 777. А) Иван и Петр друг друга не любят. Б) Неверно, что Иван любит Петра, и Петр любит Ивана. 778. А) Каждый студент этого факультета способен и трудолюбив. Б) Неверно, что каждый студент этого факультета неспособен и нетрудолюбив. 779. А) Прямоугольные треугольники бывают равнобедренными или неравнобедренными. Б) Неверно, что прямоугольные треугольники бывают равнобедренными и неравнобедренными. 780. А) Иван либо сын, либо внук Петра. Б) Неверно, что Иван сын Петра тогда и только тогда, когда является его внуком. 781. А) Если слово ставится в начале предложения, то оно пишется с большой буквы. Б) Неверно, что слово ставиться в начале предложения и при этом не пишется с большой буквы. 782. А) Если по проводнику проходит электрический ток, то вокруг проводника возникает магнитное поле. Б) Если вокруг проводника возникает магнитное поле, то по проводнику проходит электрический ток. 783. А) Число является тогда и только тогда четным, если оно делится на два. Б) Если число четное, то оно делится на два, а если число не четное, то оно не делится на два. 784. А) Человек нечестен и несправедлив. Б) Неверно, что если человек нечестен, то он справедлив. 785. А) На улице темно и сыро. Б) Неверно, что на улице темно или не сыро. 786. А) Я получаю стипендию тогда и только тогда, когда сдаю экзамены. Б) Я не получаю стипендию тогда и только тогда, когда не сдаю экзамены. 787. А) Я либо читаю книгу, либо иду в кино. Б) Я либо не читаю книгу, либо не иду в кино. 788. А) Я тогда и только тогда иду в кино, когда не читаю книгу. Б) Либо я иду в кино, либо читаю книгу. 789. А) Либо я не читаю книгу, либо я хочу прилечь. Б) Тогда и только тогда я читаю книгу, когда хочу прилечь. 790. А) Если будет хорошая погода, то мы отправимся в путешествие. Б) Не будет хорошей погоды, или мы не отправимся в путешествие. 791. А) Я учусь в институте или не работаю на заводе. Б) Если я работаю на заводе, то учусь в институте. 792. А) Тогда и только тогда мы отправимся в путешествие, когда будет хорошая погода. Б) Будет хорошая погода, и мы отправимся в путешествие, или не будет хорошей погоды, и мы не отправимся в путешествие. 793. А) Неверно, что тогда и только тогда мы отправимся в путешествие, когда будет хорошая погода. Б) Будет хорошая погода, но мы не отправимся в путешествие, или не будет хорошей погоды, а мы отправимся в путешествие. 794. А) Либо я увлекаюсь гимнастикой, либо плаванием. Б) Я увлекаюсь гимнастикой, но не увлекаюсь плаванием, или я не увлекаюсь гимнастикой, а увлекаюсь плаванием. 795. А) Неверно, что либо я увлекаюсь гимнастикой, либо плаванием. Б) Я увлекаюсь гимнастикой и плаванием, или я не увлекаюсь ни гимнастикой, ни плаванием. В №№ 796 – 805 определите, справедливы ли следующие равносильности:
796. ( 797. ( 798. (p®q)Ù(p«q)Ù(q®p)Ùp = pÙq
800. (p®q)Ù(p Ú q)ÙpÙ ( 801. (pÙ
В №№ 806 – 815 используя закон двойного отрицания, сформулируйте суждения, значения которых были бы эквивалентны следующим: 806. Наш факультет занял первое место в легкоатлетическом соревновании. 807. России чужда политика захвата чужих территорий. 808. Янка Купала - народный поэт Белоруссии. 809. Неверно, что гонка вооружений не обостряет международной напряженности. 810. Неверно, что капитализм не знает ни кризисов, ни безработицы. 811. Человек может отправиться в космический полет. 812. Субъект суждения распределен. 813. В озеро Байкал впадает множество рек. 814. Систематичность в работе лежит в основе успехов этого студента. 815. Тиберий обещал матери вернуться героем. В №№ 816 – 825 используя законы противоречия и исключения третьего, на основании данного суждения постройте тождественно-ложные и тождественно-истинные высказывания: 816. Наш факультет занял первое место в легкоатлетическом соревн
|
|||||||||||
|
Последнее изменение этой страницы: 2016-12-15; просмотров: 1506; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.222.56.251 (0.01 с.) |

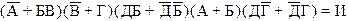


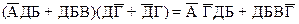
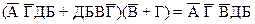
 стало быть в библиотеке были только студенты Дмитриев и Борисов.
стало быть в библиотеке были только студенты Дмитриев и Борисов.
 Ùq)«(pÚ
Ùq)«(pÚ  )?
)? Ù B) ® (
Ù B) ® ( ? 633. Пусть значение высказывания А Ú В есть Л. Что можно сказать о значении высказывания
? 633. Пусть значение высказывания А Ú В есть Л. Что можно сказать о значении высказывания  648. ((ИÙЛ)Ú(Л®И)Ú(ЛÚИ))®(ЛÙИÙИ);
648. ((ИÙЛ)Ú(Л®И)Ú(ЛÚИ))®(ЛÙИÙИ); ;
; 665. (
665. ( В заданиях №№ 676 – 685 необходимо определить истинностные значения каждого из следующих сложных высказываний, предположив, что простым высказываниям p, q, r и s соответственно даны значения И, Л, Л и И:
В заданиях №№ 676 – 685 необходимо определить истинностные значения каждого из следующих сложных высказываний, предположив, что простым высказываниям p, q, r и s соответственно даны значения И, Л, Л и И: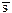 )
) 700. (pÚq)«((
700. (pÚq)«(( 701. (pÙq)«((
701. (pÙq)«(( 705. (p Ú q)®((p«q)Úr)
705. (p Ú q)®((p«q)Úr)
 708. (
708. ( )
)
 716. (p®qÙ(r Ú s)«(p®s)
716. (p®qÙ(r Ú s)«(p®s) )®
)®  )®(
)®( 736. ((pÙq)®r) Ú ((qÙp)®(r Ú s))
736. ((pÙq)®r) Ú ((qÙp)®(r Ú s)) 739. (p®q) Ú ((pÙ
739. (p®q) Ú ((pÙ  741. ((p®q)Ù(p®r))«(p®(qÙr))
741. ((p®q)Ù(p®r))«(p®(qÙr)) 743. (p®q)®((q®r)®(p® r))
743. (p®q)®((q®r)®(p® r)) 760. (pÚq)«(
760. (pÚq)«( 761. (pÙq)«(
761. (pÙq)«( 765. (p Ú q)®(p«q)
765. (p Ú q)®(p«q) Ùs)Ú(
Ùs)Ú( 799. (
799. (




