Интерпретация логических операций на диаграммах Эйлера-Венна и контактных схемах

Графически логические операции принято интерпретировать двумя основными способами:

1) на диаграммах Эйлера-Венна;

2) на контактных схемах.

 

Чтобы пользоваться диаграммами, необходимо иметь в виду, что дизъюнкция интерпретируется как объединение кругов, конъюнкция – как их пересечение, отрицание – как дополнение, логическая константа И – как универсальное множество, логическая константа Л – как пустое множество.

Проиллюстрируем с помощью диаграмм Эйлера-Венна законы поглощения (23) и (24) (рис. 12):

 

pÙ(pÚq) = p pÚ(pÙq) = p

 

 

 

Рис. 12

 

Законы исключения констант и удаления переменных (рис. 13):

 

pÙИ = p pÚЛ = p pÚИ = И pÙЛ = Л

 

p p p p

 

Рис. 13

 

Законы противоречия и исключения третьего (рис. 14):

 

pÚ = И pÙ = Л

 

 

Рис. 14

В начале ХХ века знаменитый австро-русско-голландский физик Пауль Эренфест (1880 – 1933), проектируя по заказу одной компании телефонный коммутатор, обнаружил, что законы логики легко продемонстрировать, используя контактные схемы.

Контактная схема – это устройство из проводников и двухпозиционных контактов. Контакты могут быть замыкающими или размыкающими. Каждый контакт подключен к переключателю. Участок цепи проводит ток, если все подключенные замыкающие контакты замкнуты, а размыкающие контакты разомкнуты. Участок цепи не проводит ток, если замыкающие контакты разомкнуты, а размыкающие контакты замкнуты.

На схеме каждому переключателю соответствует своя переменная. Все замыкающие контакты обозначаются соответствующими символами (p, q, …), а размыкающие этими же символами с отрицанием (, , …). Это означает, что при срабатывании переключателя р все его замыкающие контакты р проводят ток и им соответствует логическое значение И, а все размыкающие контакты не проводят ток и им соответствует Л. При отключении переключателя создается противоположная ситуация. Токопроводящий участок цепи эквивалентен логической константе И: · ·, непроводящий – Л: · ·

Состояние электрических устройств с той точки зрения, могут ли они проводить в данный момент электрический ток при соединении этих устройств с источником тока или не могут, можно охарактеризовать с помощью логических союзов.

Последовательное соединение контактов равнозначно конъюнкции. Конъюнкция истинна тогда и только тогда, когда все конъюнкты истинны, т.е. сигнал будет идти тогда и только тогда, когда все контакты замкнуты (рис. 15):

p q

 

· · · pÙq

 

Рис. 15

 

Параллельное соединение контактов равнозначно дизъюнкции (рис. 16):

p

· ·

q

· ·

pÚq

Рис. 16

 

Две параллельных ветви, в которых сигнал проходит, когда либо оба контакта замкнуты, либо оба разомкнуты, соответствуют эквиваленции (рис. 17 стр. 59):

p q

· · · ·

p«q

· · · ·

 

Рис. 17

 

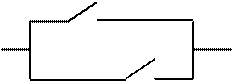
Две параллельных ветви, в которых противоположный контакту p контакт q разомкнут, если данный замкнут, и наоборот, – это строгая дизъюнкция (рис. 18):

 

p

· · · ·

p Ú q

q

· · · ·

Рис. 18