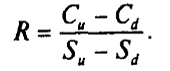Биноминальный метод оценки стоимости опционов

Биномиальная модель (binomial model) оценки "истинной", или внутренней (теоретической), цены опциона в текущий момент (t = 0) строится на простейшем допущении о поведении цены исходного актива. Биномиальная модель иногда называется по фамилиям предложивших ее авторов: моделью Кокса — Росса — Рубинштейна (Сох — Ross —Rubinstein). Представление модели обычно строится для европейского опциона, который может быть исполнен в день погашения. Если в качестве актива рассматривается акция, то предполагается, что дивиденд по ней не выплачивается в течение срока действия опциона. Для каждого периода времени существуют только две возможности движения цены актива: вверх до значения S_u (up) или вниз до значения S. Предполагается известной
вероятность изменения цены:

Цена опциона выводится методом формирования такого портфеля из исходных активов, доступных инвестору на рынке, который обеспечивал бы такой же денежный поток инвестору, что и колл-опцион. На рынке инвестору доступны исходный актив, на который создается право покупки (рассматривается колл-опцион), и безрисковые варианты инвестирования и займа. В результате арбитражных операций на совершенном рынке активы и портфели активов будут оцениваться по прогнозируемому денежному потоку и риску, связанному с получением этих потоков. Строя портфель с денежными потоками, как по опциону, можно утверждать, что цена опциона равна оценке портфеля. В противном случае инвестор получит арбитражный доход, покупая относительно дешевый альтернативный портфель и продавая относительно дорогой.

Портфель должен воспроизводить характеристики колл-опциона (денежные потоки и риск). Построить этот портфель можно, например, из исходных активов и безрисковых облигаций.

Цена колл зависит от цены исходного актива. Пусть при цене актива S _и цена опциона равна С _и в момент tI, а при цене актива S_d цена опциона С_d.

Портфель включает: 1) безрисковые облигации в денежном выражении В (цена облигации на количество облигаций); 2) покупку исходных активов в количестве R. Это количество покупаемых активов определяется из соотношения

Так как для однопериодного действия опциона, когда известны цены актива будущего периода, можно рассчитать цену опциона на конец периода t=1, то может быть найден портфель (определено число покупаемых исходных активов и число безрисковых облигаций). Портфель создается для каждого временного периода (для каждого периода в модели определяются значения R t и B t), что позволяет рассчитать его оценку и соответственно оценку опциона (текущую оценку опциона как актива, генерирующего денежные потоки на каждом временном промежутке). Конечным результатом итеративного процесса расчета оценки опциона будет оценка портфеля для I = О, составленного из К исходных активов и В безрисковых ценных бумаг. Если полученное значение К < О, то это означает продажу активов и ссужение денег. Если В < О, то это означает продажу безрисковой облигации или получение ссуды по безрисковой процентной ставке.

Цена колл (оценка опциона) = Текущая цена актива х R — Привлечение денежных средств для покупки активов = S х R — В.

Например, рассмотрим колл-опцион с ценой исполнения 50 долл. и сроком опциона два года. Текущая цена акции — 50 долл. Дивиденды не выплачиваются, и исполнить опцион можно только в конце второго года (рассматривается европейский опцион)1. Известны следующие значения цены акции по двум годам:

Для каждого года построим портфель, комбинируя R_t акций и привлекая B_t денежных средств для получения такого же денежного потока, какой генерирует опцион колл с ценой исполнения 50 долл. Итеративный процесс начинается с последнего года до исполнения опциона и доходит до года t = 1.

Построим портфель года t = 2, если цена акции поднимется до 70 долл. Денежные потоки по колл-опциону имеют вид:

Оценка колл совпадает с оценкой портфеля при равенстве денежных потоков:

100 х R₂₁ – (1+k_f) x B₂₁ = 50,

50 x R₂₁ – (1+k_f) x B₂₁ = 0

При k_f = 11% решение системы уравнений относительно R₂₁ и B₂₁ дает следующие значения: R₂₁ = 1, B₂₁ = 45. Если цена акции в году t = 1 равна 70 долл., то при займе 45 долл. и покупке одной акции инвестор получит такой же денежный поток, что и при покупке опциона колл. Цена колл на момент t = 1, если цена акции 70 долл., равна 70 х R₂₁ – В₂₁ = 25 долл. Если в момент t = 1 цена акции равна 35 долл., денежные потоки по опциону имеют вид:

находим, что для построения портфеля с таким же потоком, что и колл-опцион, нужно купить 0,71 акции и занять 22,5 долл. Оценка колл равна 0,71 х 50 - 22,5 = 13,2. Таким образом, в колл-опционе с ценой исполнения 50 долл. и сроком два года при рассмотренных допущениях о возможных ценах акции цена опциона равна 13,2 долл. [].

Модель Блэка-Шоулза

Модель ценообразования опционов Блэка-Шоулза (Black-Scholes Option Model — ОРМ), разработанная для оценки колл опционов, может использоваться для оценки всех производных бумаг, включая варранты, кон­вертируемые ценные бумаги, и даже для оценки собствен­ного капитала финансово зависимых фирм.

Модель основывается на следующих предположениях:

1) по базисному активу колл опциона дивиденды не выплачиваются в течение всего срока действия опциона;

2) нет трансакционных затрат, связанных с покупкой или продажей акции или опциона;

3) краткосрочная безрис­ковая процентная ставка известна и является постоянной в течение всего срока действия опциона;

4) любой поку­патель ценной бумаги может получать ссуды по краткос­рочной безрисковой ставке для оплаты любой части ее цены;

5) короткая продажа разрешается без ограничений, при этом продавец получит немедленно всю наличную сумму за проданную без покрытия ценную бумагу по се­годняшней цене;

6) колл-опцион может быть исполнен только в момент истечения опциона;

7) торговля ценными бумагами ведется непрерывно, и цена акции движется непрерывно и случайным образом.

Вывод OPM основывается на концепции безрискового хеджа: покупая акции и одновременно продавая колл опционы на акции, инвестор может конструировать без­рисковую позицию, где прибыли по акциям будут точно компенсировать убытки по опционам, и наоборот. Безрис­ковая хеджевая позиция должна приносить доход по став­ке, равной безрисковой процентной ставке:

 

 

 

 

где V - текущая стоимость колл опциона в момент t до истечения срока опциона; E - текущая цена базисной акции; N(d₁) - вероятность того, что отклонение будет меньше d₁, в условиях стандартного нормального распре­деления и, таким образом, N(d₁) и N(d₂) ограничивают область значений для функции стандартного нормального распределения; X - цена исполнения опциона; a_RF - без­рисковая процентная ставка; t — время до истечения сро­ка опциона - период опциона; 𝞼² - вариация доходности базисной акции.

Пример. Рассмотрим ситуацию, характерную для аме­риканского рынка. В качестве безрисковой ставки можно использовать доходность по казначейским векселям со сроком, равным сроку действия опциона. Вариация цены акции может быть оценена вычислением вариации отно­сительного изменения стоимости акции по дням в тече­ние последнего гола. Пусть E = 20 руб., X = 20 руб., t = 3 месяца, или 0.25 года, a_RF = 12%, или 0.12, 𝞼² = 0.16.

Используя вышеизложенные формулы, подсчитываем d₁ =0,25, d₁=0,05. N(d₁) = N(0,25), N(d₁) = N(0,05) оп­ределяем, используя таблицы функции стандартного нор­мального распределения, приведенные в приложении. На­ходим, что величине d₁ = 0,25 соответствует вероятность N(0,25)= 0,5000 + 0,0987 (из таблицы) = 0,5987; d₂ = 0,05 => N(0,05) = 0,5000+ 0,0199 (из таблицы) = 0,5199. Далее по первой формуле: V = 20 руб. • 0,5987 - 20 руб. • ехр (-0.12 • 0,25) • 0,5199 = 1.88 руб.

Равновесная рыночная стоимость опциона в рассматри­ваемых условиях составляет 1,88 руб.

Модель ОРМ определяет влияние пяти факторов на текущую стоимость опциона следующим образом: 1) сто­имость опциона возрастает с ростом цены акции, но с меньшим темпом; 2) если цена исполнения возрастает, то стоимость опциона снижается, но абсолютное измене­ние ее меньше; 3) если период действия опциона возра­стает, то возрастает и его стоимость; 4) при возрастании безрисковой процентной ставки стоимость опциона возра­стает незначительно; 5) с увеличением вариации цены базисного актива стоимость опциона увеличивается.