
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Вычисление координат точек разомкнутого теодолитного ходаСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
3.1.1 Уравнивание угловых измерений Уравнивание – это процесс математической обработки, в результате которой вычисляется и распределяется невязка. Разность между суммой измеренных углов и теоретической суммой называется угловой невязкой хода и обозначается f b.
Угловая невязка хода f b вычисляется по формуле:
где åbизм– сумма измеренных углов хода; åbтеор – теоретическая сумма углов. Теоретическая сумма углов вычисляется по формулам в зависимости от геометрии хода. Для разомкнутого теодолитного хода теоретическая сумма углов вычисляется: для измеренных горизонтальных углов правых по ходу
(у нас правые горизонтальные углы) для измеренных горизонтальных углов левых по ходу
где aН – дирекционный угол начальной стороны; aК – дирекционный угол конечной стороны; N – некоторое целое число, n – число измеренных углов. Вычисленная угловая невязка f b сравнивается с допустимой f b доп
где n – число измеренных углов. Сравниваются фактическая и допустимая невязки. Если вычисленная невязка f b больше допустимой f b доп, то необходимо все пересчитать. Если
Сумма всех поправок в углы должна равняться невязке f b с противоположным знаком.
Вычисляются исправленные углы:
Контроль уравнивания угловых измерений: сумма исправленных горизонтальных углов равна теоретической сумме
Таблица 2 Ведомость вычисления координат точек теодолитного хода (для примера. А красным обозначены данные, которые студент берет из таблицы и вставляет в свою ведомость)
åbизм = 757°48¢; fX = –0,08; fY = –0,16; åD Х теор = –331,16; åbтеор =221°14¢ – 183° 27¢ +180°´4 = 757° 47¢; f b = +1¢; допустимая
Пример вычисления угловой невязки (все вычисления, приведенные в примерах, показаны в «Ведомости вычисления координат точек теодолитного хода» табл. 2): Сумма измеренных углов равна
Теоретическая сумма углов правых по ходу равна
Угловая невязка
Допустимая угловая невязка вычисляется по формуле:
В примере перед корнем 1 минута. Для студентов 2 минуты. Вычисленная угловая невязка f b меньше допустимой f bдоп. Угловая невязка распределяется с обратным знаком на один угол, т.е. поправка равна минус 1 минута. Предпочтение имеют углы, у которых стороны короче. Вычисление исправленных углов:
Контроль уравнивания углов:
Сумма исправленных углов равна теоретической сумме åbтеор. Контроль получился. 3.1.2 Вычисление дирекционных углов
По известному дирекционному углу исходной стороны А-1(a А-1) и по исправленным углам b вычисляются дирекционные углы остальных сторон теодолитного хода по формулам:
Для горизонтальных углов левых по ходу формула вычисления дирекционных углов имеет вид:
Контроль вычисления дирекционных углов: в результате вычислений в разомкнутом теодолитном ходе получается дирекционный угол конечной стороны. Пример вычисления дирекционных угловL
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-12-27; просмотров: 3857; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.12.148.140 (0.01 с.) |

 ,
, ,
, ;
; ,
, , то вычисленная угловая невязка распределяется на измеренные углы поровну (но не меньше, чем точность отсчитывания или 0,5¢) с противоположным знаком, т.е.
, то вычисленная угловая невязка распределяется на измеренные углы поровну (но не меньше, чем точность отсчитывания или 0,5¢) с противоположным знаком, т.е.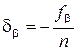 .
. .
. .
. ; åD Y теор = -206,68;
; åD Y теор = -206,68; ; f относит =1/2211 f допуст =1/2000
; f относит =1/2211 f допуст =1/2000 .
. .
. .
. .
. .
. .
.
 – дирекционный угол последующей стороны равен дирекционному углу предыдущей стороны плюс 180° и минус исправленный угол правый по ходу. Если результат получился больше 360°, то из результата необходимо вычесть 360°.
– дирекционный угол последующей стороны равен дирекционному углу предыдущей стороны плюс 180° и минус исправленный угол правый по ходу. Если результат получился больше 360°, то из результата необходимо вычесть 360°. .
. .
. ;
; ;
; .
.


