
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Определение прямоугольных координат точек теодолитного ходаСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
ФЕДЕРАЛЬНОЕ АГЕНСТВО ПО ОБРАЗОВАНИЮ РОССИЙСКОЙ ФЕДЕРАЦИИ РОССИЙСКИЙ ГОСУДАРСТВЕННЫЙ ГЕОЛОГОРАЗВЕДОЧНЫЙ УНИВЕРСИТЕТ Имени Серго Орджоникидзе Кафедра РМСВМС и маркшейдерского дела С.И.Чекалин «СОСТАВЛЕНИЕ ТОПОГРАФИЧЕСКОГО ПЛАНА» Геодезия: Топографические съемки Учебное пособие по геодезиидля студентов 1-го курса групп ПГ и РФ
Москва, 2010
© С.И.Чекалин. «Составление топографического плана». Геодезия: Топографические съемки. - Учебное пособие по геодезии для студентов 1-го курса групп ПГ, РФ. - М.: РГГРУ, 2010, 40 с.
Рассмотрены вопросы, связанные с обработкой результатов полевых измерений для составления топографического плана местности: азимутальная привязка замкнутого теодолитных хода; обработка и уравнивание результатов угловых измерений; обработка ведомостей координат и высот теодолитного хода и оценка точности построения съемочного обоснования; обработка результатов полевых измерений тахеометрической и горизонтальной съемки; составление топографического плана. Пособие предназначено для студентов 1 курса, геологических, инженерно-геологических и геофизических специальностей (ПГ и РФ). В качестве примера обработки полевых геодезических данных пособием могут пользоваться студенты других специальностей, изучающих дисциплину «геодезия» и «основы топографии».
Российский государственный геологоразведочный университет имени Серго Орджоникижзе © Кафедра РМСВМС и маркшейдерского дела Тираж 100 экз. Печ. л. 2,5
Оглавление
Введение Топографические планы масштабов 1:5000, 1:2000, 1:1000 и 1:500 используются на различных стадиях строительства и эксплуатации инженерно-технических сооружений, при разведке и промышленном освоении месторождений полезных ископаемых, при решении специальных инженерно-геодезических задач и др. Для стадии проектирования выполняют топографическую съемку в необходимом для работы масштабе, либо обновляют (пополняют) уже имеющиеся топографические материалы (геоподосновы) ранних лет издания. Топографическая съемка ведется в плановой местной или общегосударственной системе координат с привязкой съемочного обоснования (теодолитных ходов) к имеющейся сети геодезических пунктов, координаты которых выдаются соответствующими организациями. Высоты точек местности определяют обычно в Балтийской системе высот. При топографической съемке местности в указанных выше масштабах объектами съемки являются: рельеф местности (с установленной высотой сечения); границы ситуации (леса, луга, пашни, и т.п.); положение и границы гидрографии (ручьи, реки, озера, пруды и т.п.) и инженерно-технические сооружения на ней (мосты, плотины и т.п.); линейные сооружения (дороги, эстакады и др.); линии связи (ЛЭП, телефон и др.); подземные и наземные линии коммуникаций; населенные пункты (их границы, дома с пристройками и др.); отдельные местные предметы и выдающиеся инженерные сооружения, которые могут иметь и значение ориентиров (церкви, башни, трубы, отдельные деревья, отдельные камни и пр.). Целью настоящего учебного пособия является ознакомление с принципами обработки результатов измерений, выполненных в теодолитных ходах, а также с обработкой результатов топографической съемки и составлением по ним топографического плана заданного масштаба. В учебном пособии приведены результаты топографической съемки местности на площади порядка 2 га (примерно 140 х 140 м). В качестве съемочного обоснования проложен замкнутыйтеодолитный ход, одной из вершин которого является пункт Государственной геодезической сети. Исходные данные в работе приведены по вариантам, закрепляемым за каждым студентом. В качестве примера обработки данных полевых измерений рассматриваются результаты измерений для варианта № 36. Особенности обработки данных топографической съемки разъяснены в соответствующих разделах настоящего учебного пособия. Дополнительно об этом можно посмотреть в учебниках по геодезии [1, 2 ], а также в лекциях по геодезии в теме «Топографические съемки».
Исходные данные
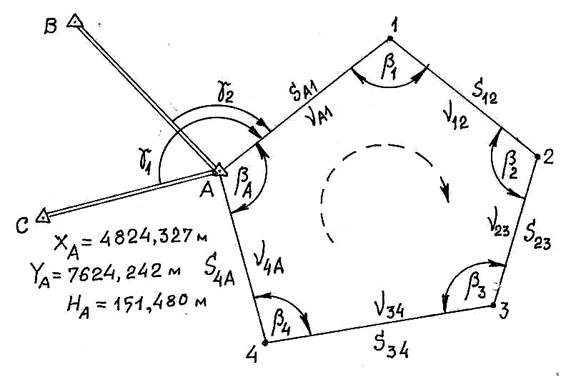
Для топографической съемки местности на площади примерно 2 га проложен замкнутый теодолитный ход (А -1-2-3-4- А) – рис. 1, опирающийся на два исходных направления (АВ и АС).
Рис. 1. Схема теодолитного хода - - - -→ - направление хода
В качестве опорных точек (для азимутальной, плановой и высотной привязок) использованы пункты Государственной геодезической сети (ГГС): А - пункт IV класса, В - пункт III класса, С - пункт сети 2-го разряда. Прямоугольные координаты указанных пунктов В и С приведены в приложении 1. Прямоугольные координаты пункта А, а также его абсолютная высота указаны для всех вариантов непосредственно на рис. 1. Для азимутальной привязки теодолитного хода в вершинах В и С измерены примычные углы g1 и g2. Значения указанных примычных углов даны вприложении 1. В замкнутом теодолитном ходе (при движении по часовой стрелке) получены значения правых по ходу горизонтальных углов bА, b1, b2, b3, b4. Значениягоризонтальных углов представлены в приложении 2. Для всех линий теодолитного хода измерены наклонные расстояния S А1, S 12 и т.д. и соответствующие углы наклона nА1, n12 и т.д. В приложении 3 даны величины наклонных расстояний, являющиеся их средними арифметическими значениями, полученными при измерениях длин линий на местности в прямом и обратном направлениях. Углы наклона, знаки которых соответствуют выбранным выше направлениям ходов, приведены в приложении 4. Указанные углы наклона также являются средними арифметическими значениями измеренных углов в прямом и обратном направлениях со знаком прямого соответствующего угла. Со всех точек теодолитного хода, в том числе и с точки А Государственной геодезической сети, выполнена тахеометрическая съемка, результаты которой представлены в приложении 5 и на абрисах тахеометрической съемки (приложение 6). Абрис горизонтальной съемки ситуации также приведен в приложении 6. Обычно бригада геодезистов выполняет измерения на местности и их обработку практически в любой удобной для них последовательности. Вам же предлагается сравнительно строгая последовательность обработки данных, определяемая, в основном, учебными целями. Все исходные данные одного варианта взаимосвязаны между собой, поэтому будьте особенно внимательны при выборе исходных данных именно Вашего варианта!
Таблица 1 Пример 1. Решение обратной геодезической задачи. Вычисление дирекционных углов исходных направлений Дирекционный угол aВА DXА = 4824,327 – 4963,815 = - 139,488 м DYА = 7624,242 – 6135,633 = +1488,609 м (II четверть). rВА = arctg 1488,609 / 139,488 = arctg 10,6719503 = 84о38´49´´ aВА = 180о - rВА = 180о - 84о38´49´´= 95о21´11´´ aАВ = 95о21´11´´+ 180о = 275о21´11´´ Дирекционный угол aСА DXА = 4824,327 – 6241,087 = - 1416,760 м DYА = 7624,242 – 7332,708 = +291,534 м (II четверть). rСА = arctg 291,534 / 1416,760 = arctg 0,20577515 = 11о37´40´´ aСА = 180о - rСА = 180о - 11о378´40´´= 168о22´20´´ aАС = 168о22´20´´+ 180о = 348о22´20´´.
Дирекционные углы исходных направлений используются для азимутальной привязки замкнутого теодолитного хода.
2.2. Азимутальная привязка теодолитного хода
Азимутальная привязка заключается в передаче дирекционных углов исходных направлений на одну или несколько линий теодолитного хода. В соответствии со схемой замкнутого теодолитного хода, приведенной на рис. 1, для его привязки измерены два примычных угла g в точке А. Результатом азимутальной привязки должно получиться значение дирекционного угла линии А -1 (aА1). Известна взаимосвязь между дирекционными углами и горизонтальными углами, измеренными на местности: an + 1 = an ± 180o ± b, (4) где (+ b) - для левых по ходу горизонтальных углов; (- b) - для правых по ходу горизонтальных углов. Напомним,что в формуле (4) при 180о всегда можно ставить знак «плюс», а значение дирекционного угла следует приводить к полному кругу Так, в соответствии со схемой рис.1, aА1 (ВА) = aВА + 180o + g2 (5) aА1(СА) = aСА + 180o + g1 Разница в полученных значениях дирекционных углов не должна превышать 1¢, т.е. aА1(ВА) - aА1(СА) £ 1' (6) Если условие (6) не выполняется, то: 1.Помните, что 1о = 60¢, а не 100¢, как, возможно, Вы посчитали. 2.Проверьте Ваши исходные данные. 3.Еще раз вычислите дирекционные углы исходных направлений. Если условие (6) выполнено, то вычисляют среднее значение дирекционного угла, которое и будет в дальнейших расчетах являться исходным: aА1 = 0,5 (aА1(ВА) + aА1(СА)) (7)
Пример 2. Азимутальная привязка линии А-1. aА1(BА) = 95о21´11´´ + 180o + 168о36´18´´= 83о57´29´´ aА1(CА) = 168о22´20´´+ 180o + 95о34´30´´= 83о56´50´´ Условие (6) выполнено (разность дирекционных углов не превышает одной минуты). aА1 = 0,5(83о57´29´´ + 83о56´50´´) = 83о57´09´´. 2.3.Обработка результатов угловых измерений Все последующие результаты обработки приводятся в ведомостикоординат точек теодолитного хода, форма которой и пример заполнения и обработки приведены в табл. 2. Предварительно в ведомость координат необходимо занести следующие данные: 1. Координаты точек А, В и С (приложение 1; рис. 1); 2. Дирекционные углы направлений В-А, С-А, aА1(BА), aА1(CА) и aА1 с учетом использованных в расчетах примычных углов (данные азимутальной привязки – решение обратных геодезических задач); 3. Измеренные внутренние (правые по ходу) горизонтальные углы в вершинах А, 1, 2, 3, 4 теодолитного хода (приложение 2). Как уже указывалось выше, замкнутый теодолитный ход имеет внутренний контроль, в частности, по сумме внешних или внутренних горизонтальных углов, независимо от результатов привязки к исходным направлениям. åbВНЕШН.(ТЕОР.) = 180о (n + 2), (8) åbВНУТР.(ТЕОР.) = 180о (n - 2), (9) где n - число углов (вершин) многоугольника. Величина угловой невязки fb при этом определяется по формуле fb = åbВНЕШН. - 180о (n + 2), (10) fb = åbВНУТР. - 180о (n - 2). (11) В формулах (10) и (11) используются, естественно, суммы практически измеренных горизонтальных углов. Величина угловой невязки fb не должна превышать по абсолютной величине допустимую угловую невязку fb ДОП, вычисляемую по формуле fb ДОП = ±1¢ где n - число измеренных горизонтальных углов. Следовательно, качество угловых измерений определяется выполнением условия: fb £ fb доп (13) Качество угловых измерений определяется выполнением условия (13) по вычисленной по формуле (12) величине допустимой угловой невязки. Если в расчетах допущены ошибки, то условие (13) не выполнится. В этом случае: проверьте Ваши исходные данные; проверьте арифметические действия при суммировании углов. Результаты вычислений занести в табл. 2. Пример 3. Оценка точности результатов угловых измерений в замкнутом ходе. åbВНУТР = 540о01´06´´ åbТЕОР = 180о (n - 2) = 540о00´00´´ fb = 540о01´06´´ - 540о00´00´´= + 1´06´´ = + 66´´
Условие (13) выполнено. Ведомость координат
2.4.Вычисление дирекционных углов линий теодолитного хода
Общая последовательность обработки в указанном разделе заключается в исправлении (уравнивании) измеренных горизонтальных углов и затем вычислении дирекционных углов линий теодолитного хода. Поправки в измеренные горизонтальные углы вычисляют по формуле vb = - fb / n (14) где n - число измеренных горизонтальных углов. Исправленные горизонтальные углы определяют как алгебраическую сумму измеренного угла и поправки: bi ИСПР = bi + vb i (15) При исправлении углов следует придерживаться выполнения следующих условий. 1.Величина поправки округляется до 1¢¢. 2. Сумма всех поправок должна быть равна невязке с обратным знаком vb = - fb (16) Таблица 2 Точек теодолитного хода
3.Поправку необходимо распределить примерно поровну на все углы, чтобы вся невязка без остатка была израсходована на поправки. 4.Поправки большей величины, полученные при округлениях, следует вводить в горизонтальные углы, образованные короткими сторонами. åbi ИСПР.ВНЕШН. = 180о (n + 2) (17) åbi ИСПР.ВНУТР. = 180о (n - 2) (18) Посмотрите алгоритм уравнивания горизонтальных углов в ведомости координат (табл. 2). Вычисление дирекционных углов производится последовательно от линии к линии по формулам a12 = aА1 + 180о - b1 ИСПР a23 = a12 + 180о - b2 ИСПР (19) a34 = a23 + 180о - b3 ИСПР Контроль вычисления дирекционных углов выполняется по формуле aА1 = a4А + 180о - bА ИСПР. (20) Пример 5. Вычисление горизонтальных проложений d А1 = 67,537 cos (-5о06,8¢) = 67,268 м d 12 = 96,322 cos (+3о08,9¢) = 96,177 м и т.д.
2.6.Оценка точности теодолитных ходов Для каждой из линий теодолитного хода вычисляют приращения координат DХ и DY конечной ее точки по выбранному направлению хода по отношению к начальной. Например, для линии MN по направлению M-N DX N = d MN cos aMN DY N = d MN sin aMN (23) где d MN - горизонтальное проложение линии MN; aMN - дирекционный угол направления M- N. Значения приращений координат округляют до 0,001 м. При последовательном переходе от начальной исходной точки к конечной теоретически должно выполняться условие по осям X и Y: å DC ТЕОР = XK - XH å DU ТЕОР = UK - UH (24) где å DC ТЕОР и å DU ТЕОР - суммы приращений координат по всему ходу; (н) и (к) - характеризуют координаты начальной и конечной точек разомкнутого теодолитного хода. Поскольку в замкнутом теодолитном ходе XH = XK и YH = YK, то теоретические суммы приращений координат, вычисленные по формуле (24), должны быть равны нулю: åDC ТЕОР = О; åDU ТЕОР = О (25) В этом случае и невязки в приращениях координат определяются суммами fx = å DC ВЫЧ; fy = å DU ВЫЧ (26)
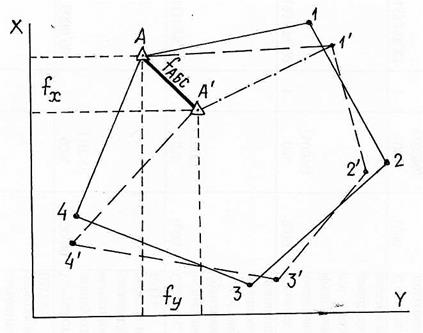
Рис. 3. Физический смысл линейной невязки хода.
На рис. 3 показан физический смысл невязок fх и fy. Поскольку при измерениях возникают погрешности в результате действия многочисленных факторов, то при перемещении по фактическому ходу конечная точка хода может оказаться в другом положении, отличном от идеального. Расхождение в положениях фактической и идеальной точек хода характеризуется абсолютной (линейной) невязкой fАБС, проекции которой на оси X и Y и определяют величины невязок fХ и fУ. При этом очевидно, что
Отношение абсолютной невязки к периметру хода (в данном случае - к его длине, определяемой суммой горизонтальных проложений) дает значение относительной невязки fОТН = fАБС / å d = 1 / (å d: fабс), (28) являющейся характеристикой точности теодолитного хода. Полученная величина относительной невязки сравнивается с допустимой ее величиной, при этом качество теодолитного хода определяется выполнением условия fОТН £ fОТН ДОП (29) Величина fОТН ДОП определяется соответствующими инструкциями по производству работ обычно в пределах 1: 1000 - 1: 3000 в зависимости от сложности местности. В Вашем задании предусматривается значение fОТН.ДОП = 1: 1500 Данные расчетов занести в ведомость координат (табл. 2). Если условие (29) не выполняется, то необходимо обратить внимание на следующие моменты: 1. Суммировать приращения координат в замкнутом теодолитном ходе можно только по линиям А-1, 1-2, 2-3, 3-А. 2. Возможно, что неверно вычислена невязка fабс. 3. Проверьте вычисления приращений координат. Пример 6. Оценка точности замкнутого теодолитного хода. å DC ВЫЧ = fx = - 0,065 м å DU ВЫЧ = fy = - 0,024 м fАБС = 0,069 м å d = 363,225 м fОТН = 1 / (363,225: 0,069) = 1: 5240 < 1: 1500. Условие (29) выполнено. Рекомендации к поиску вероятных ошибок в измерениях и вычислениях при обработке ведомости координат
Конечная оценка точности теодолитного хода производится на основе всех (линейных и угловых) измерений, выполненных при создании съемочного обоснования. Кроме того, оценке точности теодолитного хода предшествует и большой объем вычислений, что, даже несмотря на ряд контрольных вычислений, повышает вероятность ошибки, в результате чего условие (29) может не выполниться. Чаще всего отступление от неравенства (29) сравнительно небольшое, что как раз и затрудняет поиск ошибок. Грубые погрешности находятся сравнительно быстро и легко. В некоторых случаях, если небольшие погрешности допущены в двух или нескольких линиях (в углах или расстояниях), то отыскание их только в камеральных условиях чаще всего не представляется возможным. Необходимы повторные измерения, которые обычно начинают с самых сложных участков. Если же погрешности были допущены только в одной линии (в ее длине или ее направлении), то поиск их может быть сравнительно легко осуществлен по величинам и знакам невязок fx и fy в приращениях координат. Для этого предварительно определяют дирекционный угол линейной невязки fАБС, по той же схеме, как это Вы выполняли при решении обратной геодезической задачи (см. п. 2.1): rf = arctg (fy / fx) ® (табл. 1) ® af (30) Затем следует образовать группы дирекционных углов: А) -- совпадающих с направлением невязки af ± 180o; Б) -- перпендикулярных к направлению невязки (af + 90o) ± 180o. Если погрешность допущена в длине линии, то наиболее вероятно, что она присутствует в тех линиях, для которых их направление (дирекционный угол) совпадает с направлением невязки (сравнение производится по группе А). Так, например, в соответствии с рис. 3, наиболее вероятна погрешность в длине линии 1-2, либо линии 3-4 теодолитного хода. Если погрешность допущена в направлении линии, то наибольшая вероятность этого для тех линий, дирекционные углы которых отличаются от направления невязки на 90о. (Сравнение производится по группе В). Таким образом, наиболее вероятна погрешность в направлении линии 2-3, но имеется и вероятность в ошибках направлений в линиях А -1 и 4- А. В том случае, если указанный алгоритм поиска погрешностей не даст результатов, то следует ожидать, что погрешности присутствуют в двух или более линиях. Это требует повторения полевых измерений, перед которыми необходимо еще раз внимательно выверить полевые журналы предшест-вующих работ, а также повторно проверить все вычисления. Повторные полевые измерения целесообразно начинать с проверки длин линий и их горизонтальных проложений (при этом в первую очередь проверяют наибо-лее сложные для измерений участки). Проверку горизонтальных углов также начинают с вершин, наблюдения с которых по каким-либо причинам выполнялись с большими помехами: видимость соседних пунктов была недостаточной, производилась перестановка вех и т.п. Пример 7. Поиск вероятных погрешностей в теодолитных ходах. Рассмотрим результаты обработки данных, приведенные в табл. 2. (На самом деле невязки в ходах допустимы, в связи с чем нет необходимости в поиске погрешностей. Пример далее дается только в учебных целях для пояснения алгоритма поиска погрешностей). rf = arctg (0,024 / 0,065)» 20,3о (III-я четверть) ® af» 200,3o.
Для анализа здесь можно использовать только дирекционные углы по замкнутому теодолитному ходу. Самым близкими по величине в группе А является дирекционный угол линии 4- А (»3,5о), то есть можно ожидать, что имеется погрешность в длине линии 4- А. Погрешность в направлении более всего ожидается в линии 3-4 (сравните дирекционный угол невязки по группе В и самой линии 3-4).
2.7. Исправление приращений координат Данная работа производится только при выполнении условия (29) Поправки в приращения координат определяют по формулам: vx i = - d i (fx / å d) vyi = - d i (fy / å d), (31) т.е. они пропорциональны величинам горизонтальных проложений, использованных при вычислении соответствующего значения приращения координат. Примечания: 1. Величину поправки следует округлить до 0,001 м. 2. При введении поправок необходимо соблюдать равенства: å νХ = -fX; å νY = - fY. (32) Исправление приращений координат производят арифметическим сложением их вычисленных значений и соответствующих им поправок: DC i ИСПР = DC i ВЫЧ + vx i DU i ИСПР = DU i ВЫЧ + vy i (33) Контролем исправления является выполнение следующего условия: å DC ИСПР = О å DU ИСПР = О (34) В правой части выражений (34) - теоретические значения сумм приращений координат. Пример 8. Исправление приращений координат. vx 1 = - 67,268 ((-0,065): 363,225) = + 0,012 м и т. д. vy 1 = - 67,268 (- 0,024: 363,225) = + 0,005 м и т. д. Следует отметить, что из-за малой величины невязки fy при округлении значения поправок могут оказаться меньше 0,001 м. В этих случаях поправки вводят в приращения координат, полученные по самым большим горизонтальным проложениям (как это и сделано в ведомости координат для рассматриваемого примера). Условие (32) выполнено. å DC ИСПР = О; å DU ИСПР = О Условие (34) выполнено.
2.8. Вычисление координат точек теодолитного хода Координаты точек хода вычисляют последовательно по ходу А- 1-2-3-4- А: ХА ® X1 ® X2 ® X3® X4; YА ® Y1 ® Y2 ® Y 3 ® Y 4 (35) с использованием формул Х1 = ХА + DХ1 ИСПР; Y1 = YА + DY1 ИСПР Х2 = Х1 + DХ2 ИСПР; Y2 = Y1 + DY2 ИСПР и т д. (36) Контролем вычислений является равенство координат точки А: ХА = Х4 + DХА ИСПР; YА = Y4 + DYА ИСПР (37) их исходным значениям: ХА ВЫЧ = ХА ИСХ; YА ВЫЧ = YА ИСХ (38) При невыполнении условия (38) обратите внимание на указания, приведенные в выделенном абзаце раздела 2.7. Результаты вычислений записать в ведомость координат (табл. 2). Пример 9. Вычисление координат точек теодолитного хода. Х 1 = 4824,327+ (+7,099) = 4831,426 м Y 1 = 7624,242 + (+66,899) = 7691,141 м Х 2 = 4831,426 + (-86,309) = 4745,117 м и т. д. Y 2 = 7691,141 + (+42,406) = 7733,547 м и т. д. Контроль: Х А= 4759,310+(+65,017) = 4824,327 м; Y А=7620,301+(+3,941) = 7624,242 м. Условие (38) выполнено.
3. Определение высот точек теодолитного хода Цель работы – получить навыки в обработке ведомости высот замкнутого теодолитного хода. Конечный результат – абсолютные высоты точек 1, 2, 3, 4. Для высотной привязки используется значение абсолютной высоты пункта А Государственной геодезической сети, приведенное на рис. 1. Для передачи высот с точки на точку по каждой линии теодолитного хода на местности были получены в прямом ходе углы наклона, значения которых приведены в приложении 4 (Вы их уже использовали при определении горизонтальных проложений).
3.1. Вычисление превышений и оценка качества высотного хода
Превышение hM последующей точки M линии относительно предыдущей N определяется по формуле hM = d NM tg nNM, (39) где d NM - горизонтальное проложение линии MN (горизонтальные проложения у Вас уже вычислены и записаны в ведомости координат); nNM - угол наклона линии MN по направлению M-N. Имеющиеся у Вас исходные данные следует занести в соответствующую таблицу 3 (ведомость высот точек теодолитного хода). Контроль качества высотного хода производится на основе сравнения сумм превышений с их теоретическим значением по величине невязки в превышениях fh = Sh ВЫЧ - (Hк - Hн) (40) В формуле (40) Sh выч - сумма вычисленных превышений по четырем линиям теодолитного хода (А -1, 1-2, 2-3, 3-4, 4- А); Нк и Нн - абсолютные высоты конечной и начальной точек теодолитного хода (разность этих высот характеризует теоретическое значение суммы превышений – fh ТЕОР). Очевидно, что для замкнутого теодолитного хода теоретическое значение суммы превышений должно быть равно нулю, поскольку Нк = Нн, т.е. невязка в превышениях для замкнутого теодолитного хода определяется как сумма превышений, вычисленных по этому ходу: fh = Sh ВЫЧ (41) Величины полученных невязок сопоставляются со значением допустимой невязки, вычисляемой по формуле fh ДОП = ± (0,04 S d) / где S d - сумма горизонтальных проложений соответствующего теодолитного хода; n – число превышений (линий) теодолитного хода. Таким образом, условие fh ≤ fh ДОП (43) является характеристикой качества высотного хода Если условие (43) не выполнено, то: 1.Проверьте вычисления по формуле (39). 2. Посмотрите еще раз, правильно ли Вы учли знаки превышений при вычислении невязки по формуле (40). Таблица 3 Ведомость высот (пример 10)
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-06-19; просмотров: 1494; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.135.201.101 (0.01 с.) |

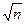 (12)
(12)
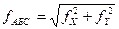 (27)
(27)


