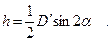Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Математическая обработка замкнутого теодолитного ходаСодержание книги
Поиск на нашем сайте
Целью математической обработки теодолитного хода является вычисление координат точек хода. Для решения этой задачи необходимы следующие исходные данные. 1. Измеренные теодолитом горизонтальные углы βi. 2. Измеренные и приведенные к горизонту длины сторон S 3. Координаты (X1, Y1) пункта ГГС точки Р1. 4. Дирекционный угол α0 с пункта P1на соседний пункт ГГС точку М и измеренный теодолитом примычный угол βпр. Весь процесс вычисления координат удобно разбить на отдельные этапы.
В замкнутом многоугольнике, каковым является рассматриваемый теодолитный ход, теоретически Σ βтеор = 180˚ (n – 2) Вследствие неизбежных погрешностей измерений на практике равенство (80) на будет выполняться. Поэтому Σ βi - 180˚ (n – 2) = fβ ≠ 0. Величина fβ называется угловой невязкой. Она служит показателем точности угловых измерений и должна удовлетворять допуску fβ ≤ fдоп.
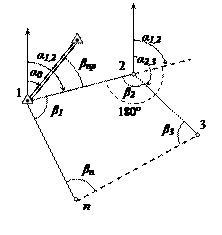
где п - количество углов в ходе, t - точность отсчетного устройства теодолита. Если невязка fβ не удовлетворяет допуску, то по-видимому, угловые измерения содержат грубую (одну или несколько) погрешность, которую необходимо выявить и устранить в результате повторных измерений. Если угловая невязка удовлетворяет допуску, то измерения углов выполнены удовлетворительно. Однако невязка fβ внесет в дальнейшие вычисления неоднозначность, поэтому ее следует устранить, введя в измеренные углы поправки vi = - fβ /n. Если невязка f β не делится без остатка на число углов n, то несколько большие поправки вводят в углы с короткими сторонами. Исправленные углы βi называются увязанными. Этап 2. Вычисление дирекционных углов сторон Для вычисления координат точек хода необходимо знать дирекционные углы сторон. Из рис.8.3 следует, что дирекционный угол α1,2 стороны Р12 равен α1,2 = α0 + βпр Продолжим сторону Р12 и отметим при точке 2 угол α1,2. Очевидно, что следующий дирекционный угол α2,3 равен α2,3 = α1,2 + 180˚ - β2. Рассуждая аналогично, можно написать
С целью контроля еще раз вычисляют α1,2 α1,2 = αп,1 + 180˚ - β1. Найденный α1,2 должен быть равен α1,2. Найденные по формуле дирекционные углы верны для так называемых правых углов βi. Если по ходу нумерации точек теодолитного хода измеренные углы расположены слева, то они называются левыми. Для таких углов формулы дирекционных углов имеют вид αi, i +1 = αi -1, i - 180˚ + βi. Этап 3. Вычисление и увязывание приращений координат
Представим стороны теодолитного хода векторами. Известно, что сумма векторов в замкнутом многоугольнике, а также суммы их проекций на координатные оси, равны нулю, т.е.
Вследствие погрешностей в измеренных длинах сторон теоретические равенства для вычисленных Δ Xвыч = S · cos α и Δ Yвыч = S · cos α выполняться не будут.
Величины fX и fY называются невязками. Они являются.в основном показателями точности линейных измерений. Образование невязок fX, fY графически означает незамыкание хода. Отрезок F = P′1Pназывается абсолютной линейной невязкой. Очевидно, что
Погрешность линейных измерений принято характеризовать относительной погрешностью, на которую накладывается допуск
где Р – периметр хода (сумма длин всех сторон). Если допуск не выполняется, то в линейных измерениях допущена одна или несколько грубых погрешностей, которые необходимо выявить и устранить в результате повторных измерений длин линий. Если допуск выполняется, то невязки fX и fY следует распределить с противоположным знаком между всеми Δ Х и Δ Y пропорционально длинам сторон. С учетом введенных поправок приращения координат называются исправленными или увязанными. Этап 4. Вычисление координат точек хода Поскольку координаты точки P1 (Х1, Y1) известны, то X2 = X1 + Δ X1,2 испр ; Y2 = Y1 + Δ Y1,2 испр ; X3 = X2 + Δ X2,3 испр ; Y3 = Y2 + Δ Y2,3 испр ; ……………………………………………… Xn = Xn-1 + Δ Xn -1, n испр ; Yn = Yn-1 + Δ Yn -1, n испр ; X1 = Xn + Δ Xn ,1 испр ; Y1 = Yn + Δ Yn ,1 испр ; Вычисления в последнем равенстве выполняют с целью контроля. 34. Сущность тахеометрической съемки. Обработка результатов, построение плана. Тахеометрическая съемка - это планово-высотная съемка, в результате которой получают топографический план местности. Основой съемки являются теодолитные ходы, по точкам которых проложены нивелирные ходы. Нивелирные ходы могут быть выполнены способами геометрического или тригонометрического нивелирования. Формально тахеометрическую съемку можно разделить на плановую (съемку контуров) и высотную (съемку рельефа). Плановая съемка ведется полярным способом. Высотная съемка выполняется способом тригонометрического нивелирования. Фактически же обе съемки производятся совместно, в результате чего определяются пространственные координаты снимаемой точки. Полевые работы. Тахеометрическая съемка выполняется обычным теодолитом, например, 2Т30, и комплектом из двух-трех реек. Съемка ведется с точек теодолитного хода, называемых станциями. Перед началом съемки теодолит на станции приводят в рабочее положение, выполняя следующие три операции: 1) центрирование; 2) приведение оси вращения теодолита в отвесное положение; 3) ориентирование.
Попутно с выбором реечных точек ведут схематический чертеж их - абрис. На абрисе стрелками указывают направление скатов. В дальнейшем при рисовке топографического плана линии скатов, показанные стрелками, будут использованы для решения задачи интерполирования по нахождению точек горизонталей, как стороны и диагонали квадратов при нивелировании поверхности. Для каждой реечной точки i на станции производятся следующие измерения: 1) βi - полярный горизонтальный угол; 2) Di - наклонное расстояние, взятое по нитяному дальномеру; 3) αi - вертикальный, угол взятый при наведении средней нити сетки на отсчет по рейке, равный высоте инструмента. На каждой станции в зависимости от сложности ситуации и рельефа может быть от одного до нескольких десятков реечных точек. Все выполненные измерения заносят в журнал тахеометрической съемки. Математическая и графическая обработка материалов. Математическая обработка заключается в вычислении для каждой реечной точки полярных координат β, d и высоты Н. Координата β берется непосредственно из измерений. Горизонтальное расстояние d вычисляется по формуле D = D′·cos2 α, a H = Hст +h, где Нст - высота станции; h - превышение реечной точки над станцией. Согласно формуле
Если вместо теодолита применяют тахеометры - автоматы, то значения d и h получают непосредственно в процессе измерений. Применение электронного тахеометра позволяет получать прямоугольные координаты реечных точек. В результате графической обработки материалов измерений и вычислений должен быть построен топографический план местности. Вначале на листе ватмана, как и в случае теодолитной съемки, строят координатную сетку и наносят по координатам точки теодолитного хода. Затем вокруг каждой станции наносят, используя полярные координаты, реечные точки. При этом полярные углы β удобно откладывать с помощью кругового транспортира. Подписывают номер и высоту каждой реечной точки. После этого, используя абрис, рисуют в условных топографических знаках ситуацию и рельеф в виде горизонталей. Завершающим этапом является оформление плана.
|
|||||||||||||||||||
|
Последнее изменение этой страницы: 2016-12-10; просмотров: 1067; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.15.239.50 (0.012 с.) |

 Этап 1. Уравнивание углов.
Этап 1. Уравнивание углов.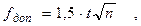
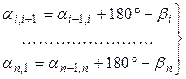
 При известных координатах точки P1, дирекционных углах всех сторон и их длинах можно, последовательно решая прямую геодезическую задачу, найти координаты всех точек хода. Однако, дело осложняется тем, что в измеренных длинах сторон содержатся погрешности. Это, как и в случае с углами, приведет к неоднозначности решения. Поэтому необходимо предварительно выполнить уравнивание приращений координат.
При известных координатах точки P1, дирекционных углах всех сторон и их длинах можно, последовательно решая прямую геодезическую задачу, найти координаты всех точек хода. Однако, дело осложняется тем, что в измеренных длинах сторон содержатся погрешности. Это, как и в случае с углами, приведет к неоднозначности решения. Поэтому необходимо предварительно выполнить уравнивание приращений координат.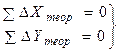

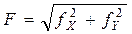
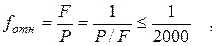
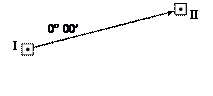 Первые две операции точно такие же, как и при измерении углов. Поскольку плановая часть тахеометрической съемки ведется полярным способом, то операция ориентирования связана с выбором и закреплением на местности полярной оси. Начало полярной системы уже выбрано - это точка стояния теодолита (станция). В качестве полярной оси можно выбрать любое известное направление на местности, например, северное направление магнитного меридиана. Наиболее удобно за полярную ось принять сторону теодолитного хода, исходящую из точки стояния. После выбора полярной оси ее необходимо инструментально закрепить, т.е. сориентировать лимб так, чтобы при наведении теодолита вдоль полярной оси (на соседнюю точку хода) отсчет по лимбу был 0˚ 00′.
Первые две операции точно такие же, как и при измерении углов. Поскольку плановая часть тахеометрической съемки ведется полярным способом, то операция ориентирования связана с выбором и закреплением на местности полярной оси. Начало полярной системы уже выбрано - это точка стояния теодолита (станция). В качестве полярной оси можно выбрать любое известное направление на местности, например, северное направление магнитного меридиана. Наиболее удобно за полярную ось принять сторону теодолитного хода, исходящую из точки стояния. После выбора полярной оси ее необходимо инструментально закрепить, т.е. сориентировать лимб так, чтобы при наведении теодолита вдоль полярной оси (на соседнюю точку хода) отсчет по лимбу был 0˚ 00′. После этого операция ориентирования считается законченной. Лимб же закрепляют и в процессе работы на станции он должен оставаться неподвижным. Съемку начинают с выбора на местности точек, подлежащих съемке. В эти точки будут устанавливаться рейки, поэтому они называются реечными. При выборе точек для съемки рельефа руководствуются, прежде всего, тем, чтобы между двумя соседними точками линию ската можно было считать равномерной. В этом случае реечные точки 1, 2, 3, 4 будут выбраны в местах перегиба рельефа. При протяженных равномерных скатах хотя бы двух точек было бы в принципе достаточно, фактически же их густота должна быть не ниже, чем это определено соответствующим нормативным документом. Обычно через 2 - 3 см в масштабе плана.
После этого операция ориентирования считается законченной. Лимб же закрепляют и в процессе работы на станции он должен оставаться неподвижным. Съемку начинают с выбора на местности точек, подлежащих съемке. В эти точки будут устанавливаться рейки, поэтому они называются реечными. При выборе точек для съемки рельефа руководствуются, прежде всего, тем, чтобы между двумя соседними точками линию ската можно было считать равномерной. В этом случае реечные точки 1, 2, 3, 4 будут выбраны в местах перегиба рельефа. При протяженных равномерных скатах хотя бы двух точек было бы в принципе достаточно, фактически же их густота должна быть не ниже, чем это определено соответствующим нормативным документом. Обычно через 2 - 3 см в масштабе плана.