
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Переход от значений румбов к дирекционным угламСодержание книги Поиск на нашем сайте
Пример 1. Решение обратной геодезической задачи. Вычисление дирекционных углов исходных направлений Дирекционный угол aВА DXА = 4824,327 – 4963,815 = - 139,488 м DYА = 7624,242 – 6135,633 = +1488,609 м (II четверть). rВА = arctg 1488,609 / 139,488 = arctg 10,6719503 = 84о38´49´´ aВА = 180о - rВА = 180о - 84о38´49´´= 95о21´11´´ aАВ = 95о21´11´´+ 180о = 275о21´11´´ Дирекционный угол aСА DXА = 4824,327 – 6241,087 = - 1416,760 м DYА = 7624,242 – 7332,708 = +291,534 м (II четверть). rСА = arctg 291,534 / 1416,760 = arctg 0,20577515 = 11о37´40´´ aСА = 180о - rСА = 180о - 11о378´40´´= 168о22´20´´ aАС = 168о22´20´´+ 180о = 348о22´20´´.
Дирекционные углы исходных направлений используются для азимутальной привязки замкнутого теодолитного хода.
2.2. Азимутальная привязка теодолитного хода
Азимутальная привязка заключается в передаче дирекционных углов исходных направлений на одну или несколько линий теодолитного хода. В соответствии со схемой замкнутого теодолитного хода, приведенной на рис. 1, для его привязки измерены два примычных угла g в точке А. Результатом азимутальной привязки должно получиться значение дирекционного угла линии А -1 (aА1). Известна взаимосвязь между дирекционными углами и горизонтальными углами, измеренными на местности: an + 1 = an ± 180o ± b, (4) где (+ b) - для левых по ходу горизонтальных углов; (- b) - для правых по ходу горизонтальных углов. Напомним,что в формуле (4) при 180о всегда можно ставить знак «плюс», а значение дирекционного угла следует приводить к полному кругу Так, в соответствии со схемой рис.1, aА1 (ВА) = aВА + 180o + g2 (5) aА1(СА) = aСА + 180o + g1 Разница в полученных значениях дирекционных углов не должна превышать 1¢, т.е. aА1(ВА) - aА1(СА) £ 1' (6) Если условие (6) не выполняется, то: 1.Помните, что 1о = 60¢, а не 100¢, как, возможно, Вы посчитали. 2.Проверьте Ваши исходные данные. 3.Еще раз вычислите дирекционные углы исходных направлений. Если условие (6) выполнено, то вычисляют среднее значение дирекционного угла, которое и будет в дальнейших расчетах являться исходным: aА1 = 0,5 (aА1(ВА) + aА1(СА)) (7)
Пример 2. Азимутальная привязка линии А-1. aА1(BА) = 95о21´11´´ + 180o + 168о36´18´´= 83о57´29´´ aА1(CА) = 168о22´20´´+ 180o + 95о34´30´´= 83о56´50´´ Условие (6) выполнено (разность дирекционных углов не превышает одной минуты). aА1 = 0,5(83о57´29´´ + 83о56´50´´) = 83о57´09´´. 2.3.Обработка результатов угловых измерений Все последующие результаты обработки приводятся в ведомостикоординат точек теодолитного хода, форма которой и пример заполнения и обработки приведены в табл. 2. Предварительно в ведомость координат необходимо занести следующие данные: 1. Координаты точек А, В и С (приложение 1; рис. 1); 2. Дирекционные углы направлений В-А, С-А, aА1(BА), aА1(CА) и aА1 с учетом использованных в расчетах примычных углов (данные азимутальной привязки – решение обратных геодезических задач); 3. Измеренные внутренние (правые по ходу) горизонтальные углы в вершинах А, 1, 2, 3, 4 теодолитного хода (приложение 2). Как уже указывалось выше, замкнутый теодолитный ход имеет внутренний контроль, в частности, по сумме внешних или внутренних горизонтальных углов, независимо от результатов привязки к исходным направлениям. åbВНЕШН.(ТЕОР.) = 180о (n + 2), (8) åbВНУТР.(ТЕОР.) = 180о (n - 2), (9) где n - число углов (вершин) многоугольника. Величина угловой невязки fb при этом определяется по формуле fb = åbВНЕШН. - 180о (n + 2), (10) fb = åbВНУТР. - 180о (n - 2). (11) В формулах (10) и (11) используются, естественно, суммы практически измеренных горизонтальных углов. Величина угловой невязки fb не должна превышать по абсолютной величине допустимую угловую невязку fb ДОП, вычисляемую по формуле fb ДОП = ±1¢ где n - число измеренных горизонтальных углов. Следовательно, качество угловых измерений определяется выполнением условия: fb £ fb доп (13) Качество угловых измерений определяется выполнением условия (13) по вычисленной по формуле (12) величине допустимой угловой невязки. Если в расчетах допущены ошибки, то условие (13) не выполнится. В этом случае: проверьте Ваши исходные данные; проверьте арифметические действия при суммировании углов. Результаты вычислений занести в табл. 2. Пример 3. Оценка точности результатов угловых измерений в замкнутом ходе. åbВНУТР = 540о01´06´´ åbТЕОР = 180о (n - 2) = 540о00´00´´ fb = 540о01´06´´ - 540о00´00´´= + 1´06´´ = + 66´´
Условие (13) выполнено. Ведомость координат
2.4.Вычисление дирекционных углов линий теодолитного хода
Общая последовательность обработки в указанном разделе заключается в исправлении (уравнивании) измеренных горизонтальных углов и затем вычислении дирекционных углов линий теодолитного хода. Поправки в измеренные горизонтальные углы вычисляют по формуле vb = - fb / n (14) где n - число измеренных горизонтальных углов. Исправленные горизонтальные углы определяют как алгебраическую сумму измеренного угла и поправки: bi ИСПР = bi + vb i (15) При исправлении углов следует придерживаться выполнения следующих условий. 1.Величина поправки округляется до 1¢¢. 2. Сумма всех поправок должна быть равна невязке с обратным знаком vb = - fb (16) Таблица 2 Точек теодолитного хода
3.Поправку необходимо распределить примерно поровну на все углы, чтобы вся невязка без остатка была израсходована на поправки. 4.Поправки большей величины, полученные при округлениях, следует вводить в горизонтальные углы, образованные короткими сторонами. åbi ИСПР.ВНЕШН. = 180о (n + 2) (17) åbi ИСПР.ВНУТР. = 180о (n - 2) (18) Посмотрите алгоритм уравнивания горизонтальных углов в ведомости координат (табл. 2). Вычисление дирекционных углов производится последовательно от линии к линии по формулам a12 = aА1 + 180о - b1 ИСПР a23 = a12 + 180о - b2 ИСПР (19) a34 = a23 + 180о - b3 ИСПР Контроль вычисления дирекционных углов выполняется по формуле aА1 = a4А + 180о - bА ИСПР. (20)
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-06-19; просмотров: 1469; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 13.59.114.66 (0.01 с.) |

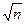 (12)
(12)



