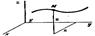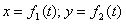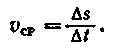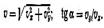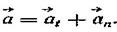Простые и сложные движения точки и твердого тела в кинематике. Основные параметры и уравнения движения.

Кинематика – это раздел механики, в котором изучается механическое движение материальных точек и твердых тел без учета причин, вызывающих эти движения. Кинематику часто называют геометрией движения.

Механическим движением называется изменение взаимного расположения тел
относительно друг друга в пространстве с течением времени. Любое механическое движение относительно.

Материальной точкой называется такое тело, размерами и формой которого можно пренебречь в сравнении с размерами других тел или расстояниями до них в условиях данной задачи.

В общем случае различные точки твердого тела совершают разные движения. Поэтому и возникает необходимость изучить в первую очередь движение отдельных точек тела. Чтобы определить положение точки в пространстве, нужно иметь какое-то неподвижное тело или связанную с ним систему координатных осей, которую называют системой отсчета. Движение заданного тела или точки обнаруживается только путем сравнения с системой отсчета.

В природе не существует неподвижных тел и, следовательно, не может быть абсолютно неподвижных систем отсчета. Обычно условно неподвижной системой отсчета считают систему координатных осей, связанную с Землей. Рассмотрим для примера движение точки в какой-то условно неподвижной системе координат xyz.

Положение точки М в пространстве определяется тремя координатами. Эти координаты изменяются при переходе точки в другое положение. Кривая, которую описывает точка при движении в пространстве относительно выбранной системы отсчета, называется ее траекторией.

Траектории делятся на прямолинейные (например, движение точек поршня двигателя) и криволинейные (круговые — движение точек шкива, круглой пилы; параболические — движение жидкости при истечении из отверстия в боковой стенке сосуда и др.).

Движение точки в пространстве прежде всего определяется скоростью, которая характеризует быстроту и направление движения точки в данный момент времени.

В зависимости от скорости движение точки может быть равномерным и неравномерным. При равномерном движении скорость постоянна по величине, при неравномерном — переменна. Изменение скорости во времени характеризуется ускорением. Скорость и ускорение точки являются векторными величинами.

При изучении движения точки необходимо различать два важных понятия: пройденный путь (или перемещение) и расстояние. Расстояние определяет положение точки на ее траектории и отсчитывается от некоторого начала отсчета. Расстояние является алгебраической величиной, так как в зависимости от положения точки относительно начала отсчета и от принятого направления оси расстояний оно может быть и положительным, и отрицательным. В отличие от расстояния путь, пройденный точкой, всегда определяется положительным числом. Путь совпадает с абсолютным значением расстояния только в том случае, когда движение точки начинается от начала отсчета и совершается по траектории в одном направлении.

Уравнения, определяющие положение движущейся точки в зависимости от времени, называются уравнениями движения. Наиболее удобный способ задания движения точки — естественный способ. При этом задается траектория точки (графически или аналитически) и закон движения точки по траектории.

Пусть произвольная точка А перемещается по заданной траектории. Принимая точку 0 за начало отсчета, уравнение движения можно представить в виде: s = f (t), где s — расстояние точки А от начала отсчета; t — время.

Положение движущейся в плоскости точки (рис.б) можно определить, если известны ее координаты х и у относительно системы двух взаимно перпендикулярных координатных осей Ох и Оу. При движении точки ее координаты изменяются с течением времени, следовательно, x и у являются некоторыми функциями времени и определяют движение точки:

Такой способ задания движения точки называется координатным. С помощью уравнений движения можно найти траекторию точки. Для этого из них нужно исключить параметр — время t — и найти зависимость между координатами точки у = f (х).

Рассмотрим некоторые основные определения, важные для последующего изложения. Если точка за равные промежутки времени проходит равные отрезки пути, то ее движение называется равномерным.

Скорость равномерного движения v измеряется отношением пути s, пройденного точкой за некоторый промежуток времени, к величине этого промежутка времени

Если известны проекции скорости на оси координат, можно определить ее значение и направление:

Изменение скорости в единицу времени определяется ускорением.

Найденное ускорение характеризует изменение численного значения скорости и ее направления. Для удобства ускорение раскладывают на взаимно перпендикулярные составляющие по касательной и нормали к траектории движения